3.2 Bir Rijit Cismin Kinematiği

Rijit cisim bir varsayımdır. Bu varsayım bir cismin hareketini incelememiz sırasında bize önemli kolaylıklar sağlayacaktır. Bunlar:

1. Bir rijit cismin düzlemsel hareketi o cisim üzerinde bulunan her hangi iki noktanın hareketi belirlendiğinde belirlenmiştir

   Bir cismin A ve B noktalarının zamana göre bulundukları konumlar biliniyor kabul edelim. Bu durumda hareketin her hangi bir t zamanında A ve B noktalarının konumu biliniyor demektir. S rijit cisim üzerinde her hangi bir başka nokta olduğunda, rijit cisim varsayımından dolayı AS ve BS uzunlukları sabit bilinen boyutlardır. A ve B noktalarının her hangi bir t anında konumları bilindiğinde, S noktasının konumuda belirlidir. Örneğin şekilde gösterilen rijit cisim üzerinde bulunan A, B ve S noktalarını ele alalım. Bir süre sonra A ve B noktaları A', B' konumuna gittiği biliniyor ise, AS ve BS uzunluklarının bilinen sabit uzunluklar olmasından dolayı S' noktasının konumu A' ve B' konumları ile tanımlıdır.

   Rijit cismin konumunu A ve B noktaları yerine cisim üzerinde sabitlenmiş A noktasından B noktasına uzanan bir AB vektörü ile de tanımlayabiliriz.

   AB vektörü rijit cisim üzerinde sabittir. B her hangi nokta olacağından AB vektör uzunluğu istenilen bir uzunluk seçilebilecektir. Bu durumda seçilmiş olan referans eksen takımına göre cismin konumu vektörün başlangıç noktası konumu (rijit cisim üzerinde bulunan A noktasının konumu) ve AB doğrusunun referans eksene göre açısal konumu ( 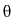açısı) ile belirlenebilir.

2. Rijit cisimlerde bir doğru üzerinde bulunan noktaların doğru yönünde hız bileşenleri eşit olmalıdır. Çünkü rijit cisim tanımından dolayı bu yönde uzama veya kısalma olmayacaktır ve iki nokta arasında uzaklık sabittir. A ve B noktaları arasında olası bir bağıl hareket mutlaka AB doğrusuna diktir.

V^'_A=V^'_B
3. Rijit cismin kinematiği ile ilgilendiğimizden dolayı, cismin fiziksel boyutları önemli değildir. Bu durumda cismin gerçek fiziksel boyutları unutularak cisim bir AB doğrusu veya basit bir geometrik şekil olarak gösterilebilir. Uzvun gerçek sınırları kinematik açıdan önemli olmadığından her bir uzuv sonsuz bir düzlem gibi kabul edilebilir ve bu düzlem kullanılmak istenilen her hangi bir noktayı içerir.

Düzlemsel hareket için belirtilmiş olan bu üç sonuç mekanizmaların kinematik analizi sırasında kullanılan çok önemli kavramlardır.

Bir başka önemli husus ise, cisimlerin üzerinde ele aldığımız noktaların gerçek cisimlerin üzerinde A, B, C gibi işaretli olmadığı, bu sembolleri bizim o noktaları ayırt etmek için koyduğumuzu unutmamamızdır. Birimizin A dediğine diğerimiz B der ise, bu gayet doğal olup kavga edilmesini gerektirmez (ancak kitapta devamlı olarak sabit uzva 1, giriş uzvuna 2 denmiş ise, veya giriş kolu mafsalları A₀ ve A olarak gösterilmiş ise, sizlerde tabii ki bu konuda ön yargılı olup benzer sayıları kullanacaksınız. Bu karşılıklı iletişimi kolaylaştırır ise de şart değildir). İstenir ise uzuvlar harflerle, ilgilendiğimiz noktalar ise sayılarla gösterilebilir.

©es