3.4 Mekanizmalarda Vektör Devreleri
Mekanizmalarda bulunan uzuvlar ile herhangi bir düzlemsel hareket yapan cisimler arasında en önemli fark, mekanizma uzuvları hareketlerini sınırlayan ve onları diğer uzuvlara bağlayan mafsallardan dolayı, girdi parametreleri değerlerine göre sınırlandırılmış bir hareket halindedirler. Birbirlerine mafsallar ile bağlı uzuvlar kapalı çokgenler oluşturacaklardır. Bu çokgenlerin her birine devre diyeceğiz. Hareket analizinde temel yaklaşımımızın başlangıç noktası bu devreleri matematiksel olarak ifade etmek olacaktır.
Kinematik analize başlarken her bir uzuvla ilgili tüm boyutları bildiğimizi kabul edeceğiz. Kinematik analiz sadece boyutlarını bildiğimiz (veya boyutlarını bir varsayım ile tahmin ettiğimiz) uzuvlardan oluşan bir mekanizma için yapılabilir. Genel olarak döner mafsal eksenleri arasında uzaklık veya bir döner mafsal orta nok-tasından aynı uzvun bağlandığı bir kayar mafsal eksenine olan dik uzaklık uzuv boyutlarıdır. Bazı durumlarda ise verilen boyutlar kullanılarak istenilen başka boyutların çıkarılması gerekebilir. Ancak her durumda, mekanizma uzuvları hakkında yeterli boyut bilgisinin olduğu kabul edilecektir.
Önceki kısımda, bir uzvun konumu için bu uzvun üzerinde iki noktanın konumunun bilinmesi gerektiğini ve bu iki noktanın konumu bilinir ise, başka her hangi bir noktanın konumunun bulanabileceğini göstermiştik. Bu durumda konum anali-zinde hedefimiz her bir uzuv üzerinde iki noktanın konumunu belirlemek olacaktır. Nokta sayısını azaltmak, bir uzvun konumunu belirlediğimizde diğer uzvun konumunun belirlenmesinde kolaylık sağlamak için bu noktaları uzuvlar arasında daima çakışan noktalar seçmek tercih edeceğimiz bir husus olacaktır. Bu şekilde uzuv konumlarını tanımlamak için gereken parametre sayısı azaltılabilecektir. Bir uzvun üzerinde tanımlayacağımız vektörün başlangıç noktası başka bir uzvun üzerinde tanımladığımız vektörün bitiş noktası olabilecektir.

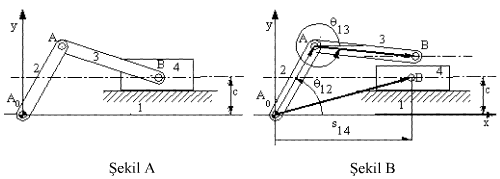
Bir örnek vermek için yukarıda gösterilen dört-çubuk mekanizmasını ele
alalım. Bu mekanizmada A0 ,1 ve 2 uzuvları üzerinde; A, 2 ve
3 uzuvları üzerinde; B, 3 ve 4 uzuvları üzerinde ve B0 , 4
ve 1 uzuvları üzerinde daima çakışan noktalardır. Bir an için Şekil B
de gösterildiği gibi daima çakışması gereken B3 ve B4
noktalarını birbirinden ayırdığımızı düşünelim. Bu durumda iki açık zincir
elde edilecektir (A0AB ve B0B). Bu açık zincirlerde
uzuv sayısı mekanizmada bulunan uzuv sayısı kadardır. Bu uzuvların açık
zincir durumunda konumlarını belirleyelim. Konumlarını belirlemek için
ilk olarak bir sabit referans ekseni seçmemiz gerekir. Her hangi bir referans
ekseni seçebilir isek de, eğer referans eksenimizin başlangıç noktası
A0 veya B0 dan geçer ise, ek sabit değerlere ihtiyacımız
olmayabilir. Örneğin eksen başlangıcını A0 olarak ve pozitif
x eksenini A0B0 yönünde seçer isek, elde edeceğimiz
ilişkilerin daha basit olacağı görülecektir (eğer başka her hangi bir
sabit referans ekseni seçilir ise, bu durumda seçim noktasına bağlı olarak
bir uzvun veya noktanın konumu belirlenirken 3 yeni sabit parametre denklemlerde
yer alacaktır). Şimdi seçmiş olduğumuz referans takımına göre 2 uzvunun
konumunu belirlemek istersek, 2 uzvu sabit uzva göre sadece dönme yapabileceğinden
ve A0 noktası 2 ve 1 uzuvları arasında daima çakışan nokta
olduğundan, dönme miktarını belirleyen ![]() 12
parametresi değerini belirlersek 2 uzvunun konumunu belirlemiş oluruz.
Eğer 2 uzvu üzerinde A noktasının yerini bulmak istersek A0A=a2
biliniyor kabul edildiğinden (uzuv boyutu), A noktasının koordinatları
A (a2cos
12
parametresi değerini belirlersek 2 uzvunun konumunu belirlemiş oluruz.
Eğer 2 uzvu üzerinde A noktasının yerini bulmak istersek A0A=a2
biliniyor kabul edildiğinden (uzuv boyutu), A noktasının koordinatları
A (a2cos![]() 12
, a2sin
12
, a2sin![]() 12
) olarak kolayca belirlenir (veya kutupsal olarak a2
12
) olarak kolayca belirlenir (veya kutupsal olarak a2![]()
![]() 12).
A noktası 2 ve 3 noktaları üzerinde çakışan noktalar olduğundan 3 uzvunun
konumunun belirlenmesi sırasında A noktası zaten
12).
A noktası 2 ve 3 noktaları üzerinde çakışan noktalar olduğundan 3 uzvunun
konumunun belirlenmesi sırasında A noktası zaten ![]() 12
parametresi ile bilindiğinden, şimdi 3 uzvunun konumunu belirlemek için
sadece
12
parametresi ile bilindiğinden, şimdi 3 uzvunun konumunu belirlemek için
sadece ![]() 13
parametresini belirlememiz yeterli olacaktır. Benzer bir şekilde 4 uzvunun
konumunu belirlemek için
13
parametresini belirlememiz yeterli olacaktır. Benzer bir şekilde 4 uzvunun
konumunu belirlemek için ![]() 14
parametresinin belirlenmesi yeterlidir. Bu şekilde elde ettiğimiz açık
kinematik zincirde bütün uzuvların konumlarının belirlenmesi üç parametre
gerekmektedir (
14
parametresinin belirlenmesi yeterlidir. Bu şekilde elde ettiğimiz açık
kinematik zincirde bütün uzuvların konumlarının belirlenmesi üç parametre
gerekmektedir (![]() 12
,
12
, ![]() 13
ve
13
ve ![]() 14
). Görüldüğü gibi bu parametreler mutlaka mafsal serbestlik derecelerine
aittir.
14
). Görüldüğü gibi bu parametreler mutlaka mafsal serbestlik derecelerine
aittir.
Her uzuv bir vektor ile gösterilebildiğine göre, bu vektörlerin başlangıç
ve bitiş noktalarını mekanizmada daimi çakışan noktalar olarak seçelim
ve 2 uzvu için A0A, 3 uzvu için AB, 1 uzvu için
A0B0 ve 4 uzvu için AB vektörlerini
tanımlayalım. Mekanizmamızda sadece döner mafsallar olduğu için değişken
parametreler açı parametreleri olup bu vektörlerin boyutları (şiddeti)
sabit uzuv boyutlarıdır (A0A=a2, AB=a3,
A0B0=a1 ve B0B=a4)
ve bu vektörlerin yönleri (A0B0 sabit vektörü
hariç) değişken açı parametreleri (![]() 12
,
12
, ![]() 13
ve
13
ve ![]() 14
) ile tanımlanır. Açık zincir olarak ele alındığında, bu üç parametreye
verilen değerlere bağlı olarak B3 ve B4 noktaları
farklı konumlarda olacaktır (ve bu sistemin serbestlik derecesi 3 dür).
B noktasının konumu:
14
) ile tanımlanır. Açık zincir olarak ele alındığında, bu üç parametreye
verilen değerlere bağlı olarak B3 ve B4 noktaları
farklı konumlarda olacaktır (ve bu sistemin serbestlik derecesi 3 dür).
B noktasının konumu:
A0A +AB=A0B3 (1,2,3 açık zinciri
için)
A0B0 +B0B= A0B4
(1,4 açık zinciri için)
Ancak biliyoruz ki mekanizmada B noktası 3 ve 4 uzuvları üzerinde daima çakışan iki noktadır. Öyle ise her iki zincirden ayrı ayrı elde edilen A0B3 ve A0B4 vektörleri daima çakışan iki noktayı gösterdiklerinden birbirlerine eşit olmaları gerekir (A0B3 = A0B4). Bu değerlendirme ile:
A0A +AB=A0B0 +B0B
Vektör denklemi elde edilir. B noktası daima çakışan nokta olduğundan
bu denklem mekanizmanın alabileceği her konum için geçerli olması şarttır.
Aksi durumda mekanizmayı oluşturan zincir kopmuştur (mekanizma yoktur).
Şekilden görüleceği gibi, dört-çubuk mekanizmasında bir kapalı devre
vardır ve bu kapalı devreyi gösteren bir vektör denklemi elde edilmiştir.
Bu denklem bize oluşan zincirin kapalı bir zincir olduğunu gösterir (daima
çakışan noktalar). Bu denkleme devre kapalılık denklemi veya vektör
devre denklemi diyeceğiz. Bu denklem bir vektör denklemi olup denklemdeki
değişkenler mutlaka mekanizmadaki mafsalların serbestlik dereceleri ile
ilişkilidir. Bir vektör denkleminden iki skaler denklem elde edileceğinden,
iki parametre değeri bu denklemler kullanılarak çözülebilir. Devre kapalılık
denklemimizde üç parametre (![]() 12,
12,
![]() 13
ve
13
ve ![]() 14)
olduğuna göre, eğer bu parametrelerden birisi tanımlanmış ise (
14)
olduğuna göre, eğer bu parametrelerden birisi tanımlanmış ise (![]() 12
olsun) diğer iki parametre (
12
olsun) diğer iki parametre (![]() 13
ve
13
ve ![]() 14)
bu vektör devre denkleminden çözülebilmelidir. Tanımlanması gereken parametre
sayısı mekanizmanın serbestlik derecesine eşittir. Dikkat edilecek husus,
bu parametreler arasında ilişki basit lineer bir ilişki olmayıp trigonemetrik
fonksiyonları içeren karmaşık bir ilişkidir. Bu parametrelere konum
değişkenleri diyeceğiz.
14)
bu vektör devre denkleminden çözülebilmelidir. Tanımlanması gereken parametre
sayısı mekanizmanın serbestlik derecesine eşittir. Dikkat edilecek husus,
bu parametreler arasında ilişki basit lineer bir ilişki olmayıp trigonemetrik
fonksiyonları içeren karmaşık bir ilişkidir. Bu parametrelere konum
değişkenleri diyeceğiz.
Devre kapalılık denkleminde bulunan vektörleri göstermenin bir kolay
yolu ise her bir vektörü kompleks sayı kullanarak tanımlamaktır. Örneğin
A0A vektörünün uzunluğu a2 ve yatay eksenle yaptığı
açı ![]() 12
olduğuna göre:
12
olduğuna göre:
A0A = a2cos![]() 12+
ia2sin
12+
ia2sin![]() 12
12
veya Euler formülü kullanılarak üstel fonksiyon olarak:
A0A = a2![]()
yazılabilir. Benzer bir şekilde, uzuv boyutları ai olarak ( a1=
A0B0 , a2= A0A, ve benzeri.)
gösterilir ise, vektör devre denklemi kompleks sayılar ile:
a2![]() +a3
+a3![]() =a1+a4
=a1+a4![]()
olarak yazılabilir. İstendiğinde bu vektörler x ve y bileşenleri kullanılarak
da yazılabilir. Bu durumda dört-çubuk mekanizması için vektör devre denklemi:
a2cos![]() 12+a3cosq
12+a3cosq![]() 13=a1+a4cos
13=a1+a4cos![]() 14
14
a2sin![]() 12+a3sinq
12+a3sinq![]() 13=a4sin
13=a4sin![]() 14
14
Dört-çubuk mekanizması için vektörlerin boyutları sabit olup açısal yönleri değişkendir. Serbestlik derecesi tanımına tekrar göz atarsak, tanımlanması gereken parametre sayısı mekanizmanın tahrik edildiği mafsala ait olup serbestlik derecesi kadar parametre tanımlanmalıdır. Bu parametreler dört-çubuk mekanizmasında olduğu gibi daima açısal parametre olması gerekmez.
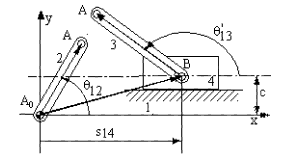
Farklı bir basit örnek olarak Şekil A da görülen krank-biyel mekanizmasını
ele alalım. B noktasında 3 ve 4 uzuvlarını birbirine bağlayan döner mafsalı
söktüğümüzü düşünelim (Şekil B). dört uzvu için yapmış olduğumuz incelemeye
benzer bir inceleme yaptığımızda A0AB zincirinde bulunan 2
ve 3 uzuvlarının konumları seçmiş olduğumuz referans eksenlerine göre
![]() 12
ve
12
ve ![]() 13
açısal konum parametrelerinin tanımlanması ile belirlenebilir. 4 uzvunun
konumu ise, 1 uzvuna göre kayar çift ekseni yönünde öteleme yapacağından,
kayar çift ekseni yönünde tanımlanan s14
konum değişkeni ile belirlenir. Bu konum değişkeni öteleme değişkenidir.
Bu durumda elde edilen devre kapalılık denklemi:
13
açısal konum parametrelerinin tanımlanması ile belirlenebilir. 4 uzvunun
konumu ise, 1 uzvuna göre kayar çift ekseni yönünde öteleme yapacağından,
kayar çift ekseni yönünde tanımlanan s14
konum değişkeni ile belirlenir. Bu konum değişkeni öteleme değişkenidir.
Bu durumda elde edilen devre kapalılık denklemi:
AoA + AB = AoB
olur. Bu denklemde 3 değişken (![]() 12,
12,
![]() 13
ve s14) bulunmakta, bunlardan birinin
tanımlanması ile diğer ikisinin elde edilebilmesi için bir vektör devre
denklemi bulunmaktadır. (tanımlanması gereken bağımsız parametre, uygulamaya
göre,
13
ve s14) bulunmakta, bunlardan birinin
tanımlanması ile diğer ikisinin elde edilebilmesi için bir vektör devre
denklemi bulunmaktadır. (tanımlanması gereken bağımsız parametre, uygulamaya
göre, ![]() 12
(pompa gibi) veya s14 (içten yanmalı
motor) olabilir). Bu örnekte AoA ve AB vektörlerinde
boyut sabit yön değişken iken, AoB vektöründe y bileşeni
sabit (c uzunluğu) ve x bileşeni (s14)
değişkendir. Kompleks sayılar ile bu vektörler yazıldığında vektör devre
denklemi:
12
(pompa gibi) veya s14 (içten yanmalı
motor) olabilir). Bu örnekte AoA ve AB vektörlerinde
boyut sabit yön değişken iken, AoB vektöründe y bileşeni
sabit (c uzunluğu) ve x bileşeni (s14)
değişkendir. Kompleks sayılar ile bu vektörler yazıldığında vektör devre
denklemi:
a2![]() +a3
+a3![]() =
s14 + ic
=
s14 + ic
olur.
Vektör devre denkleminde kullanılan değişkenler, tanımlanan boyutlar
her zaman aynı olmayabilir, problemi tanımlayan kişiye göre farklar gösterebilir.
Örneğin, krank biyel mekanizmasında B mafsalını sökmektense A mafsalı
sökülebilir (alttaki şekil). Bu durumda 3 uzvunun konumunun belirlenmesi
için faklı bir açı ![]() 13'=
13'=
![]() xBA tanımlanması
gerekebilir. Burada dikkat edilecek husus B mafsalının söküldüğünde tanımlanan
xBA tanımlanması
gerekebilir. Burada dikkat edilecek husus B mafsalının söküldüğünde tanımlanan
![]() 13
parametresi ile
13
parametresi ile ![]() 13'
arasında sabit bir açı farkı vardır (bu durumda 180o). Elde
edilen devre kapalılık denklemi ise:
13'
arasında sabit bir açı farkı vardır (bu durumda 180o). Elde
edilen devre kapalılık denklemi ise:
AoA = AoB + AB
dir. Kompleks sayılar kullanılarak yazıldığında:
a2![]() =
s14 + ic +a3
=
s14 + ic +a3![]() '
'
Örnek : altı uzuvlu bir mekanizmadaki devreler

Dört Çubuk mekanizmasına baktığımızda, geometrik olarak:
AoA +AB = AoB
bir vektör denklemi yazılabilir. Ancak Bu denklemde AoB
vektörünü incelediğimizde bu vektörün hem yönü ve hemde boyutu (x ve y
bileşkeleri) değişken olup bu değişkenler hiç bir şekilde bir mafsalla
serbestliği ile ilişkili değildir. Bu denklem sadece diğer iki vektörün
şiddeti ve yönü biliniyor ise, B noktasının konumunu veren AoB
vektörünü bulmaya yarar. Bu denklem geçerli bir vektör denklemi ise de
vektör devre denklemi değildir. Bu tür denklemlerle devre kapalılık denklemleri
arasında en önemli fark, değişken parametrelerin mafsal serbestlik derecesine
bağlı olup olmadığı ve bu denklemlerin bir mafsalın sökülmesi ile yok
olup olmadığıdır.
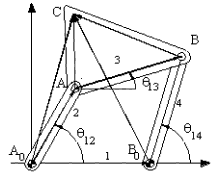
Benzer bir değerlendirme C biyel noktası (3 uzvu) kullanılarak yazılan vektör denklemleri:
|
AoA + AC = AoC
|
ve
|
AB + BC = AC |
içinde yapılabilir.
İkinci denklemde üç vektörde aynı uzuv üzerindedir ve birbirlerine göre sabit açılar oluştururlar. Bu vektörlerden herhangi birinin konumu ve yatay ile yaptığı açı bilinir ise, diğer vektörlerin başlangıç konumu ve yatay ile yaptıkları açı bulunabilir.
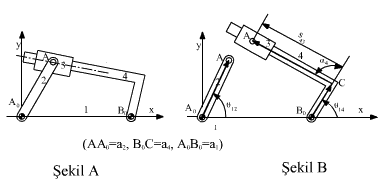
Başka bazı mekanizmaların analizi için iki uzuv üzerinde bulunan iki noktanın anlık çakışma konumu bir vektörün başlangıç veya bitiş noktası olarak kullanılabilir. Kol-kızak mekanizmasında görüldüğü gibi, bu durumda kullanılması gereken parametre bir uzvun diğer uzva göre bağıl konumunu belirleyen değişkendir. BoA vektörü : BoC ve CA olmak üzere iki bileşene ayılabilir, görülen iki açık zincir kullanılarak (ve sonuçta her iki açık zincirden elde edilen A noktasının daima çakışan nokta olması gerektiği göz önüne alınarak) vektör devre denklemi:
AoA = AoBo + BoC + CA
dir. Kompleks sayılar ile yazıldığında:
![]()
A2 ve A3 noktaları daima çakışan noktalardır ve
Şekil B de sökülerek elde edilen iki açık zincir kullanılarak devre kapalılık
denklemi yazılmıştır. A4 noktası ise A2 ve A3
noktaları ile sadece anlık çakışmakta, ![]() t
süre sonra mekanizmada uzuvların yer değişimi ile 3 uzvu 4 uzvuna göre
kayar çift ekseni yönünde
t
süre sonra mekanizmada uzuvların yer değişimi ile 3 uzvu 4 uzvuna göre
kayar çift ekseni yönünde ![]() s
kadar ilerlemesi sonucunda A2 ve A3 noktaları ile
4 uzvu üzerinde farklı bir nokta (A') anlık çakışmış olacaktır (Şekil
C).
s
kadar ilerlemesi sonucunda A2 ve A3 noktaları ile
4 uzvu üzerinde farklı bir nokta (A') anlık çakışmış olacaktır (Şekil
C).
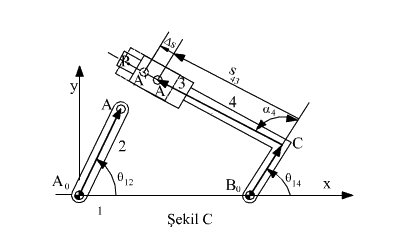
CA vektörünün hem uzunluğu ve hemde açısal konumu değişecektir.
Ancak CA vektörünün BoC vektörüne göre bağıl
açısal konumu, her iki vektör aynı uzuvda bulunan noktalar arasında olduğundan
daima sabittir. Eğer BoC vektörünün sabit x ekseni ile
yaptığı açı ![]() 14
ise, CA vektörünün sabit x ekseni ile yaptığı açı
14
ise, CA vektörünün sabit x ekseni ile yaptığı açı ![]() 14+
14+
![]() 4
olacaktır ve
4
olacaktır ve ![]() 4
açısı 4 uzvu üzerinde bulunan BoC ve CP doğrularının arasında
kalan (P kayar çift ekseni üzerinde her hangi bir noktadır) sabit bir
uzuv parametresidir. Bu durumda devre kapalılık denkleminde konum değişkenleri
4
açısı 4 uzvu üzerinde bulunan BoC ve CP doğrularının arasında
kalan (P kayar çift ekseni üzerinde her hangi bir noktadır) sabit bir
uzuv parametresidir. Bu durumda devre kapalılık denkleminde konum değişkenleri
![]() 12,
12,
![]() 14
ve s43 dür.
14
ve s43 dür.
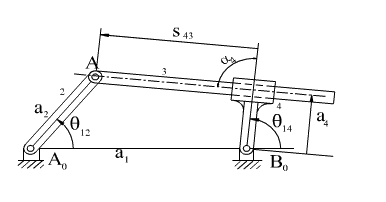
Yukarıda gösterilmiş olan mekanizmayı inceler isek, 2 ve 3 uzuvları üzerinde
daima çakışan A noktasını söküp elde edilen açık zincirleri kullanarak
devre kapalılık denklemlerini yazdığımızda, Bir önceki örnekte (kol-kızak)
gösterilmiş olan mekanizma için elde edilen denklemlerin aynen elde edildiği
görülecektir.Bu nedenle, mekanizma görünümleri farklı olsada kinematik
açıdan aynıdır. Tasarım olarak 3 ve 4 uzuvları farklı şekillerde üretilmiş
iselerde, her iki mekanizmada eğer sabit uzuv parametreleri (a2,
a4, ![]() 4)
aynı ise, aynı harekete sahiptirler.
4)
aynı ise, aynı harekete sahiptirler.

Devre kapalılık denklemleri yazılırken denklemin sadece o konumda geçerli
olmayıp her konum için kullanılacağı unutulmamalıdır. Verilmiş olan mekanizma
özel bir konumda olabilir veya özel boyutlara sahip olabilir. Örneğin
yukarıdaki şekilde mekanizmanın çizildiği konumda 2 ve 1 uzuvları aynı
doğrultuda bulunmaktadır. 2 uzvu kısa bir süre sonra bir miktar dönebilir
ve farklı bir açıda olabilir. Bu durumlarda mekanizmayı bu özel konumdan
biraz kaydırarak çizmemizde yarar vardır . Diğer bazi durumlarda ise devre
kapalılık denklemleri mümkün olabilecek en basit şekilde yazılabilmesi
için mekanizmanın özel boyutları denklemde kullanılarak yazılabilir. Örneğin
kol kızak mekanizmasında gösterilen mekanizma için eğer ![]() 4
açısını önceden bir dik açı olacağı biliniyor ise, bunun devre kapalılık
denklemi kullanılırken kullanılmasında yarar vardır. Bu durumda bu mekanizma
için kompleks sayılarla devre kapalılık denklemi:
4
açısını önceden bir dik açı olacağı biliniyor ise, bunun devre kapalılık
denklemi kullanılırken kullanılmasında yarar vardır. Bu durumda bu mekanizma
için kompleks sayılarla devre kapalılık denklemi:
![]()
Verilen her bağımsız parametre için devre kapalılık denklemlerinden diğer konum değişkenleri için çözüm elde edilmesi mümkün olmayabilir. Bu durumlar mekanizmanın o bağımsız parametre değerinde bağlanamıyacağını veya mekanizmanın o bağımsız parametre değeri konumunda olamıyacağını gösterir.
Düzlemsel mekanizmalar için mekanizmada bulunan devre sayısı (L) kadar vektör devre denklemi yazıldığında, devre sayısının iki katı kadar skaler denklem elde edilmiştir. Denklemlerde kullanılan konum değişkenlerinden F serbestlik derecesine karşı gelen parametreler önceden belirlenmelidir (bunlar bağımsız konum değişkenleridir). Bu denklemlerde bağımsız konum değişkenleri dışında eğer 2L kadar konum değişkeni bulunuyor ise, teorik olarak mekanizmada hareket belirlidir ve devre kapalılık denklemleri kullanılarak diğer konum değişkenleri değerleri o konum için bulunabilir. Bağımsız konum değişkeni verilen sınırlar içinde belirli aralıklarla değiştirilir ve diğer konum değişkenleri değerleri değişik bağımsız değişken değerleri için bulunur ise, incelemiş olduğumuz mekanizmanın tüm çalışma aralığında kinematik analizi yapılmış olur. Eğer bağımsız parametre bir giriş kolu ise (krank) kol açısı 0 ile 360o aralığında değiştirilir . Bağımsız parametre bir hidrolik veya pnömatik pistonun hareketi ise, hareket sınırları pistonun kapalı boyutundan başlayarak pistonun önceden bilinen stroku kadar değişebilir.
Devre kapalılık denklemlerinden konum değişkenleri çözüldükten sonra her hangi bir uzvun üzerinde bulunan her hangi bir noktanın konumu bu konum parametreleri kullanılarak bağımsız değişken değerine göre kolaylıkla bulunabilir.
![]() Devre kapalılık denklemlerinin elde edilmesi için her zaman mekanizmada
mafsalların sökülmüş halde gösterilmesine gerek yoktur. Devamlı çakışan
iki noktayı birbirinden ayırma (sökme) ve sonra birleştirme kavramsal
olarak yapılması gereken bir işlemdir. Başlangıç örneklerinde konunun
görsel olarak anlatılabilmesi için, mafsallar sökülü olarak gösterilmiştir.
Devre kapalılık denklemlerinin elde edilmesi için her zaman mekanizmada
mafsalların sökülmüş halde gösterilmesine gerek yoktur. Devamlı çakışan
iki noktayı birbirinden ayırma (sökme) ve sonra birleştirme kavramsal
olarak yapılması gereken bir işlemdir. Başlangıç örneklerinde konunun
görsel olarak anlatılabilmesi için, mafsallar sökülü olarak gösterilmiştir.
Aşağıda değişik mekanizmalar için yazılmış olan devre kapalılık denklemleri görülmektedir. Sizlerin bu denklemlerin yazılması sırasında hangi mafsalın sökülüp takıldığını belirlemeniz gerekmektedir.
Bilhassa son yıllarda geliştirilmiş olan paket programların kullanılması sırasında en önemli husus bu devre denklemlerinin doğru değişkenler kullanılarak doğru yazılmasıdır. Göreceksiniz ki eğer devre denklemini yanlış yazar isek yapacağımız diğer tüm hesaplar yanlış olacaktır. Bu yöntem ile, somut bir mekanizmanın matematiksel denklemleri yazıldığında soyut matematiksel bir probleme indirgenebilmiştir. Bundan sonra çeşitli yöntemlerle bu denklemleri çözebiliriz.
Örnek I.
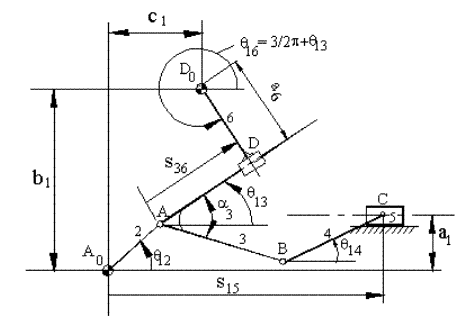
(A0A=a
A0A + AB + BC = A0C ![]()
A0A + AD = A0D0
+ D0D ![]()
Örnek II.
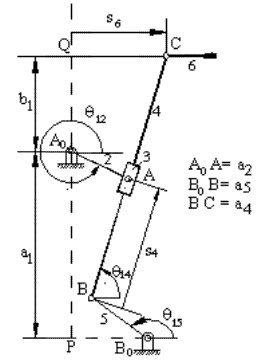
A0A = A0B0
+ B0B + BA ![]()
A0C = A0B0
+ B0B + BC ![]()
Örnek III.
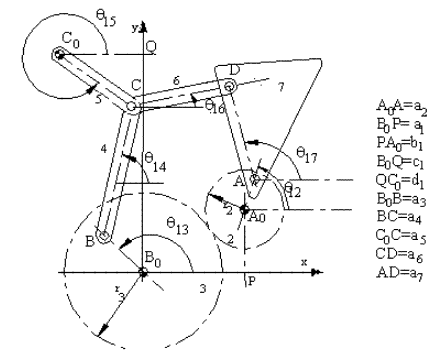
B0B + BC + CD = B0A0
+ A0A + AD ![]()
B0B + BC = B0C0
+ C0C ![]()
Ayrıca dişli çiftten dolayı : r3![]() 13=
-r2(
13=
-r2(![]() 12-
12-![]() 2)
(
2)
(![]() 13=0
iken
13=0
iken ![]() 12=
12=![]() 2)
2)