7.6 Straight Line Motion Mechanisms-1
Two particular coupler-point curve shapes are of particular importance in mechanical design. These are straight-line and circular arcs. Note that the coupler point curve which is a sixth order curve is not in general a straight line or a circular arc. However, in great many design problems, it is sufficient if only a portion of the coupler curve closely approximates the required shape
One of the applications of a circular arc coupler curve is for designing 6-link mechanisms with dwell (If the output of a mechanism remains stationary for a certain period during which the input parameter changes, the mechanism is called a dwell mechanism). As an example, consider the slider-crank mechanism with its coupler point, C, tracing a circular arc for a portion of crank rotation . Let us add two links CD and DD0 such that length CD corresponds to the radius of the approximate circular arc traced by coupler point C and D is the center of this circular arc. Then, as point C traces this circular arc, point D will remain stationary for a crank rotation f0 and there will be no motion of the link DD0 . When point C deviates from this circular arc, link DD0 will start its oscillation (the amount of oscillation y0 is dependant on the length DD0 ).
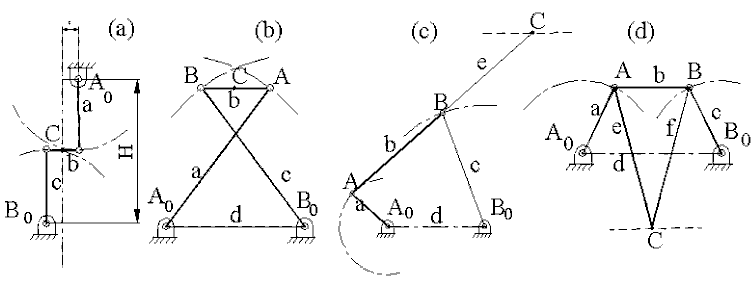
Straight-line motion mechanisms are also important in machine design. Usually a prismatic pair is hard to manufacture (in comparison to revolute joints) and the side forces of the sliders create wear and friction, and in certain applications sliders cannot be used due to space limitations: In fact, in the early application of mechanisms, the straight line motion generation was the greatest problem. There are several straight-line motion mechanisms that have been found during industrial revolution. Of these Watt's (a): a=c=H/2, e= 1/9 H, b= 2/9 H; Chebyshev (b): d=1, a=c=1.25, b=0.5, AC=0.5b; Hoecken (c): a=1, d=2, b=c=e=2.5 and Roberts (d): d=1 b=0.0.538, a=c= 0.530, e=f=1.04 straight-line mechanisms are quite famous (Other dimensions for these mechanisms are also possible. Using different dimensions one can increase the length of the straight line at the cost of the error involved in generating this straight line. Also note that mechanisms b and c, although they have different names in the literature, are cognates of each other).
One can also obtain straight-line motion using slider-crank and swinging-block mechanisms. We shall explain some of these applications in more detail and discuss the related design charts.