3.4 Vector Loops of a Mechanism
The main difference between freely moving bodies and the moving links in a mechanism is that they have a constrained motion due to the joints in between the links. The links connected by joints form closed polygons that we shall call a loop. The motion analysis of mechanisms is based on expressing these loops mathematically.
In kinematic analysis we shall assume that all the necessary dimensions of each link is given and link length dimensions (i.e. the distance between the joints or the angles) can be determined from the given dimensions using the geometry of the link.
In Section 2.1.2, we have seen that it is sufficient to represent the position of each link (rigid body) by describing the position of any two points on that link. One way of selecting these two points on a link is to use the permanently coincident points. It is obvious that in such a procedure, the origin of a vector will be defined by the previous vector and thus the number of parameters to define the link positions will be decreased.
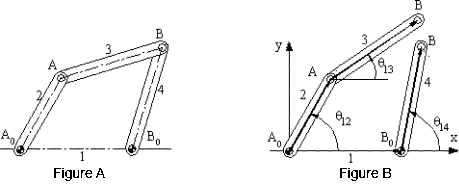
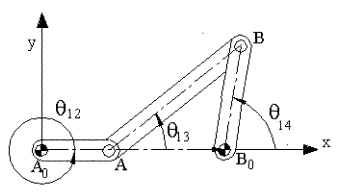
Let us consider a four-bar mechanism as shown above as a simple example.
In this mechanism A0 ,is a permanently coincident
point between links 1 and 2, A is peranently coincident point between
links 2 and 3, B between 3 and 4 and B0 between 1 and 4.
Let us disconnect joint B. In such a case we will obtain two open kinematic
chains A0 AB (links 2,3) with two degrees of freedom and A0 B0B (links 1,4)
with one degree of freedom (Fig.2.7b). To determine the positions of the links
we must have a reference frame. One obvious choice is to select the fixed pivots
A0, B0 as one of the co-ordinate axes and select A0 or B0 as the origin.
Next,in order to define the position of link 2, we must define angle ![]() 12 , which is
related with the degree of freedom of the joint between links 1 and 2. To
determine the position of link 3, since the location of the permanently
coincident point A between 2 and 3 can be determined when
12 , which is
related with the degree of freedom of the joint between links 1 and 2. To
determine the position of link 3, since the location of the permanently
coincident point A between 2 and 3 can be determined when ![]() 12 defined,
we must now define
12 defined,
we must now define ![]() 13 , which is related to the freedom of the joint between
links 2 and 3. Similarly
13 , which is related to the freedom of the joint between
links 2 and 3. Similarly ![]() 14 must be defined to determine the position of link 4.
Hence we need 3 parameters (
14 must be defined to determine the position of link 4.
Hence we need 3 parameters (![]() 12 ,
12 ,
![]() 13 and
13 and ![]() 14 )
which are all related to the joint
freedoms for the open kinematic chains obtained when we disconnect a joint
to eliminate a loop.
14 )
which are all related to the joint
freedoms for the open kinematic chains obtained when we disconnect a joint
to eliminate a loop.
Each link can be defined by a vector fixed on that link, let us select
the permanently coincident points between the links as the tips of these
vectors and define vector A0A (for link 2), AB (for
link 3), B0B (for link 4) and A0B0
(for link 1). Except A0B0 , the other
three vectors will be a function of time (since the distances between
the two points on the same link are fixed, the magnitudes will remain
constant but the directions of these vectors will change in time). Since
the mechanism contains revolute joints only, The magnitude of the vectors
are constant link lengths(A0A=a2, AB=a3,
A0B0=a1 ve B0B=a4).
The angular orientation of these vectors will be rotation variables (![]() 12
,
12
, ![]() 13
ve
13
ve ![]() 14
). When the joint at B is disconnected, B3 and B4 may not be coincident. For the open kinematic chain, the position of point B may be defined
in two different forms as:
14
). When the joint at B is disconnected, B3 and B4 may not be coincident. For the open kinematic chain, the position of point B may be defined
in two different forms as:
A0A +AB=A0B3 (1,2,3 open loop)
A0B0 +B0B= A0B4
(1,4 open loop)
However, at every instant the revolute joint between links 3 and 4 must exist and point B must remain a permanently coincident point for different values of the position variables if the system we are considering is a mechanism. Therefore the vector A0B3 and A0B4 obtained from the two equations using the two open kinematic chains must be equal and this results with the vector equation::
A0A +AB=A0B0 +B0B
This vector equation must be valid for all positions due to the permanetly coincident points.
If this vector equation can nott be satisfied for a given input angle, then that position cannot exist (mechanism cannot be assembled at that position).
In a four-bar mechanism there is a single loop formed and the vector equation describes the closure of this loop mathematically.The
equation(s) that describes the closure of the loop(s) formed in the mechanism
are known as loop closure equation(s). The variables in the loop
closure equations are always related by the joint freedoms and we can
solve for two position variables from any loop equation.
In plane the vector equation will correspond to two scalar equations. In the four-bar example there are three variables (![]() 12,
12,
![]() 13
and
13
and ![]() 14) which we shall call "position variables".
If one of the position variable ( say
14) which we shall call "position variables".
If one of the position variable ( say ![]() 12
), the other position variables (
12
), the other position variables (![]() 13
and
13
and ![]() 14)
can be solved from this vector loop equation. The number of independent parameters that are required will always be equal to the degree-of-freedom of the mechanism.
The relation between the position variables is a nonlinear, trigonometric relation.
14)
can be solved from this vector loop equation. The number of independent parameters that are required will always be equal to the degree-of-freedom of the mechanism.
The relation between the position variables is a nonlinear, trigonometric relation.
One simple and concise form of writing the vector loop equations is to
use complex numbers. for example, If the length of the vector A0A
is a2 and if the vector makes an angle ![]() 12:
12:
A0A = a2cos![]() 12+
ia2sin
12+
ia2sin![]() 12
12
or, using Euler's equation:
A0A = a2![]()
In a similar fashion if the link lengths are denoted as ai
olarak ( a1= A0B0 , a2= A0A,
etc.) the vector loop equation in complex numbers can be written as:
a2![]() +a3
+a3![]() =a1+a4
=a1+a4![]()
If required, the equation can be written in cartesian coordinates as:
a2cos![]() 12
+ a3cosq
12
+ a3cosq![]() 13
= a1 + a4cos
13
= a1 + a4cos![]() 14
14
a2sin![]() 12
+ a3sinq
12
+ a3sinq![]() 13
= a4sin
13
= a4sin![]() 14
14
In case of a four-bar, the vectors in the loop closure equation have
fixed magnitudes. However, the angular inclinations of the three vectors
representing the moving links will change. Hence, there are three position
variables (![]() 12,
12,
![]() 13
and
13
and ![]() 14).
If one of these variables is defined, the remaining two variables can
be solved from the vector equation. If we refer to the definition of the
degree-of-freedom of a mechanism, the variable that must be defined is
the input variable and for a constrained motion the number of input variables
must be equal to the degree-of-freedom of the joints involved. In case
of a four-bar, since all the connections are revolute joints, the variables
are all rotation variables. In case of a prismatic joint, the variable
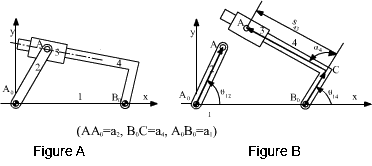
will be the magnitude of a vector or a vector component. Consider a slider-crank
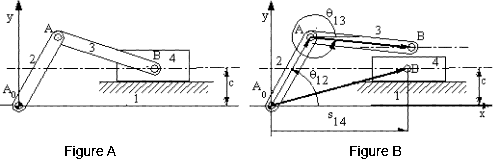
mechanism as shown in Fig. A..
Let us disconnect the revolute joint at B (Fig.B).
In order to determine the positions of links 2 and 3 we must define
14).
If one of these variables is defined, the remaining two variables can
be solved from the vector equation. If we refer to the definition of the
degree-of-freedom of a mechanism, the variable that must be defined is
the input variable and for a constrained motion the number of input variables
must be equal to the degree-of-freedom of the joints involved. In case
of a four-bar, since all the connections are revolute joints, the variables
are all rotation variables. In case of a prismatic joint, the variable
will be the magnitude of a vector or a vector component. Consider a slider-crank
mechanism as shown in Fig. A..
Let us disconnect the revolute joint at B (Fig.B).
In order to determine the positions of links 2 and 3 we must define ![]() 12and
12and
![]() 13.
To locate the position of link 4 its displacement along the slider axis
must be known and the position variable s14
must be defined. The resulting loop closure equation is:
13.
To locate the position of link 4 its displacement along the slider axis
must be known and the position variable s14
must be defined. The resulting loop closure equation is:
AoA + AB = AoB
Again there are 3 variables (![]() 12,
12,
![]() 13
and s14) one of which must be specified
as the input. In this case the vectors AoA and
AB have fixed magnitudes and varying directions. The vector
AoB has a fixed y component (length c) and a changing
x component (s14). Depending on the applications either
13
and s14) one of which must be specified
as the input. In this case the vectors AoA and
AB have fixed magnitudes and varying directions. The vector
AoB has a fixed y component (length c) and a changing
x component (s14). Depending on the applications either
![]() 12
(i.e. in pumps) or s14 (i.e. internal combustion engines)
is the input.In complex numbers the vector loop equation
will be:
12
(i.e. in pumps) or s14 (i.e. internal combustion engines)
is the input.In complex numbers the vector loop equation
will be:
a2![]() +a3
+a3![]() =
s14 + ic
=
s14 + ic
The vectors defined and the variables used in the loop closure equations
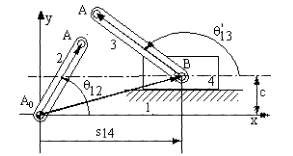
are not unique. For example, for the slider crank mechanism, rather than
disconnecting the revolute joint at B, one can as well disconnect the
revolute joint at A between links 2 and 3 (Fig C).
We must now define the angle ![]() 13'=
13'=
![]() xBA instead
of the angle
xBA instead
of the angle ![]() 13
o determine the position of link 3. Note that the angles.
13
o determine the position of link 3. Note that the angles. ![]() 13
and
13
and ![]() 13'
differ by a constant angle (In this case by 180o). The resulting loop equation is:
13'
differ by a constant angle (In this case by 180o). The resulting loop equation is:
AoA = AoB + AB
or in complex numbers:
a2![]() =
s14 + ic +a3
=
s14 + ic +a3![]() '
'
Example : The loop closure equations of a six link mechanism
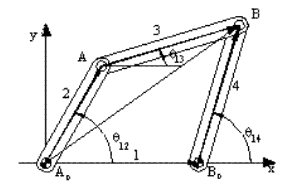
Referring to the four-bar mechanism above, one can write a vector equation in the form::
AoA +AB = AoB
Considering the vector AoB the magnitude and direction
of this vector are variables (or its x and y components) and these variables
are not related with the joint freedoms.we can solve for the vector AoB
provided that the magnitudes and the directions of the other two vectors
are known. Such an equation will not help us for the solution of position
variables. Although it is a valid vector equation, it
is not a loop closure equation. One can identify such loops
by noting the variables involved are not related with the joint freedoms
and these equations are not obtained by disconnecting the joints.
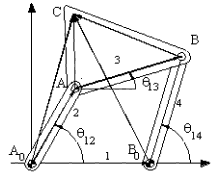
A similar argument can also be made for the vector equations:
|
AoA + AC = AoC
|
ve
|
AB + BC = AC |
In the later case, all three vectors are on the same link and they have a fixed orientation with respect to each other. If the origin and the angular orientation of one of the vectors is known, due to rigidity the orientation of the other vectors will be known.
In certain other cases we may have to use instantaneously coincident points or other points on the links as the tips of the vectors, as shown in Fig. 2.14. The variable involved in such a case is the relative displacement of one link with respect to another link. The vector BoA can be separated into two components: BoC and CA so that one component is of constant magnitude and the magnitude of the other vector is related to the displacement of the prismatic joint between links 3 and 4. The loop closure equation can than be written in the form:
AoA = AoBo + BoC + CA
or in complex numbers:
![]()
Points A2 ve A3 are permanently coincident points. Point A4
is instantaneously coincident with point A3 when the mechanism is moved from this position the two points will be displaced by a distance
![]() s
along the slider axis relative to each other. Points A2 and A3 will be two other different points that will be coincident with
(A') (Fig. C).
s
along the slider axis relative to each other. Points A2 and A3 will be two other different points that will be coincident with
(A') (Fig. C).
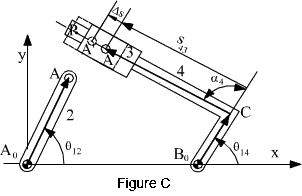
The vector CA changes both its magnitude and direction. However
its orientation with respect to the vector B0C will
be fixed, and no new variable is needed. If the orientation of the vector
B0C is whown by the variable ![]() 14
measured from the positive
x-axis of our reference, the orientation of the vector CA with
respect to positive x
axis is
14
measured from the positive
x-axis of our reference, the orientation of the vector CA with
respect to positive x
axis is ![]() 14+
14+
![]() 4
and angle
4
and angle ![]() 4
is a constant angle measured on link 4 between two lines BoC and CP
(point P is any point on the slider axis on link 4)
The position variables in the loop equation will be
4
is a constant angle measured on link 4 between two lines BoC and CP
(point P is any point on the slider axis on link 4)
The position variables in the loop equation will be ![]() 12,
12,
![]() 14
and s43 .
14
and s43 .
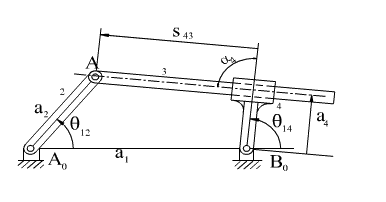
Note that the same vector loop equation can be derived for the swinging block mechanism shown above.
Therefore, the inverted slider crank mechanism is the same as the swinging block mechanism although
their construction is different. Although it is a different construction, If the link dimensions
(a2,
a4, ![]() 4)
are the same, the motion of the two mechanisms will be the same.
4)
are the same, the motion of the two mechanisms will be the same.
When writing the vector loop equations one must be sure that the equations
are valid for every position of the mechanism. The mechanism may be at
a special position such that one or more of the links are collinear as
shown above. (Although
links 2 and 1 are collinear, they will have different orientations at
some other instant). In such a case you may redraw the mechanism slightly
offset from the critical position or show the variable angle ![]() 12
, as shown. In some cases if the constant link angles between two vectors are of a certain simple value (such as 900), then it is advisable to simplifiy the equations accordingly.
For example if the angle
12
, as shown. In some cases if the constant link angles between two vectors are of a certain simple value (such as 900), then it is advisable to simplifiy the equations accordingly.
For example if the angle ![]() 4
of the inverted slider crank mechanism is a right angle, The loop closure equation must be written as:
4
of the inverted slider crank mechanism is a right angle, The loop closure equation must be written as:
![]()
The solution to the loop equations may not exist for every value of the independent parameter. This will mean that for that particular link lengths the mechanism cannot be assembled at the requested position.
-How will you determine the number of independent loops from the number of joints and links?-
In planar mechanisms we can write vector loop equations for each loop of the mechanism. This corresponds to L (L= number of independent loops) vector equations or 2L scalar equations, if we equate the x and y components of vectors. The number of parameters involved in these equations will be 2L+ F, where F is the degree of freedom of the mechanism. If we now define F number of variables (independent variables or input parameters (variables)), then theoretically, we must be able to solve for the other variables (dependent position parameteres). We can change the input variable within a given range in certain increments and obtain the values for the dependent variables. For example if the input variable corresponds to the angle that defines the angular position of an input crank, we change this angle from 0 to 360o. If the input is the movement of a piston inside a cylinder, then we change this length of the piston starting from the closed position to the most extended position (the difference is the stroke of the piston).
When we determine the values of all the position variables corresponding to a certain input variable, then we can determine the position of any point on any link of the mechanism.
![]() One need not draw the mechanism with dismantled joints to write the loop equations. After some practice one can conceptually disconect the joints, identify the loops and the write the necessary loop equations. Initially of course, as a visual aid, we have shown the joints are shown disconnected.
One need not draw the mechanism with dismantled joints to write the loop equations. After some practice one can conceptually disconect the joints, identify the loops and the write the necessary loop equations. Initially of course, as a visual aid, we have shown the joints are shown disconnected.
In the following examples the necessary loop equations for some mechanisms are written. The loop equations and the variables defined are not unique. You are to determine the joint that is disconnected when writing the given loop equation.
In recent years different package programs are available for the analysis of mechanisms. When using these programs, you must input these loops by telling the program which link is connected to which link by what kind of a joint (i.e. what kind of freedom is permitted by that joint). If you are using mathematical packages such as matlab or mathcad, you must type these equations in one form or another. A slight mistake in the loop equations results with erroneous results. Please keep in mind that these equations define the mathematical model of an existing mechanism. This mathematical model can be solved in different ways as we shall see in the coming sections.
Example I.
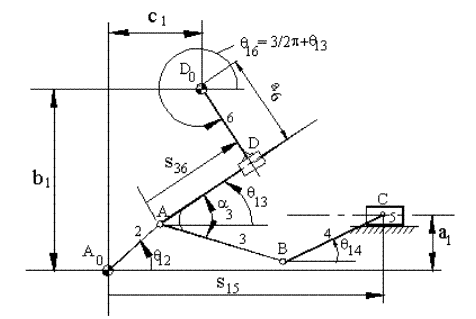
(A0A=a
A0A + AB + BC = A0C ![]()
A0A + AD = A0D0
+ D0D ![]()
Example II.
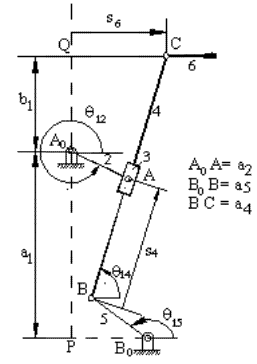
A0A = A0B0
+ B0B + BA ![]()
A0C = A0B0
+ B0B + BC ![]()
Example III.
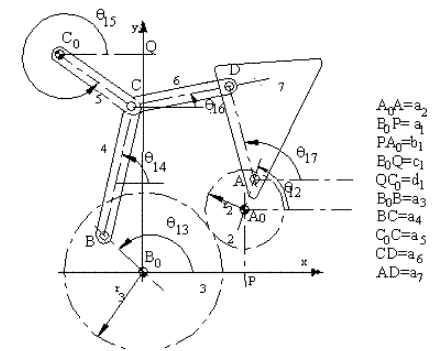
B0B + BC + CD = B0A0
+ A0A + AD ![]()
B0B + BC = B0C0
+ C0C ![]()
Due to the gear pair: r3![]() 13=
-r2(
13=
-r2(![]() 12-
12-![]() 2)
(when
2)
(when ![]() 13=0;
13=0; ![]() 12=
12=![]() 2)
2)