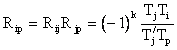5.2. PLANETARY GEAR TRAINS
In simple gear trains the axes of each gear was connected to the fixed link by revolute joints. A gear train is called a planetary gear train if there are some gears whose axes are not fixed. The velocity ratio between the rotating links will be different than the gear ratio. They can produce large changes in speed using very few gears. They are used in differentials, computing devices, in automatic car transmission and in a variety of instruments where a high speed ratio between the input and output is required within a small space (i.e. in heavy duty tractors, hoists, screw drives etc) and/or when a speed change without disengagement of the input and output (i.e. automatic gear boxes) is required.
The simplest form of a planetary gear is as shown. The arm (link k ) can rotate about A0. Link j (which is called sun gear, if external or ring gear, if internal) is also connected to the fixed link by a revolute joint at Ao. Link i, which is called the planet gear, is connected to the arm at A by a revolute joint, and links i and j are gear paired. (In the schematic representation of planetary gear trains side view is usually preferred.)
Planetary Gear Train
Planetary gear trains are also called "Epicyclic Gear Train" from the fact that a point on the planet will describe an algebraic curve which is an epicycloid or hypocycloid. This curve can be represented in parametric form as:
x = a1cosq +a2cosRq
y = a1 sinq +a2sinRq
or in complex numbers:
![]()
Where q is the variable parameter (usually the angle of rotation of the arm) a1, a2 and R are constants (R is a function of the gear ratio, a1 and a2 are the link lengths of the arm and the position of the point relative to the moving pivot of the planet respectively). Very interesting curves (epi- or hypocycloid curves) can be obtained. An example is given in below. One field of application of such motion is in mixers where the pedal or blade is moved on a cycloidal path.
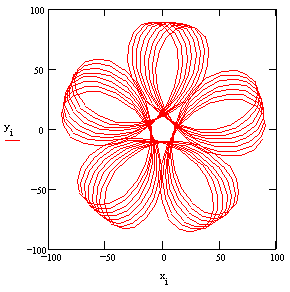
. 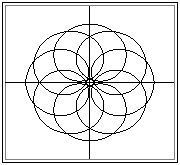
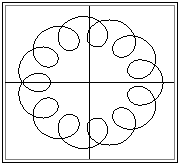
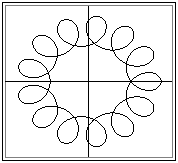
Curves traced by a point on the planet
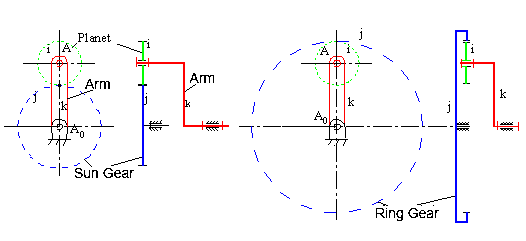
For large force transmission, there is usually more than one planet located symmetrically around the sun gear as shown in Fig. 6.13. Accurate clearance is required for the operation of such a gear train. The planetary gear train thus formed is over closed and thus there must be special dimensional requirements (such that all the planets being equal). In the kinematic analysis of planetary gear trains, one must consider only one planet..
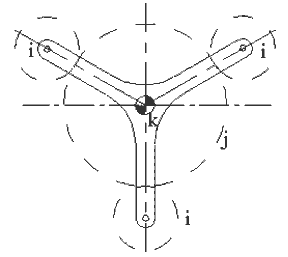
For the motion analysis of planetary gear trains one can refer to the relative motion concept discussed in Chapter 3. The motion of the planet can be considered as composed of two parts. One is the motion of the centre of the planet (point A) and the other is the rotation of the planet about the planet axis. Let us derive an equation that relates the angular speeds of the links and the gear ratio.
Consider the simple planetary gear train as shown in Fig. 6.14. Point P is the point of contact of the gear teeth, and due to pure rolling between the mating gears the velocity of the coincident points Pi and Pj are equal. The velocity of point P can be expressed as:
VPi = VPj = VA + VP/A
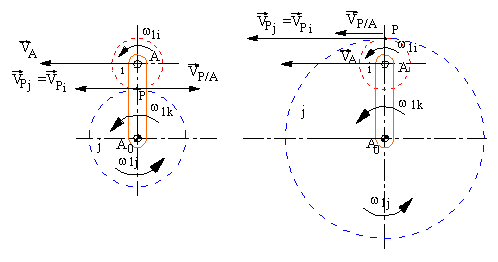
Let us assume that the angular speed is positive if it is counter clockwise. Since the velocities considered are along the same direction (but, may be in opposite sense), the vector velocity equation can be treated as a scalar equation. The velocities can be expressed in terms of angular speeds and the gear radii as:
VPj = VPi = w1j rj
VA = w1k(rj±ri) (+ if external, - if internal mesh)
VP/A=±w1iri (- if external, + if internal mesh)
Where ri and rj are the radii of the gears. Then:
w1j rj=w1k(rj±ri) ± w1iri
or:
| (- if external, + if internal mesh) |
The left side of the equation can be expressed as:
![]()
Note that the definition of the gear ratio is the same for the planetary gear trains and for simple gear trains. For external gearing Rij= -Ti/Tj and for internal gearing Rij =+Ti/Tj. It is also interesting to note that the terms (wlj - w1k) and (w1i - w1k) are really the angular speeds of the sun and planet gears relative to the arm, e.g.:
wkj = (ww1j - ww1k) (angular speed of link j with respect to link k)
wki = (w1i - ww1k) (angular speed of link i with respect to link k)
Therefore:
![]()
or, sometimes it is useful to write this equation in the form:
w1iRij + w1k(1-Rij)-wlj = 0
If the number of teeth on each gear is known, there are three unknowns ( w1j, w1i, and w1k. If any two of the angular speeds are given, one can solve for the third speed.
In simple gear trains the speed ratio, w1j/ w1i, and the gear ratio, Ti/Tj were the same. The symbol Rij was used to represent both of these ratios. In planetary gear trains these two ratios are not the same. Therefore, the symbol Rij will be used as the gear ratio (or the speed ratio when the arm is considered fixed) and the symbol Nij will be used as the speed ratio: Nij = w1j/ w1i. For simple gear trains Rij= Nij.
As a simple example, consider an epicyclic gear train shown below. The sun gear has 60 teeth and the planet has 22 teeth. The arm rotates at 100 rpm counter clockwise and the sun gear rotates at 150 rpm clockwise. Denoting the counter clockwise rotation as positive we obtain:
or: |
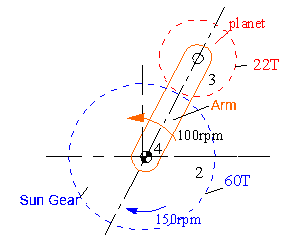 |
As another example, consider the planetary gear train shown below in side view, We can write:
|
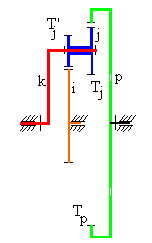 |
Hence the gear ratio has the same meaning as in the simple gear trains.
If there is more than one arm in the planetary gear train, the gear train is called compound planetary gear train. In such a case the above equations must be written for each simple planetary gear train. In Compound gear trains one must first identify gears that have a moving axis of rotation. These gears are the planet gears. Next, one must identify the links that are connected to the planet by a revolute joint. This link is the arm of the planet considered. Then for each arm found, the planetary gear relation must be written. Two examples are given below.
Example
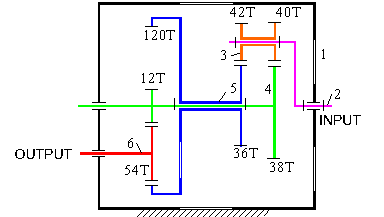
Determine the output speed and the direction of rotation when the input speed is 3000 rpm .
Link 3 does not have a fixed axis of rotation. Therefore it is a planet. Link 2 is connected to link 3 by a revolute joint. Therefore it is the arm. For this planetary system:
![]()
or
![]()
![]()
For the remaining portion of the gear train all the gears have a fixed axis of rotation (they are connected by a revolute joint to link 1) therefore, simple gear train relation yields:
![]() and
and ![]()
or
![]() ;
; ![]()
substituting into the first equation and solving for n16 yields:
![]() and for n12=3000 rpm: n16=-59.8 rpm (in opposite direction of the input speed).
and for n12=3000 rpm: n16=-59.8 rpm (in opposite direction of the input speed).
Note that one can use the angular speed in radians/s or in rpm, since we are involved with the ratio of the speeds.
Example:
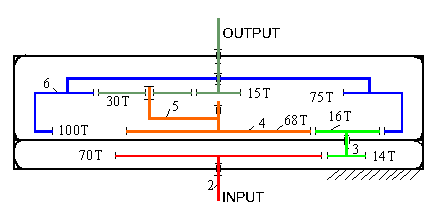
A speed changer is shown. The input speed is 1800 rpm. Determine the output speed and state its relative direction of rotation with respect to the input link.
In the first portion of the gear train (links 2, 3, 4 and 6) the gears have a fixed axis of rotation. Therefore:
![]() or
or ![]()
![]() or
or ![]()
In the upper part of the gear train link 5 does not have a fixed axis of rotation. Therefore link 5 is the planet and link 4 connected to 5 by a revolute joint is the arm. Therefore for this planetary gear train:
![]()
solving for n17 yields:
![]()
(in the same direction with the input link).
In general it is a good practice to carry integer numbers till the end of calculation. Especially in planetary gear trains where very large or very small speed ratios are to be obtained, the difference between two numbers which are close to each other is very critical. Therefore, it is advisable not to use a calculator up to the last step of the computation.