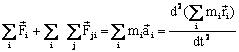6.3. DYNAMIC FORCE ANALYSIS

 

          6.4.1. Center of Mass and Moment of Inertia of a Rigid Body

 

Newton's second law of motion as stated can be applied directly if the body considered is of negligible dimensions. Such bodies we call a particle. Rigid bodies of finite dimensions can be considered to be composed of a system of particles. For the rigid bodies we must define the center of mass and the moment of inertia.

         

 

 

 

 

 

Center of Mass, G, is commonly known as the center of gravity, and is defined as a point on the rigid body whose position is given by :

                    

Where m = Sm_i , total mass of the rigid body. In cartesian coordinates:                                              

            x_G = S x_im_i /m

y_G = S y_im_i /m

Moment of inertia gives us the mass distribution within the rigid body. For rigid bodies in a plane the moment of inertia with respect to an axis normal to the plane and passing through 0 is defined by:                                      

and by definition:

 

Where k₀ is known as the radius of gyration of the rigid body with respect to an axis passing through 0.

The moment of inertia of the rigid body with respect to the center of gravity will be given by:

 

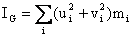
We can write I₀   as:

 

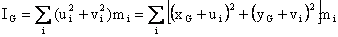
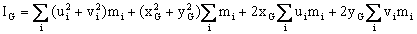
Since u_i and v_i are the coordinates of the particle with respect to the center of  gravity Su_im_i = Sv_im_i = 0. Therefore:

 

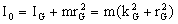
Where k_G is the radius of qyration about the center of gravity and r_G is the magnitude of the position vector of the centar of gravity from 0. We thus have a fundamental theorem:

 

6.4.2. Parallel Axis Theorem:

 

The moment of inertia of a body about any axis is equal to the moment of inertia about a parallel axis passing through the center of gravity plus the product of the mass of the rigid body and the square of the distance between the two axes.

 

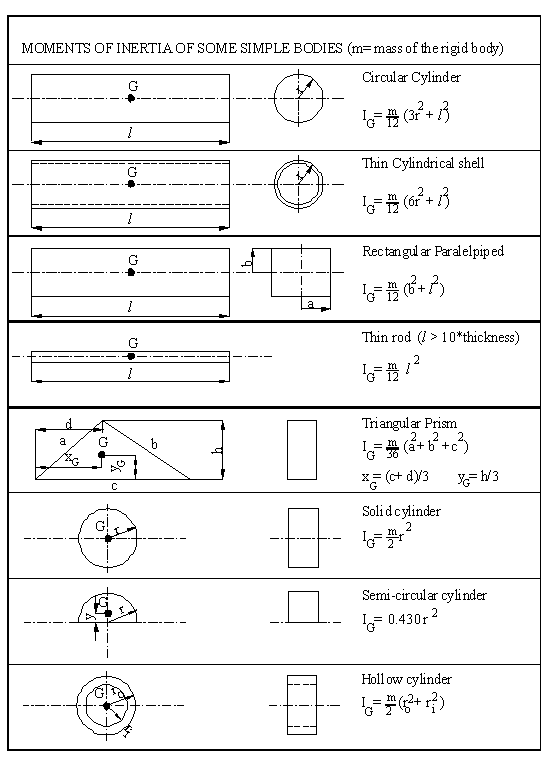
In the following table moments of inertia of some simple bodies are shown: For bodies of a complex shape the moments of inertia can be computed by separating the rigid body into some simple shapes and applying parallel axis theorem. Usually, if a drawing package with a solid modelling is used, the mass and the moments of inertia of the parts can be determined automatically by these packages. In general, the actual manufactured pieces may differ from the drawings in terms of the mass and the moment of inertia. In cases where the moment of inertia of an existing part is required  experimental methods are used to determine these quantities.

 

 

6.4.3. Newton's Second Law of Motion for a Rigid Body

According to Newton's second law the rate of change of momentum of a particle is proportional to the resultant external force acting on the particle. For a particle in the rigid body of constant mass m_i , Newton's second law becomes:

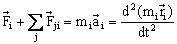                                                    (1)

Where F_i is the external force acting on particle i and F_ji is the force acting on particle i due to particle j. F_ji is commonly known as the internal force. If we consider all the particles within the rigid body:

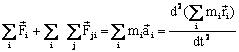                                    (2)

Noting that:

 

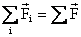= the sum of all the external forces acting on the rigid body.

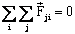   since F_ij + F_ji = 0  due to Newton's third law.

and

.

   

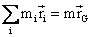  We thus have Newton's Second Law of motion for  Linear momentum for a rigid body, which is:

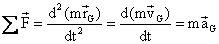                                         (I)

From this equation one can see that the internal force has no effect on the motion of the rigid body, the center of gravity behaves as if the whole mass were concentrated and the resultant force SF were acting upon this point. The term mv_G is known as the linear momentum of the rigid body.

 

Now if we take the moment of the forces in equation (1) with respect to point 0, we obtain:

 

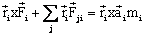                                                                        (3)

The acceleration of point i, a_i, can be written in terms of the acceleration of point 0 and relative accelerations as:

a_i = a₀ + a_i/0 = a₀ + a_i/0 ⁿ+ a_i/0^t

Where a_i/0^t and a_i/0 ⁿ are the relative tangential and normal accelerations of point i with respect to point 0. In vector notation these terms are given by:

 

a_i/0 ^t=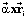

 

a_i/0 ⁿ= -w²r_i

 

Where a and w are the angular acceleration and velocity of the rigid body respectively.

Substituting the above relations into equation (3) and summing up for all the particles within the rigid body results in:

               (4)

Noting that:

                 -

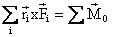= sum of the moment acting along an axis passing through O (perpendicular to the plane).

 

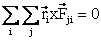 (since F_ij = -F_ji   and these forces have same line of action. The summation will be composed of terms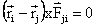  

 The terms on the right hand side of equation (4) can be written as:

 

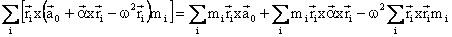  (5)

Now :

 

 

 

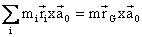
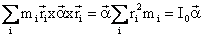
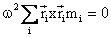
Hence, equation (4) simplifies into:

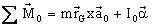                                                          (6)                              

In general 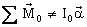. The first term on the right-hand side of equation (v) will vanish if  a₀=0 or r_G=0 or if a₀ and r_G are  parallel. The acceleration of point 0 is zero if point 0 is the acceleration pole or if the rigid body is in a rotation about point 0.

r_G = 0 means that point 0 coincides with the center of gravity G  and a₀ will be parallel to r_G  only in very special cases. However in any general case the center of gravity can be made coincident with the center of the reference axis. We thus have Newton's Second Law of Motion for Angular Momentum of a rigid body, which is:

 

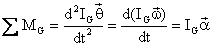                                            (II)

 

Note that both the moment of external forces and the moment of inertia of the rigid body must be with respect to an axis passing through the center of gravity and perpendicular to the plane of motion. The term I_Gw is known as the angular momentum of the rigid body with respect to center of gravity.

 

6.4.4. D'Alambert's Principle

 

Equations I and II can be written in the following form:

 

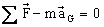                                                                       (I)

and

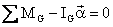                                                                     (II)

 

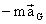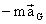     Now the term  has the magnitude of a force. Equation I is a vector equation which states that the vector sum of all the external forces plus the fictitious (nonexistant) force of magnitude and direction   are zero. The fictitious force 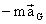 is known as the inertia force which will be denoted by Fⁱ:

 

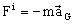
Fⁱ has the same line of action of a_G but is in opposite direction.

 

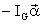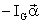Similarly, the term  has the magnitude of a moment and equation II is a vector equation which states that the vector sum of all the external moments about the center of gravity plus a fictitious moment of magnitude and direction  are zero. This fictitious moment is known as the inertia torque and it will be denoted by Tⁱ :

 

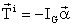
Tⁱ  is in opposite sense of the angular acceleration a. Using inertia force and inertia torque Newton's Second Law of Motion for a rigid body results with the equations:

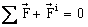
and

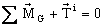
We can as well treat the inertia terms as if they were another external force or moment acting on the rigid body, in which case:

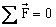
and

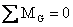
Where the summation includes both the external and inertia forces and moments. This concept is known as D'Alambert's principle which can be stated as follows:

 

 

 

 

D'Alambert's Principle

 

     In a body moving with a known angular acceleration and a linear acceleration of the center of gravity, the vector sum of all the external forces and inertia forces and the vector sum of all the external moments and inertia torque are both separately equal to zero.

 

D'Alambert's principle is very useful in the dynamic force analysis of machinery. In great many problems we know the acceleration characteristics of the members in the machine structure and we can determine the inertia forces and torques. These inertia forces and torques can be treated as if they are external forces and the procedure of static force analysis can be carried out for this dynamic case. However one must never think the inertia forces and moments as real forces. They are fictitious forces and they never exist. Acceleration is a result of the external forces.

 

     In graphical solutions it is convenient to replace the inertia force and torque by an equivalent resultant inertia force.

 

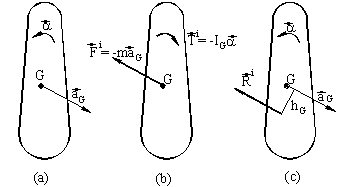
     Consider a rigid body with  a_G as the acceleration of its center of gravity and a as its angular acceleration (Figure.a). The inertia force and torque will be as shown in Figure b. The inertia force and torque can be combined into a single resultant, Rⁱ (Figure c) , if:

 

 

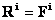
and

 

 

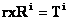
where r is a position vector from the center of gravity to a point on the line of action of Rⁱ. In such a case the resultant Rⁱ has the magnitude and direction of the inertia force Fⁱ and is displaced from the center of gravity by a perpendicular distance h_G such that:

 

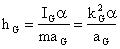
This fictitious force Rⁱ will then replace the effect of the inertia force and torque
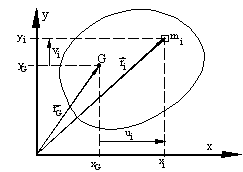
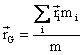