3.6 Devre Kapalılık Denklemlerinin Konum Değişkenleri İçin Çözümü
Önceki kısımda gördüğümüz gibi, geometrik olarak devre kapalılık denklem-lerinin çözümü yeterli parametresi verilmiş olan bir üçgenin diğer parametrelerinin be-lirlenmesinden ibarettir. Analitik geometri derslerinden bildiğimiz gibi, üçgen bağ-lantıları aynı zamanda analitik olarak ifade edilerek analitik çözümde yapılabilir. Bu yaklaşımda, tıpkı geometrik yöntemde olduğu, gibi etap etap konum parametrelerinin belirlenmesine çalışılacak ve bunun için seri olarak çözülebilecek bir dizi denklem elde edilecektir. Her bir konum parametrisinin sadece bağımsız parametreye göre belirlen-mesine çalışılmayacaktır. Yani, bu çalışma sonrası konum parametrelerini bağımsız parametre değerine göre bulabileceği bir "algoritma" elde edilecektir. Bu algoritmayı ister bir hesap makinası ile ister özel bir program yazarak veya ister isek çeşitli paket programlarda kolaylıkla çözmemiz mümkün olacaktır.

İlk örnek olarak yukarıda görülen bir krank-biyel mekanizmasını ele alalım.
Bi-linen uzuv boyutlarını a1, a2, a3
olarak gösterelim. Amacımız 3 ve 4 uzuvlarının her hangi bir krank açısı,
![]() 12,
değeri için bulmaktır.
12,
değeri için bulmaktır.
Vektör devre denklemi:
A0A = A0B + BA
Bu vektörler tanımlanmış olan sabit ve değişken parametrelerle yazıldığında:
|
A0A = a2(cos A0B = xi + a1j BA = a3(cos |
olacaktır.
x ve y bileşenleri ayrı ayrı birbirlerine eşitlendiğinde, devre kapalılık denklemi iki skaler denkleme dönüşecektir:
| a2cos |
(1) |
| a2sin |
(2) |
Bu denklemleri bilinmeyen konum parametreleri için yeniden yazdığımızda:
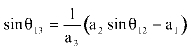 |
(3) |
| (4) |
Verilen giriş kol açısı ![]() 12
değerine göre,
12
değerine göre, ![]() 13
değişken değeri (3) denkleminden, s14
ise (4) denkleminden çözülebilecektir. s14
değişken değeri
13
değişken değeri (3) denkleminden, s14
ise (4) denkleminden çözülebilecektir. s14
değişken değeri ![]() 13
değeri (3) denkleminden bulunduktan sonra bulunabilir. Her hangi bir C
noktasının koordinatlarını, C (xc, yc),
bulmak istediğimizde A0C = xci+ycj
konum vektörü A0C = A0B
+ BC olarak yazılıp x ve y bileşenleri ayrı ayrı eşitlendiğinde:
13
değeri (3) denkleminden bulunduktan sonra bulunabilir. Her hangi bir C
noktasının koordinatlarını, C (xc, yc),
bulmak istediğimizde A0C = xci+ycj
konum vektörü A0C = A0B
+ BC olarak yazılıp x ve y bileşenleri ayrı ayrı eşitlendiğinde:
| xc = s14
+ b3cos( |
(5) |
| yc = a1
+ b3sin( |
(6) |
(5) ve (6) numaralı denklemler (3) ve (4) numaralı denklemler çözüldükten
sonra ele alınabilir.
Şu ana kadar göz önüne alınmamış olan çok önemli bir konu bulunmaktadır.
Bu, (3) denkleminde ![]() 13
konum değişkeninin verilen her hangi bir
13
konum değişkeninin verilen her hangi bir ![]() 12
açısı için çözümü sırasında denklemi sağlayan iki farklı değerde olabileceğidir.
Bunun nedeni kullanılacak olan invers sinus fonksiyonu çift değerlidir.
Yani sinus açısı karşı kenarın hipotenüse oranı olduğundan, verilen bir
sin(
12
açısı için çözümü sırasında denklemi sağlayan iki farklı değerde olabileceğidir.
Bunun nedeni kullanılacak olan invers sinus fonksiyonu çift değerlidir.
Yani sinus açısı karşı kenarın hipotenüse oranı olduğundan, verilen bir
sin(![]() ) değerini
) değerini
![]() açısı sağladığı
gibi (1800-
açısı sağladığı
gibi (1800-![]() )
açısıda sağlayacaktır. Bu açılardan hangisinin mevcut mekanizma için geçerli
olduğu, kullanıcı tarafından belirlenmesi gerekir, çünkü Yukarıda gösterilmiş
olan mekanizma uzuv boyutları aynı olmak üzere, aynı
)
açısıda sağlayacaktır. Bu açılardan hangisinin mevcut mekanizma için geçerli
olduğu, kullanıcı tarafından belirlenmesi gerekir, çünkü Yukarıda gösterilmiş
olan mekanizma uzuv boyutları aynı olmak üzere, aynı ![]() 12
krank açısında istenilir ise, aşağıda gösterildiği gibi farklı bir şekilde
de monte edilebilir. Matematiğin mekanizmayı nasıl monte ettiğimizi bilmesine
imkan yoktur.
12
krank açısında istenilir ise, aşağıda gösterildiği gibi farklı bir şekilde
de monte edilebilir. Matematiğin mekanizmayı nasıl monte ettiğimizi bilmesine
imkan yoktur.
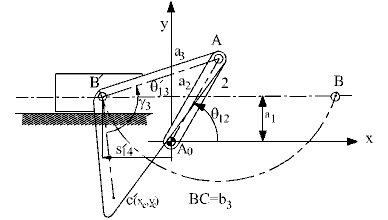
Krank biyel mekanizmasının aynı krank açısında farklı monte edilişi
Devre kapalılık denklemi kullanarak elde ettiğimiz konum parametreleri ara-sındaki ilişki lineer değildir. Bu nedenle her mekanizma için geçerli bir yöntem söylemek mümkün değildir. Yaklaşım genelde üçgenlerin belirlenerek bu üçgenlerin gerekli parametrelere göre çözümünü bulmaktır.
DÖRT ÇUBUK MEKANİZMASI
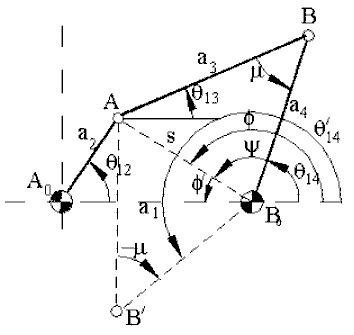
Dört-çubuk mekanizması için kullanılan yönteme "Raven metodu" da denmektedir.
Aşağıda gösterilmiş olan mekanizma için uzuv boyutları (a1,
a2, a3,
a4) verilmiştir. Tüm uzuvların konumunu
her hangi bir ![]() 12
değeri için bulmak istiyoruz.
12
değeri için bulmak istiyoruz.
Geometrik yöntemde kullandığımız yönteme benzer bir şekilde ilk olarak
A0AB0
üçgenini göz önüne alalım. Bu üçgende iki kenar (a1,
a2) ve aralarındaki açı (![]() 12)
bilinmektedir. Öyle ise üçüncü kenar (AB0
= s) ve
12)
bilinmektedir. Öyle ise üçüncü kenar (AB0
= s) ve ![]() '
açısı bu üçgende kosinüs teoremi kullanılarak bulunabilir:
'
açısı bu üçgende kosinüs teoremi kullanılarak bulunabilir:
| (1) | |

|
(2) |
s ve ![]() '
değerlerini belirlemek için bir başka yöntem ise (ki bu yöntemde invers
kosinus fonksiyonu kullanıldığında ortaya çıkacak olan çifte değerlilik
olmayacaktır) B0A vektörünü B0A=B0A0+A0B
olarak yazdıktan sonra :
'
değerlerini belirlemek için bir başka yöntem ise (ki bu yöntemde invers
kosinus fonksiyonu kullanıldığında ortaya çıkacak olan çifte değerlilik
olmayacaktır) B0A vektörünü B0A=B0A0+A0B
olarak yazdıktan sonra :
| scos |
(1') |
| ssin |
(2') |
Her iki denklemin sağ tarafı bir ![]() 12
açısı değerine göre B0A vektörünün
yatay ve dikey bileşenlerini verecektir. Vektörü kutupsal koordinatlarda
gösteren s ve
12
açısı değerine göre B0A vektörünün
yatay ve dikey bileşenlerini verecektir. Vektörü kutupsal koordinatlarda
gösteren s ve ![]() değerlerini bulmak ise dik koordinat sisteminden kutupsal koordinat sistemine
dönüşümdür. Hesap makinalarında bu işlem (R-P) ile gösterilen tuş ile
(dik koordinat sisteminden polar koordinat sistemine dönüşüm) yapılır
ise s ve
değerlerini bulmak ise dik koordinat sisteminden kutupsal koordinat sistemine
dönüşümdür. Hesap makinalarında bu işlem (R-P) ile gösterilen tuş ile
(dik koordinat sisteminden polar koordinat sistemine dönüşüm) yapılır
ise s ve ![]() değerleri elde edilir. Eğer Excel paket programı kullanılır ise
değerleri elde edilir. Eğer Excel paket programı kullanılır ise ![]() açısının bulunması için ATAN2(X,Y) fonksiyonu kullanılabilir. (s için
her iki terimin karelerinin toplamının kare kökü alınır). Mekanizma için
s ve geçerli
açısının bulunması için ATAN2(X,Y) fonksiyonu kullanılabilir. (s için
her iki terimin karelerinin toplamının kare kökü alınır). Mekanizma için
s ve geçerli ![]() değeri bulunduktan sonra, ABB0 üçgeninin
her üç kenar uzunluğu bilindiğinden (s=AB0
(
değeri bulunduktan sonra, ABB0 üçgeninin
her üç kenar uzunluğu bilindiğinden (s=AB0
(![]() 12
nin fonksiyonu olarak), AB=a3, BB0=a4),
kosinus teoremi ile bu üçgenin açı değerleri bulunabilir:
12
nin fonksiyonu olarak), AB=a3, BB0=a4),
kosinus teoremi ile bu üçgenin açı değerleri bulunabilir:
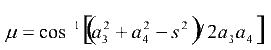
|
(3) |

|
(4) |
![]() ve
ve
![]() açıları
invers kosinüs fonksiyonu ile elde edildiklerinden 0 ile 180o
arasında değer alırlar. Bilinmeyen
açıları
invers kosinüs fonksiyonu ile elde edildiklerinden 0 ile 180o
arasında değer alırlar. Bilinmeyen ![]() 13
ve
13
ve ![]() 14
konum parametreleri eğer mekanizma A0ABB0
şeklinde (açık durum) monte edilmiş ise:
14
konum parametreleri eğer mekanizma A0ABB0
şeklinde (açık durum) monte edilmiş ise:
| (5) | |
| |
(6) |
Eğer mekanizma A0AB'B0 şeklinde (çapraz durum) monte edilmiş ise:
| (5') | |
| |
(6') |
olacaktır. Kol-sarkaç boyutlarında mekanizmalar için her ![]() 12
açısına karşı iki değişik
12
açısına karşı iki değişik ![]() 13
ve
13
ve ![]() 14
değeri elde edilecektir. Ancak, eğer denklem 3 ve 4 de 1 den büyük bir
değerin invers kosinus fonksiyonunun değeri bulunmak istenir ise, çözüm
elde edilemez. Bu, mekanizmanın verilmiş olan
14
değeri elde edilecektir. Ancak, eğer denklem 3 ve 4 de 1 den büyük bir
değerin invers kosinus fonksiyonunun değeri bulunmak istenir ise, çözüm
elde edilemez. Bu, mekanizmanın verilmiş olan ![]() 12
açısında kapalı bir devre oluşturamıyacağını gösterir.
12
açısında kapalı bir devre oluşturamıyacağını gösterir.
Bu şekilde, konum değişkenleri değerlerini hesaplayabileceğimiz bir denklem dizisi elde etmiş bulunuyoruz.
KOL-KIZAK MEKANİZMASI
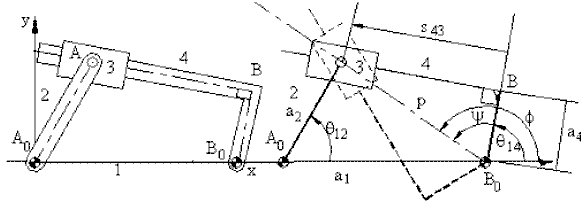
Yukarıda kol-kızak mekanizması gösterilmektedir. Konum analizi için (konum değişkenlerini bulmak için) gereken denklemler:
| pcos |
(1) |
| psin |
(2) |
p ve ![]() nin çözümü için hesap makinalarında P
nin çözümü için hesap makinalarında P![]() R
tuşu veya Excell paket programında
R
tuşu veya Excell paket programında ![]() için ATAN2(X,Y) fonksiyonu kullanılır ise her durumda doğru sonuç elde
edilebilecektir.
için ATAN2(X,Y) fonksiyonu kullanılır ise her durumda doğru sonuç elde
edilebilecektir.
|
(3) |
|
(4) |
|
| (5) |
Bu denklemlerin çıkarılması okuyucuya bırakılmıştır (sıra ile A0AB ve AB0B üçgenlerinin çözümünü düşünmek gerekir).
ÇOK UZUVLU MEKANİZMALAR
Genellikle çok uzuvlu mekanizmalar dikkatlice incelenir ise, büyük bir kısmının dört uzuvlu devrelerden oluştuğu görülecektir. Her bir devre yukarıda üç temel mekanizma için vermiş olduğumuz yöntem ile çözülebilir. Bu durumda giriş uzvunu içeren devreden başlayarak devreler sırayla çözülebilecektir.

Yukarıda gösterilmiş olan var-gel mekanizmasını ele alalım. 1,2,3 ve
4 uzuvlarından oluşan A0AB0
devresi önceden gösterilmiş olan kol-kızak mekanizmanın a4=0
durumundan başka bir şey değildir. Bu devrenin çözümünden ![]() 14
açısı ve s43 elde edilebilecektir. 1,4,5
ve 6 uzuvlarının oluşturduğu B0BCPB0
devresi ise, bir krank-biyel mekanizmasıdır. Bu devrenin herhangi bir
14
açısı ve s43 elde edilebilecektir. 1,4,5
ve 6 uzuvlarının oluşturduğu B0BCPB0
devresi ise, bir krank-biyel mekanizmasıdır. Bu devrenin herhangi bir
![]() 14
açısına göre çözümü ise s16 ve
14
açısına göre çözümü ise s16 ve ![]() 15
konum parametrelerini verir. Seçilen referans eksenlerine göre konum parametrelerinin
tanımına dikkat edilmesi gerekir.
15
konum parametrelerini verir. Seçilen referans eksenlerine göre konum parametrelerinin
tanımına dikkat edilmesi gerekir.
Öyle ise, bilinen ![]() 12
açısına göre diğer konum değişkenleri:
12
açısına göre diğer konum değişkenleri:
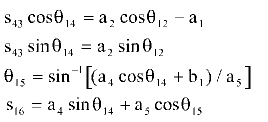
denklemleri kullanılarak elde edilebilir.
İlk iki denklem kol kızak mekanizması için A0AB0
üçgeninin çözümünü, son iki denklem ise krank biyel mekanizmasının (B0BC)çözümünü
vermektedir. ![]() 12
ve
12
ve ![]() 14
açılarının istendiğinde dikey bir doğruya göre ölçülmeyip kolaylıkla yatay
bir doğruya göre ölçülebileceği açıktır. Ayrıca
14
açılarının istendiğinde dikey bir doğruya göre ölçülmeyip kolaylıkla yatay
bir doğruya göre ölçülebileceği açıktır. Ayrıca ![]() 15
değeri belirlenirken invers sinüs kullanıldığından şekil ile uyumlu olabilmesi
için
15
değeri belirlenirken invers sinüs kullanıldığından şekil ile uyumlu olabilmesi
için ![]() 15
açı değeri 900 den küçük olmalıdır.
15
açı değeri 900 den küçük olmalıdır.
Bu kısımda açıklanmış olan yöntem pratikte birçok mekanizmanın analizinde kullanılan çok basit bir yöntemdir. Mühim olan mekanizmayı oluşturan basit devreleri belirlemek ve bu basit devrelerin herbirini ayrı ayrı çözebilmektir.
Örnek
Yukarıda gösterilmiş olan garaj kapısının analizi için gerekli olan denklemleri elde edelim (Bu mekanizmanin hareketi, ilk bölümde gösterilmişti)
Yukarıda verilmiş olan şeklin AutoCad kütüğü için -garajkap.dwg-
Dikkat edilir ise, bir teknik resim üzerinde bizim istediğimiz gibi ne uzuvlar numaralıdır ve nede mafsallar işaretlidir. Bunu bizim yapmamız gerekir. Öncelikle de mekanizmanın serbestlik derecesini bulalım. Mekanizma 6 uzuvlu ve 7 döner mafsala sahip olduğuna göre serbestlik derecesi F=3(6-7-1)+7=1 dir ve bağımsız devre sayısı L=7-6+1=2 dir. Bundan sonra uzuvları ve mafsalları işaretleyelim ve devreleri belirleyelim.
Devreleri belirlerken gerekli olan uzuv boyutlarını verilen teknik resimden bulabiliriz.
Bunlar:
A0B0=a1, A0A=a2, A0D=b2, AB=a3, B0B=a4, BC=a5, DC=a6
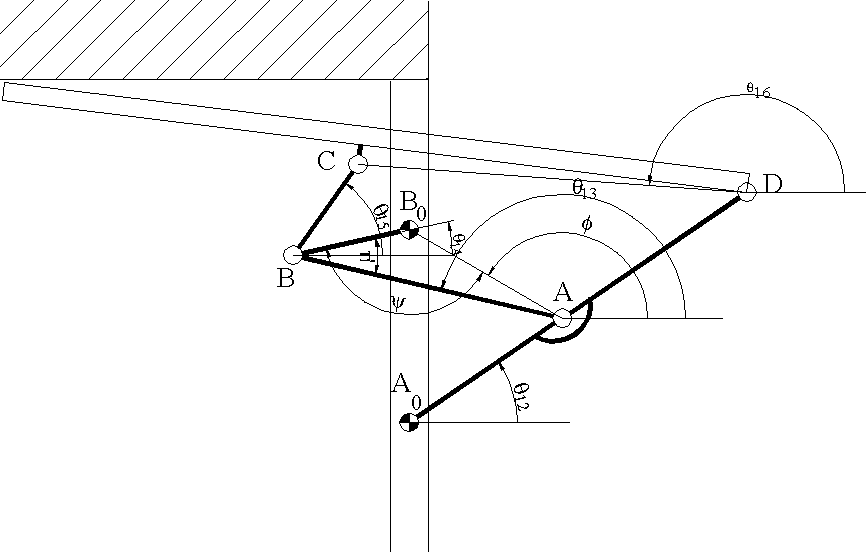
A0ABB0
devresi bir dört-çubuk mekanizmasıdır. Bu devrede ![]() 12
kol açısı bağımsız değişken olduğunu kabul eder isek dört çubuk mekanizmasında
olduğu gibi şu denklemleri yazabiliriz: (B0A=s)
12
kol açısı bağımsız değişken olduğunu kabul eder isek dört çubuk mekanizmasında
olduğu gibi şu denklemleri yazabiliriz: (B0A=s)
scos(![]() )=
- a2cos(
)=
- a2cos(![]() 12)
12)
ssin(![]() )=
a1- a2sin(
)=
a1- a2sin(![]() 12)
12)
Bu iki denklemden s ve ![]() çözüldükten sonra kosinüs teoremi kullanılarak:
çözüldükten sonra kosinüs teoremi kullanılarak:
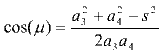
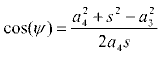
![]() 14=
14=![]() -
-![]()
![]() 13=
13=![]() -
- ![]() +
+ ![]() 14
14
Dört- Çubuk mekanizmasını çözdükten sonra, BCD üçgenini ele alalım. B ve D noktaları koordinatları:
xB=a2cos(![]() 12)+a3cos(
12)+a3cos(![]() 13)
13)
yB=a2sin(![]() 12)+a3sin(
12)+a3sin(![]() 13)
13)
xD=b2cos(![]() 12)
12)
xD=b2sin(![]() 12)
12)
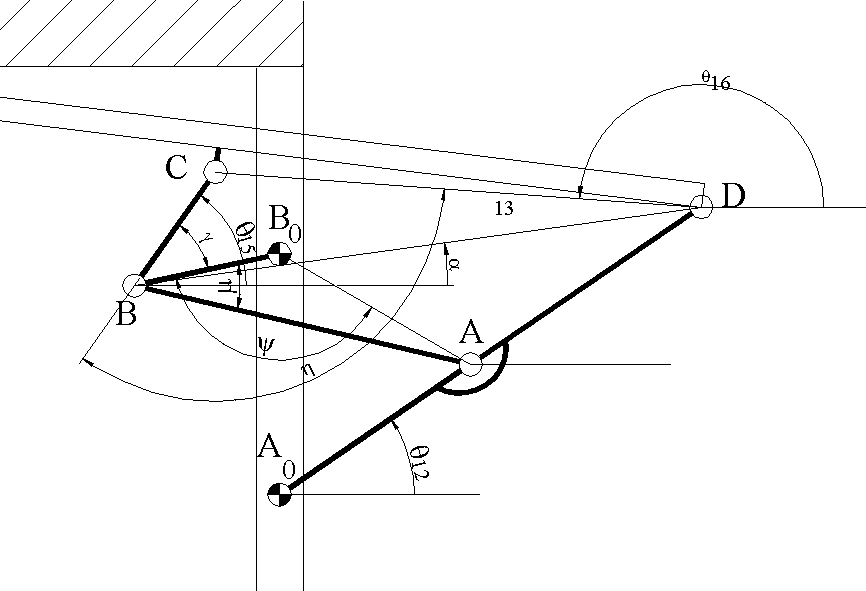
![]()
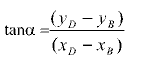
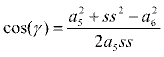
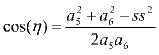
ve
![]() 15=
15=![]() +
+![]()
![]() 16=
16=![]() 15+
15+![]()
Bu şekilde mekanizmanın tüm uzuvlarının konumları bulunmuş olur.