4.1 Hız ve İvme Analizi -1

Düzlemde üç değişik tipte hareketi ayırabiliriz:

Öteleme:

Bir cisim öteleme yapıyor ise, cismin üzerinde her nokta birbirlerine paralel yörüngeler çizecektir ve cisim üzerinde bulunan bir doğru, daima ilk konumuna paralel olacak şekilde hareket edecektir.Bu durumda A, B gibi her hangi iki nokta göz önüne alındığında, birinci konumdan ikinci konuma belirli bir yer değişim olduğunda,

dir ve B noktasının konum vektörü r_B:

     r_B = r_A + r_AB

olarak yazılabilir. Bu noktanın zamana göre türevi, noktanın hızını verecektir:

r_AB vektörünün şiddeti ve açısal yönü değişmediğinden ikinci terim sıfıra eşit olacak ve:

      veya V_A = V_B

olacaktır. Aynı değerlendirmeyi ikinci türev için yapabiliriz ve :

      veya a_A = a_B

olacağını görürüz. Öyle ise: Öteleme yapan cisimlerde cisim üzerinde bulunan her noktanın yer değişim, hızı ve ivmesi birbirlerine eşittir.

Sabit bir eksen etrafında dönme:

Düzlemsel bir hareket için sabit eksen düzleme dik ve düzlemi A₀ noktasında kesen bir eksendir (bu noktaya düzlemsel hareket için dönme merkezi diyeceğiz). Bu durumda rijit cisim üzerinde bulunan her nokta aynı merkezli daire yayları üzerinde hareket edecektir. Şekilde cisim belirli bir yer değişim yapmış olarak iki ayrı konumda görülmektedir ve:

     AA₀A' =BB₀B' =

olacaktır.

Her nokta A₀ merkezli bir daire yayı üzerinde hareket edeceğinden o noktanın yer değişim miktarı, o noktanın A₀ merkezinden uzaklığı ile (radyan olarak ölçülen) açısal yer değişim miktarı çarpımına eşittir. Yani:

      r_A =r_A       r_B =r_B

bu yer değişimin belirli bir zaman aralığında düşünülür ise,

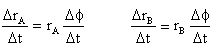
ve t limitte sıfıra gittiği düşünülerek:

Burada v_A and v_B, A ve B noktalarının hız vektörlerinin şiddetidir ve 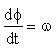cismin açısal hızıdır. Hız vektörlerinin yönü mutlaka o noktayı merkeze bağlayan doğruya dik olacaktır. Vektörel olarak hız vektörü, ve r_A vektör olarak yazılıp vektörel çarpım yapılarak:

      v_A = x r_A

Bu denklemde (x) vektörel çarpım operatörüdür.

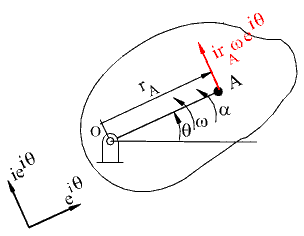
Düzlemsel hareket için hız ve ivmenin gösteriminde kompleks sayılardan da kolaylıkla faydalanılabilir. Örneğin, A noktasının konum vektörü kompleks sayılarla:

      r_A = r_A

olacaktır. Eğer cisim sadece A₀ noktasından geçen düzleme dik bir eksen etrafında dönme yapıyor ise, bu denklemde değişken bir açıdır ve r_A, A noktasının merkezden uzaklığını gösteren parametre bir sabittir. terimi ise A₀A yönünde bir birim vektördür. Konum vektörünün türevi bize o noktanın hızını verecektir:

      v_A= i r_A

Bu denklemde dir. açısal hızı eğer açısının zamana göre değişimi saat yelkovanına ters yönde artıyor ise (veya saat yelkovanı yönünde azalıyor ise), pozitifdir. Saat yönünde zamana göre artış ise negatif bir açısal hızdır. Hız vektörünün şiddeti r_A olup yönü ise i dır. olduğuna göre, dır . Yani, bu yeni birim vektör A₀A doğrusuna göre 90⁰ saat yelkovanına ters yönde dönmüş bir birim vektördür. Hız vektörünün şiddeti daima pozitif alınması durumunda eğer negatif ise, A noktasının hız vektörünün yönü -i, yani olacaktır. Bu durumda hız vektörü A₀A ya yine dik olup A₀A doğrusuna göre saat yelkovanı yönünde dönmüştür. Öyle ise, A noktasının hızının şiddeti r_A olup A₀A ya diktir. Yönü A₀A yönünde bir birim vektörün açısal hızın yönüne göre saat yelkovanı yönünde veya ters yönünde 90⁰ döndürülmesi ile elde edilen bir birim vektör yönündedir.

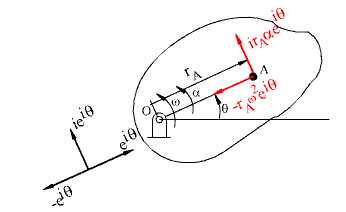
Hız vektörünün türevi yerdeğişimin zamana göre ikinci türevini verecektir:

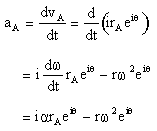
Burada cismin açısal ivmesidir. Açısal ivme, konum açısının zamana göre ikinci türevi; saat yelkovanına ters yönde olduğunda pozitif sayılacaktır. Saat yelkovanı yönünde ise negatif açısal ivmedir.

Birinci terimin şiddeti r_A, yönü i olup A₀A ya diktir. Bu vektörün yönü A₀A vektörünün açısal ivme, ya göre 90⁰ döndürülmesi ile elde edilir. Bu ivme bileşeni A noktasının yörüngesine teğet olduğundan teğetsel ivme bileşenidir ve genellikle a_A^t olarak gösterilir. İkinci terimin şiddeti açısal hızın karesi ile A₀A uzaklığının çarpımıdır (r²), yönü ise - birim vektördür, yani r_A konum vektörüne ters yönde bir vektördür. Ayrıca açısal hızın karesi olduğundan yön açısal hız veya ivmeden daima bağımsız olacaktır. Bu ivmeye normal ivme diyeceğiz ve a_Aⁿ ile göstereceğiz (bazı kitaplarda bu ivmeye merkezkaç ivmesi denirse de bu terimin kullanılması yanlış anlamalara neden olduğundan burada kullanılmayacaktır). Normal ivme A noktasının yörüngesine daima dik olup her zaman yörüngenin eğrilik merkezine doğrudur. Sabit bir eksen etrafında dönen cisimlerin üzerinde bulunan her hangi bir noktanın hız ve teğetsel ivme yönü açısal hız ve ivmeye bağlı iken normal ivmenin yönü açısal hız ve ivmenin yönünden bağımsızdır.

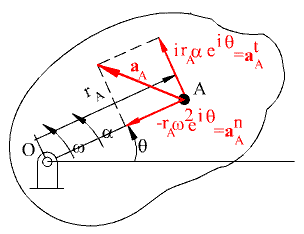
Bu açıklamaların ışığında A noktasının ivmesi iki bileşenle:

a_A = a_A^t + a_Aⁿ

gösterilebilecektir.

t ve n üstel indisleri teğetsel ve normal ivme bileşenlerini göstermek içindir. Bir cismin sabit bir eksen etrafında dönmesi sırasında, dönme ekseninin geçtiği A₀ merkez noktası cisim üzerinde bulunan hızı ve ivmesi sıfır olan tek noktadır.

       Cismin sabit bir eksen etrafında dönmesi sırasında hareket özelliklerini şu şekilde özetleyebiliriz:

1. Cisim üzerinde her noktanın hızı, cismin açısal hızı ile o noktanın dönme eksenine uzaklığının çarpımına eşittir. Yani eksenden uzaklaştıkça hız artacaktır. Hız vektörü daima o noktayı dönme eksenine birleştiren doğruya dik olup yönü açısal hız yönüne göre belirlidir.
2. Cisim üzerinde her noktanın normal ivmesi, açısal hızın karesi ile o noktanın dönme eksenine uzaklığının çarpımıdır. Normal ivme daima o noktadan dönme ekseni merkezine doğrudur.
3. Cisim üzerinde her noktanın teğetsel ivmesi, açısal ivme ile o noktanın dönme eksenine uzaklığının çarpımına eşittir. Teğetsel ivme vektörü, o noktayı dönme ekseni merkezine birleştiren doğruya dik olup yönü açısal ivme yönüne göre belirlenir.
4. Cisim üzerinde bulunan bir noktanın ivmesi teğetsel ve normal ivmelerin vektörel toplamıdır.
5. Cisim belirli bir açısal hız ile dönerken sadece dönme merkezinin açısal hızı ve ivmesi sıfırdır.

Ayrıca dikkat edilir ise, açısal hız ve ivme bir cisme ait değerlerdir (cismin üzerinde bir noktaya ait değer değildirler).

©es