4.1 Hız ve İvme Analizi -2

Genel Düzlemsel Hareket :

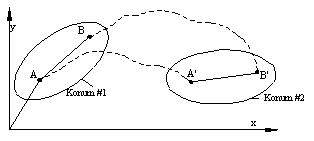
Düzlemde dönme veya öteleme hareketi olarak tanımlanmayan hareket genel düzlemsel harekettir. Genel düzlemsel hareket dönme ve öteleme hareketlerinin birleşimi olan bağıl hareket kavramı kullanılarak ele alınabilir.

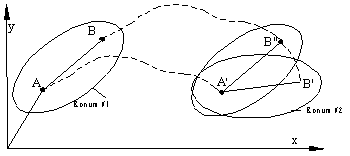
AB konumundan A'B" konumuna öteleme, A'B' konumuna A' merkezli dönme

AB noktaları ile tanımlanan bir cismin düzlemsel hareketini ele alalım. Cismin birinci konumdan ikinci konuma belirli bir Dt zamanında yer değişimi, cismin ilk olarak AB konumundan bir ara konum olan A'B" konumuna ötelemesi ve A' noktasından geçen düzleme dik bir eksen etrafında dönerek A'B' konumuna gelmesi olarak ele alınabilir. Yani genel hareket dönme ve öteleme hareketlerinin süperpozisyonudur. AB konumu ile A'B' konumu arasında hareket sadece yukarıda açıklandığı şekilde olmayabilir. Örneğin istenir ise AB konumunu A"B' gibi bir ara konuma getirip B' den geçen bir eksen etrafında dönme yaparak son konuma erişilebilir, veya ilk olarak A noktasından geçen bir eksen etrafında dönülerek AB" A'B' ne paralel konuma getirildikten sonra öteleme yapılarak son konuma geçilebilir Noktaların gerçek yörüngeleri sonlu yakın konumlarda bu hareketlerle aynı olmayacağı tabiidir. Ancak bu iki konum birbirlerine sonsuz yakın duruma geldiğinde, bu hareketler arasında fark kalmayacaktır.

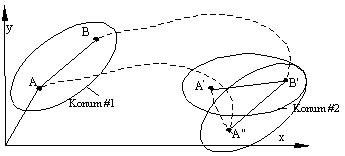
AB konumundan A"B' konumuna öteleme, A'B' konumuna B' merkezli dönme

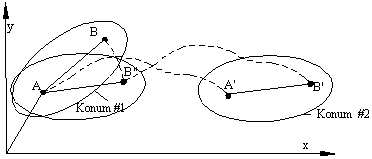
AB konumundan AB" konumuna A merkezli dönme, A'B' konumuna öteleme

Cisim öteleme yaparken her nokta cisim üzerinde seçilen bir noktanın hız ve ivmesi ile hareket edecektir. Cismin dönme yapması sırasında ise, cisim seçilen noktadan geçen düzleme dik bir eksen etrafında dönerken, seçilen nokta konumunu değiştirmeyecek, diğer noktalar bu noktaya göre bir dairesel hareket yapacaktır. Seçilmiş olan nokta sabit bir nokta değildir ve bu nedenle cismin bu noktaya göre hareketi bağıl harekettir.

Hareketi incelemek için hareketli düzlem üzerinde A noktasından geçen, sabit koordinat eksenine paralel bir x-y koordinat eksenini yerleştirelim. Öteleme sırasında bu koordinat ekseni sabit koordinat eksenine (X-Y) paralel kalır.

Cismin AB konumundan A'B' konumuna geçişi iki etapta olduğu kabul edilecektir. Birinci etapta hareket AB konumundan A'B" konumuna her noktanın r_A yer değişimi olacak şekilde ötelemesidir. Öteleme A noktasının toplam hareketi kadardır. Bu aynen (a) kısmında ele almış olduğumuz rijit cismin ötelemesidir . İkinci olarak cismin A' den geçen düzleme dik bir eksen etrafında açısı kadar dönmesidir. Cismin rijit olması nedeni ile cismin üzerinde bulunan B noktası B" konumundan B' konumuna giderken AB uzunluğu sabit olacağından B', A' merkezli BA yarıçaplı bir daire yayı üzerinde olacaktır ve B noktası A noktasına göre r_B/A kadar konumunu değiştirecektir. Bu hareket B noktasının A noktasına göre bağıl hareketidir.

B noktasının toplam yer değişimi bu iki yer değişimin vektörel toplamıdır:

      r_B = r_A +r_B/A

B" den B'ne hareket bir dönme hareketi olduğundan, r_B/A= |BA| olacaktır. Bu bağıl hareketin o andaki mutlak açısal dönmenin fonksiyonu olduğuna dikkat edelim. Seçmiş olduğumuz A, B noktaları değişse bile aynı kalacaktır ve bu açı cismin birinci konumu ile ikinci konumu arasında kalan dönme açısıdır. Bu nedenle değişik A noktası seçimi bu açısal dönmeyi etkilemeyecektir. Aynı şekilde, dönme ve öteleme hareketlerinin sırası değiştirilse, dönme açısı yine aynıdır. Yer değişim bir zaman içinde olduğundan elde edilen denklemi bu zaman aralığına böldüğümüzde ve bu zaman aralığının limitte sıfır olduğunu düşündüğümüzde:

      V_B = V_A + V_B/A

olur. Bu denklemde:

      V_B/A =x r_B/A

cismin açısal hızı ve:

      r_B/A = AB = r_B - r_A (B noktasının A noktasına göre bağıl konumu)

dur. v_B/A cismin üzerinde bulunan A ve B noktaları arasında bağıl hız dır. v_B ve v_A A ve B noktalarının mutlak hız larıdır.

Aynı sonucu kompleks sayılarla elde etmemiz mümkündür. B noktasının konumunu A noktasının konum vektörü kullanılarak yazdığımızda:

      r_B = r_A +b

burada b= |AB| ve ise AB doğrusu ile referans eksenimizin reel pozitif yönü ile yaptığı açıdır (saat yelkovanına ters yön pozitif kabul edilecektir). bterimi B noktasının A noktasına göre konumunu gösteren bağıl konum vektörü dür. A ve B noktaları aynı cisimde olduklarından b uzunluğu sabittir. Bağıl hareketle ilgilendiğimizden; A noktasının konumunu, hızını ve ivmesini bildiğimizi kabul edelim (v_A ve a_A biliniyor). r_B konum vektörü denkleminin zamana göre türevini aldığımızda:

      v_B = v_A +ib

dir. Burada = d/ dt dir. İkinci terimin şiddeti b dır ve yönü i birim vektörü yönündedir. Bu birim vektör AB doğrusuna dik ve AB nin açısal hız vektörünün yönüne göre 90⁰ saat yelkovanı yönünde veya ters yönünde döndürülmüş bir vektördür. Bu ikinci terim B noktasının A noktasına göre bağıl hızıdır. bu durumda:

      v_B/A = ib (B nin A ya göre bağıl hızı)

ve

      v_B= v_A+ v_B/A (B noktasının mutlak hızı)

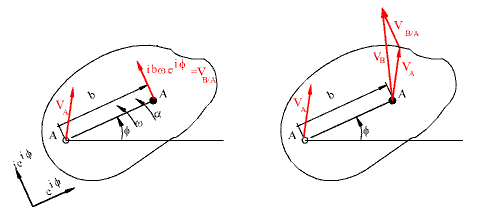
Hız denkleminin zamana göre türevi B noktasının ivmesini verecektir:

      a_B = a_A +ib -b²

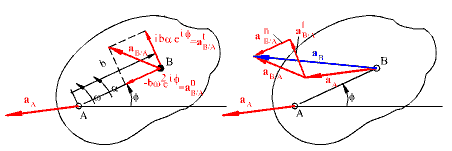
Bağıl hızın türevinden elde edilen birinci terimin şiddeti ba ve yönü i dır. Bu yön AB doğrusuna diktir. Bu bağıl ivmeye teğetsel bağıl ivme diyeceğiz ve a^t_B/A olarak göstereceğiz. Bağıl hızın türevinden elde edilen ikinci terimin ise şiddeti b² olup yönü - dir. Bu yön AB yönünde olup dönme ekseni üzerinde olan A noktasına doğrudur. Bu yön B noktasının A ya göre bağıl yörüngesine diktir ve normal bağıl ivme olarak adlandırılarak aⁿ_B/A şeklinde gösterilecektir. B noktasının ivmesi:

      a_B = a_A + a^t_B/A + aⁿ_B/A

ve

      a_B/A = a^t_B/A + aⁿ_B/A

Bu durumda, genel düzlemsel hareket durumunda bir cismin üzerinde bulunan iki noktanın birbirlerine göre bağıl hareketi bu noktalardan birine göre diğer noktaların dönmesi olarak incelenebileceğini ve bağıl hız ve ivme terimlerinin bir nokta etrafında dönme gibi elde edilebileceğini söyleyebiliriz.

İkinci farklı bağıl hareket ise bir hareketli cismin diğer bir hareketli cisme göre öteleme yapmasıdır. İki rijit cisim üzerinde bulunan ve ani çakışan iki noktayı ele alalım. Bir cismin üzerinde bulunan bir noktanın diğer cisim üzerinde yörüngesini bildiğimizi kabul edelim.

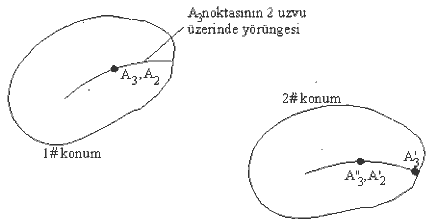
2 numaralı düzlemin 1# konumundan hareket ederek 2# konuma geldiğini ve bu sırada A₂ noktasına 1# konumda çakışık olan A₃ noktasının 2 uzvuna göre bağıl hareket yaparak, A₂ noktasının 2# konumuna (A'₂) gelmesi sırasında A'₃ noktasına geldiğini düşünürsek; birinci konumda çakışık olan iki nokta ikinci konumda çakışık olmayacak (A'₂ ve A'₃ ) , farklı konumlarda bulunacaklardır. A₃ noktasının 2 uzvu üzerinde yörüngesi bilindiğine göre, bu noktanın hareketinin iki kısımdan oluştuğunu düşünmemiz mümkündür. Bu hareketlerden birisi A₃ noktasının 2 uzvu ile birlikte hareketi, bu durumda A₃ ten A"₃ ne hareket (A"₃ ve A'₂ çakışık) , ikincisi ise, 2 cismine göre A"₃ den A'₃ e hareketdir (bu sırada 2 cisminin hareketi yoktur). Bu iki hareketin sırası önemli değildir. Şekilde görüldüğü gibi, A₃ noktası ilk olarak A₂ ile aynı hareketi yapacak, yani r_A2 kadar yer değiştirecek, daha sonra 2 cismine göre r_A3/2 kadar yer değiştirecektir. A₃ ün toplam yer değiştirmesi bu iki yer değiştirmenin toplamıdır.

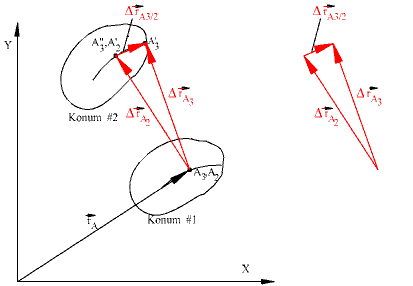
A₃ noktasının toplam yer değişimi:

      r_A3 = r_A2 +r_A3/2

Birinci konumdan ikinci konuma geçiş belirli bir t zaman aralığında olacağından, yer değişim vektörlerini t ye böler ve limitte t sıfır alınır ise:

      v_A3 = v_A2 + v_A3/2

Hız denklemi elde edilecektir. Bu denklemde v_A3/2, A₃ noktasının 2 cismine göre bağıl hız vektörüdür ve daima bu noktanın 2 cismine göre bağıl yörüngesine teğettir.

Mekanizmalarda bu tip bağıl hareket iki hareketli uzuv arasında bir kayar mafsal, kamalı silindir mafsalı veya kam çifti olduğunda söz konusudur. Kam çiftlerinin incelemesi eşdeğer mekanizma kavramı ile yapılır. Kayar mafsalla birleştirilen iki uzuv arasında bağıl hareket sırasında bir uzuv üzerinde bulunan herhangi bir noktanın diğer uzuv üzerinde yörüngesi, mafsal ekseni yönünde bir doğrudur. Kamalı silindirde ise, bir uzvun silindir ekseni üzerinde alınan bir noktasının diğer uzva göre yörüngesi bir doğrudur.

İki uzuv arasında bağıl hareketi açıklamak için birbirleri ile kayar mafsalla bağlı 2 ve 3 uzuvlarını ele alalım. Ayrıca (basit bir hareket olması için) 2 uzvu sabit uzva bir döner mafsalla bağlı olsun. B hem 2 ve hemde 3 uzvu üzerinde bulunan iki ayrı çakışan B₂ ve B₃ noktalarıdır. B noktası için (B₂ veya B₃ ) kompleks sayılar ile konum vektörü yazıldığında:

      R_B = r

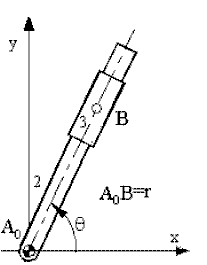
R_B hem B₂ ve hemde B₃ için konum vektörüdür. Ancak B₂ için r sabit olacaktır. B₃ için ise r değişken bir uzunluktur. Bu nedenle, çakışan noktalar olduğundan B₂ ve B₃ noktalarının konum vektörleri aynı isede, türev alındığında hız vektörleri aynı olmayacaktır. Türev alınırken hangi noktanın hızını bulmak istiyorsak ona göre r uzunluğunun zamana göre değişimi vardır veya yoktur. Örneğin B₂ noktasının zamana göre değişimi incelenecek ise:

      v_B2= ir

burada = d/ dt, 2 uzvunun açısal hızıdır. Eğer B₃ noktasının zamana göre değişimi incelenecek ise:

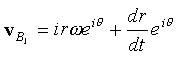
Birinci terim V_B2 yani B₂ noktasının hızıdır. İkinci terim ise B₃ noktasının 2 uzvuna göre bağıl hızıdır. Bu hız bağıl yörünge yönündedir. Bu durumda:

      v_B3 = v_B2 + v_B3/2

B₂ ve B₃ noktalarının hızlarının farklı olmasından dolayı B₃ bir an sonra 2 uzvu üzerinde farklı bir B'₂ noktası ile çakışacaktır.

r_B3 konum vektörünün zamana göre ikinci türevi alındığında:

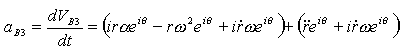
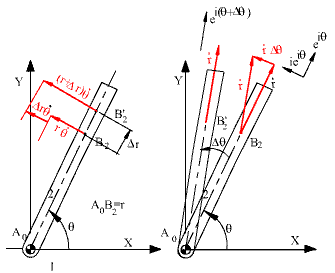
Birinci parantez içinde bulunan terimler v_B2 hız vektörünün türevi, ikinci parantezdeki terimler ise bağıl hız vektörü v_B3/2 nin türevidir. Dikkat edilir ise, birinci parantezdeki ilk iki terim (ir - r²) r sabit olarak alındığında elde edilecek olan terimlerdir. Bu iki terim r nin sabit olduğu durumda ikinci türev için elde edilecek terimlerdir, B₂ noktasının teğetsel ve normal ivmeleri olup toplamı B₂ noktasının ivmesini (a_B2) verir. Birinci parantezdeki son terim ise, B₃ ile çakışan B₂ noktasının artık çakışmıyor olması ve ayrı bir B'₂ noktası ile çakışıyor olmasıdır. t zaman aralığı içinde B₃ noktası B₂ noktasından r kadar kayar çift ekseni yönünde uzaklaşacak ve B'₂ noktası ile çakışacaktır. B₂ noktasının hızı (ir) iken B'₂ noktasının hızı i(r +r)dır. Bu t zaman aralığında hız değişimi farkı ise (ir)dır. Bu terim t ye bölünür ve limitte t sıfır olur ise kayar çift eksenine dik ve şiddeti olan ivme bileşkesi bulunur.

Bağıl hız vektörünü gösteren terimin türevini alınca elde ettiğimiz terimleri inceleyelim. İkinci parantezde birinci terim () bağıl hızın şiddetinin değişimi ile ilgilidir ve yönü bağıl yörüngeye teğettir. İkinci terim (i) ise bağıl hız vektörünün yönünün değişmesinden dolayıdır. Bunu açıklamak için bağıl hızın sabit olduğunu düşünelim. Bir t zaman aralığında 2 uzvu kadar A₀ etrafında dönecektir. Bağıl hızın yönü bu dönme ile birim vektör yönünde iken birim vektör yönünde olacaktır. Şekilde görüldüğü gibi, bağıl hız vektörünün (i) kadar değişimi ile sonuçlanır ve bu terimin t zaman aralığına bölünüp t sıfıra giderken limiti alındığında, (i) ivme vektörü bileşkesi elde edilir. Bu terim bağıl yörünge eksenine dik olup şiddeti ise bağıl hız ile açısal hızın çarpımına eşittir. Dikkat edilir ise, a_B3 ivme denkleminde bulunan iki parantezde son terimler farklı nedenlerle elde edilmiş olmalarına rağmen, gerek yön ve gerek şiddet açısından aynı terimlerdir. Bu durumda bu iki terim 2iolarak birleştirilebilir. Bu terim Corriolis ivme bileşeni olarak adlandırılmaktadır ve a^c_B3/2 olarak gösterilir. Coriolis ivme bileşeni bir bağıl ivme bileşenidir. Şiddeti açısal hız ile bağıl hızın çarpımının iki katı olup yönü ise bağıl hız vektörünün açısal hız yönünde 90⁰ döndürülmesi ile elde edilir Böylece B₃ noktasının ivmesi :

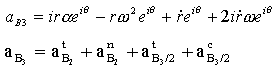
KAYAR ÇİFT EKSENİNİN RADYAL YÖNDE OLMADIĞI DURUM

Yukarıda ele alınan durumda kayar çift eksen yönü B₀B radyal yön ile çakıştığından, B₂ noktasının normal ivmesi (aⁿ_B2) ile bağıl teğetsel ivme (a^t_B3/2) ve B₂ noktasının teğetsel ivmesi ile Corriolis ivmesi yönleri (a^c_B3/2 ve a^t_B2)aynı bulunmaktadır. Daha genel bir durum için aşağıda gösterilen durumu ele alalım. Bu şekilde görüldüğü gibi 2 ve 3 uzuvları arasında bulunan kayar çift genel bir yöndedir. B₃ konum vektörü:

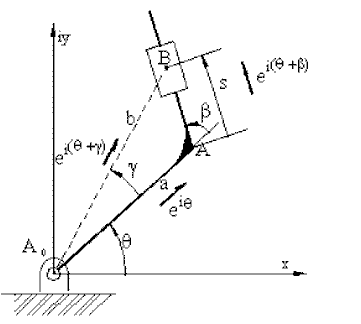
dir. Bu denklemde ve a (=A₀A), 2 uzvunun sabit boyutları olup, s ise B₂ için sabit, B₃ için değişkendir. Türev alındığında:

Bu denklem:

şeklinde yazılabilir. Dikkat edilir ise:

dir. Burada b, A₀B uzunluğu olup değişkendir. ise 2 uzvu üzerinde bulunan A₀A ile A₀B doğruları arasında kalan değişken açıdır. Ancak 2 uzvu üzerinde sabit B₂ noktası göz önüne alındığında, bu nokta için b ve sabit değerlerdir. Bu durumda B₃ noktasının hızı:

veya

      v_B3 = v_B2 + v_B3/2

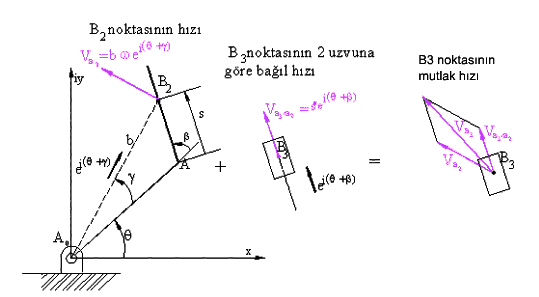
Birinci terimin şiddeti |A₀B| =b olup yönü B noktasını dönme merkezine bağlayan A₀B doğrusuna diktir (yönü). İkinci terimin şiddeti olup B₃ noktasının 2 uzvuna göre bağıl hızıdır. Bu bağıl hız vektörünün yönü ise kayar çift ekseni yönü olan AB yönüdür ve birim vektörle gösterilir.

Hız denkleminin türevi alındığında B₃ noktasının ivmesi elde edilecektir:

Terimler guruplanır ise:

veya hız denkleminde olduğu gibi, dersek:

İlk iki terim B₂ noktasının teğetsel ve normal ivmeleridir ve bu ivmelerin yönü sırası ile A₀B doğrusuna dik ve paraleldir (A₀' a doğru). Üçüncü terim ise bağıl Corriolis ivmesi olup 2 ve 3 uzuvları arasında bulunan kayar mafsal eksenine (AB doğrusuna), dikdir (birim vektörü i dir). Sonuncu terim ise bağıl teğetsel ivme olup şiddeti yönü ise birim vektörü yönünde, yani AB doğrusu yönündedir. Bu durumda B₃ noktasının ivmesi:

dir.

©es