4.2 Mekanizmalarda Hız ve İvme Analizi -1
Mekanizmalarda hız ve ivme analizi vektörel olarak bağıl hız ve ivme
kavramı ile yapılır. Genel olarak verilen değerler ile başlanılır ve A,B,C,…
gibi genellikle mafsal eksenlerinin geçtiği noktalar sırası ile kullanılarak
analiz gerçekleştirilir.
Elde edilecek olan hız denklemleri:
VB = VA + VB/A
VC = VB + VC/B
ve benzeri denklemler olacaktır. İvme için ise, benzer şekilde:
aB = aA + atB/A + anB/A
aC = aB + atC/B + anC/B
veya aD4 = aD3 + atD4/D3 + aCD4/D3
benzer denklemler yazılacaktır. Seçilen A,B,C,D noktalarının mümkün olduğunca döner mafsal ekseni üzerinde olmasının en önemli nedeni mafsal ekseninde olan bu noktanın mafsalla birleştirilen iki uzuv üzerinde daima çakışan nokta olmasıdır. Daima çakışan bu noktalar arasında bağıl hız ve ivme olmayacağından (sıfır olacağından) dolayı her iki uzuvdada bu noktaların hız ve ivmesi eşit olacaktır. Bu nedenle genel kural olarak bir uzvun üzerinde bulunan her hangi bir noktanın hız ve ivmesini belirlemeden önce bu uzvu diğer uzuvlar ile birleştiren mafsalların merkezlerinde bulunan noktaların hız ve ivmesi bulunmalıdır.
![]() Dikkat
edilmesi gereken diğer bir önemli nokta ise, konum hız ve ivme analizi
sıra ile yapılabilir. Konum analizi yapılmadan hız analizi,
konum ve hız analizi yapılmadan ivme analizi yapılamaz. Bunun nedeni,
hız ve ivmelerin belirlenmesi sırasında gerekli olan yönler konum analizi
ile belirlenecek, ivme analizi için normal ve Coriolis ivmesi terimleri
sadece hız analizinde elde edilen terimlerin fonksiyonu olacaktır.
Dikkat
edilmesi gereken diğer bir önemli nokta ise, konum hız ve ivme analizi
sıra ile yapılabilir. Konum analizi yapılmadan hız analizi,
konum ve hız analizi yapılmadan ivme analizi yapılamaz. Bunun nedeni,
hız ve ivmelerin belirlenmesi sırasında gerekli olan yönler konum analizi
ile belirlenecek, ivme analizi için normal ve Coriolis ivmesi terimleri
sadece hız analizinde elde edilen terimlerin fonksiyonu olacaktır.
Devre kapalılık denklemleri hız ve ivme analizi için kolaylıkla kullanılabilir çünkü, bu denklemlerde mekanizmada bulunan tüm değişkenler yer almaktadır. Devre kapalılık denklemlerinin zamana göre birinci ve ikinci türevleri alındığında, ve konum değişkenlerinin birinci ve ikinci türevlerine göre çözüm yapıldığında bu değerler her hangi bir noktanın hız ve ivmesinin belirlenmesi için gerekli tüm terimleri belirleyecektir. Vektör devre denkleminin zamana göre birinci türevi bize "Vektörel Hız devre denklemini", ikinci türevi ise "Vektörel İvme devre denklemini" verecektir. Eğer konum değişkenleri vektör devre denklemi kullanılarak çözülmüş ise, vektör hız denklemleri konum değişkenlerinin birinci türevlerine göre (bu değişkenlere hız değişkenleri diyeceğiz) ve vektör ivme denklemleride konum değişkenlerinin ikinci türevine göre (bu değişkenlere ivme değişkenleri diyeceğiz) lineer bir denklem takımı oluşturacaktır. Hız ve ivme değişkenleri bu denklemlerden çözüldükten sonra herhangi bir uzvun üzerinde her hangi bir noktanın hız ve ivmesi kolaylıkla bulunacaktır.
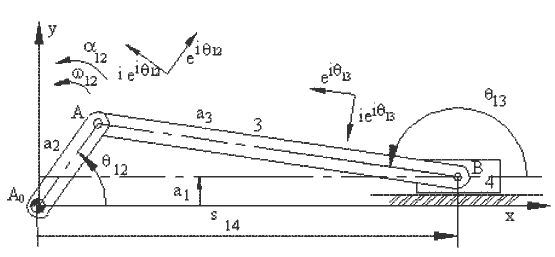
İlk örnek olarak şekilde gösterilen krank-biyel mekanizmasını ele alalım.
Giriş kolunun (2 uzvu) yatay ile yaptığı açı, ![]() 12,
açısal hızı
12,
açısal hızı ![]() ve açısal ivmesi
ve açısal ivmesi ![]() verildiği kabul edilmektedir. Devre kapalılık denklemi ve eşleniği kompleks
sayılar ile yazıldığında:
verildiği kabul edilmektedir. Devre kapalılık denklemi ve eşleniği kompleks
sayılar ile yazıldığında:
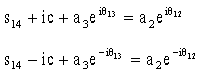 |
(1a) (1b) |
Verilen bir ![]() 12
değerine göre x ve
12
değerine göre x ve ![]() 13
konum değişkenlerinin nasıl bulunduğu bir önceki kısımda incelenmişti.
Burada bu denklemlerin zamana göre birinci türevini alarak vektör hız
devre denklemi ve eşleniğini elde edelim.
13
konum değişkenlerinin nasıl bulunduğu bir önceki kısımda incelenmişti.
Burada bu denklemlerin zamana göre birinci türevini alarak vektör hız
devre denklemi ve eşleniğini elde edelim.
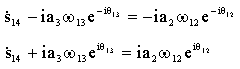 |
(2a) (2b) |
Bu denklemlerde ![]() hız değişkenleridir. 2 denklemi dikkatli bir şekilde incelendiği takdirde
bu vektör denkleminin:
hız değişkenleridir. 2 denklemi dikkatli bir şekilde incelendiği takdirde
bu vektör denkleminin:
vB + vA/B = vA
bağıl hız denkleminden farklı bir denklem olmadığı görülecektir. Bu denklemin
pratik açıklaması, A ve B noktaları 3 uzvunda bulunan 2 nokta olduğu gibi
mafsal merkezleri olduklarından dolayı A noktası aynı zamanda 2 uzvunda
ve B noktası 4 uzvunda bulunan noktalarla daima çakışan noktalardır. Öyle
ise vA2=vA3=vA.
ve vB3=vB4=vB
dir. 2 uzvunu ele aldığımızda bu uzuv sabit eksen etrafında dönme yaptığından
A noktasının hızı AA0 doğrusuna dik
yönde (![]() 12'ye
göre) ve şiddeti
12'ye
göre) ve şiddeti ![]() 12|AA0|=
12|AA0|=
![]() 12a2
olan bir vektördür. 3 uzvu dikkate alındığında, A noktasının hızı B noktasının
hızı ve bağıl hız ile ifade edildiğinde: vA3
= vB + vA/B
= vA olacaktır. Bu denklemde vA/B
A noktasının B noktasına göre bağıl hızı olup, AB doğrusuna diktir ve
şiddeti
12a2
olan bir vektördür. 3 uzvu dikkate alındığında, A noktasının hızı B noktasının
hızı ve bağıl hız ile ifade edildiğinde: vA3
= vB + vA/B
= vA olacaktır. Bu denklemde vA/B
A noktasının B noktasına göre bağıl hızı olup, AB doğrusuna diktir ve
şiddeti ![]() 13a3
dir. B noktası 3 ve 4 uzuvlarında daima çakışan iki noktadır ve 4 uzvu
üzerinde bulunan B noktasının yörüngesi 1 ve 4 uzuvları arasında bulunan
kayar mafsaldan dolayı, kayar mafsal eksenine paralel bir doğrudur. Bu
durumda vA hız vektörünün gerek
şiddeti ve gerek yönü bilinmekte, vB
ve vA/B vektörlerinin ise yönleri
bilinmektedir (vB kayar mafsal
eksenine paralel ve vA/B AB doğrusuna
diktir). Bu durumda vB ve vA/B
hız vektörlerinin şiddeti bilinmemektedir. Bu bilinmeyenler hız devre
denkleminde
13a3
dir. B noktası 3 ve 4 uzuvlarında daima çakışan iki noktadır ve 4 uzvu
üzerinde bulunan B noktasının yörüngesi 1 ve 4 uzuvları arasında bulunan
kayar mafsaldan dolayı, kayar mafsal eksenine paralel bir doğrudur. Bu
durumda vA hız vektörünün gerek
şiddeti ve gerek yönü bilinmekte, vB
ve vA/B vektörlerinin ise yönleri
bilinmektedir (vB kayar mafsal
eksenine paralel ve vA/B AB doğrusuna
diktir). Bu durumda vB ve vA/B
hız vektörlerinin şiddeti bilinmemektedir. Bu bilinmeyenler hız devre
denkleminde ![]() 13
ve
13
ve ![]() 13a3
değerleridir.
13a3
değerleridir.
Eğer devre denklemini grafik olarak çözmek istersek, denklemin her bir tarafında bir bilinmeyenin olması daha uygun olacaktır (analitik çözümlerde, genellikle bilinen terimler denklemin sağına bilinmeyen terimler solunda bulunması istenilir). Bu durumda hız devre denklemi:
![]()
olarak yazılacaktır. Bu denklem vektörel olarak:
vB = vA + vA/B
dır ve dikkat edilir ise:
![]()
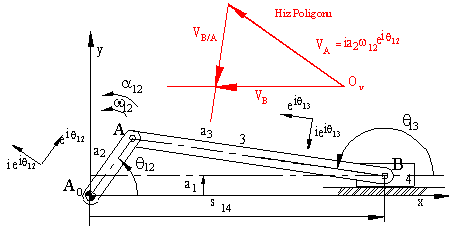
Bilinmeyen değerlerin grafik çözümü için ilk olarak vA
hız vektörünün şiddeti, |vA|=
![]() 12|AA0|=
12|AA0|=
![]() 12a2
bulunur. Belirli bir kv ölçeği
kullanılarak (birimi mm/(mm/s)dir) uzunluğu vA
vektörü şiddetine orantılı, yönü vA
vektörü yönünde olan (bu yön A0A doğrusuna
diktir) bir doğru (vektör) çizilir. Kullanılan ölçekten dolayı, şiddet
ölçüsü uzunluk birimidir. Bu vA
vektörünün başlangıç noktasından vB
vektörü yönünde (ki bu kayar mafsal ekseni yönüdür) bir doğru, bitiş noktasından
ise vA/B vektörü yönünde bir
doğru (ki bu yön BA doğrusuna diktir) çizilir. Bu iki doğrunun kesiştikleri
nokta vB ve vA/B
vektörlerinin şiddetini ve yönlerini bize verecek, elde edilen üçgende
vB = vA
+ vA/B denklemi sağlanmış olacaktır.
Bu şekle hız vektör çokgeni denmektedir.
Bu vektörlrin uzunluklarını ölçer, kv
ölçeği ile böler isek, hız şiddetlerini belirlemiş oluruz. Örneğin
12a2
bulunur. Belirli bir kv ölçeği
kullanılarak (birimi mm/(mm/s)dir) uzunluğu vA
vektörü şiddetine orantılı, yönü vA
vektörü yönünde olan (bu yön A0A doğrusuna
diktir) bir doğru (vektör) çizilir. Kullanılan ölçekten dolayı, şiddet
ölçüsü uzunluk birimidir. Bu vA
vektörünün başlangıç noktasından vB
vektörü yönünde (ki bu kayar mafsal ekseni yönüdür) bir doğru, bitiş noktasından
ise vA/B vektörü yönünde bir
doğru (ki bu yön BA doğrusuna diktir) çizilir. Bu iki doğrunun kesiştikleri
nokta vB ve vA/B
vektörlerinin şiddetini ve yönlerini bize verecek, elde edilen üçgende
vB = vA
+ vA/B denklemi sağlanmış olacaktır.
Bu şekle hız vektör çokgeni denmektedir.
Bu vektörlrin uzunluklarını ölçer, kv
ölçeği ile böler isek, hız şiddetlerini belirlemiş oluruz. Örneğin ![]() 13
=d(
13
=d(![]() 13)/dt
açısal hızı bulmak için ilk olarak okunan vA/B
uzunluğu kv ile bölünerek hız
şiddeti bulunduktan sonra, vA/B
=
13)/dt
açısal hızı bulmak için ilk olarak okunan vA/B
uzunluğu kv ile bölünerek hız
şiddeti bulunduktan sonra, vA/B
= ![]() 13a3
olduğundan ve a3=|AB| olduğundan, açısal
hız
13a3
olduğundan ve a3=|AB| olduğundan, açısal
hız ![]() 13=|vA/B|
/a3 denklemi kullanılarak belirlenebilir.
Açısal hızın yönünü bulmak için ise, bulunan vA/B
hız vektörü yönü kullanılarak karar verilebilir. Örneğin Şekilde vA/B
hız vektörü aşağıya doğru olduğundan ve bu vektörde B noktasının A noktasına
göre bağıl hızı incelendiğinden, 3 uzvunun saat yelkovanı yönünde bir
açısal hızı olduğu görülecektir.
13=|vA/B|
/a3 denklemi kullanılarak belirlenebilir.
Açısal hızın yönünü bulmak için ise, bulunan vA/B
hız vektörü yönü kullanılarak karar verilebilir. Örneğin Şekilde vA/B
hız vektörü aşağıya doğru olduğundan ve bu vektörde B noktasının A noktasına
göre bağıl hızı incelendiğinden, 3 uzvunun saat yelkovanı yönünde bir
açısal hızı olduğu görülecektir.
Eğer bilinmeyen bağımlı konum değişkenleri verilen bir bağımsız konum
değişkeni değerine göre çözülmüş ise, (x ve ![]() 13
değerleri verilen bir
13
değerleri verilen bir ![]() 12
değerine göre biliniyor ise) hız devre denklemi daima hız değişkenleri
arasında (
12
değerine göre biliniyor ise) hız devre denklemi daima hız değişkenleri
arasında (![]() 12,
12,
![]() 13
ve
13
ve ![]() 14
değişkenleri) bir lineer ilişkiyi belirleyecektir. Giriş açısının zamana
göre değişimi,
14
değişkenleri) bir lineer ilişkiyi belirleyecektir. Giriş açısının zamana
göre değişimi, ![]() 12
, bilniyor ise, Hız devre denkleminden bilinmeyen bağımlı iki hız değişkeni
12
, bilniyor ise, Hız devre denkleminden bilinmeyen bağımlı iki hız değişkeni
![]() 13
ve
13
ve ![]() 14
lineer cebir kuralları kullanılarak 2a ve 2b denklemlerinden kolayca çözülebilir.
Genellikle iki bilinmeyenli iki denklem olduğundan Cramer kuralı kullanıldığında:
14
lineer cebir kuralları kullanılarak 2a ve 2b denklemlerinden kolayca çözülebilir.
Genellikle iki bilinmeyenli iki denklem olduğundan Cramer kuralı kullanıldığında:
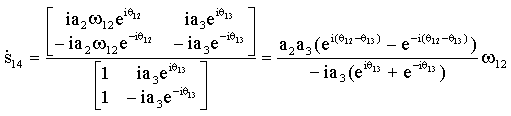
veya
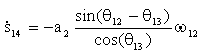 |
(4) |
ve
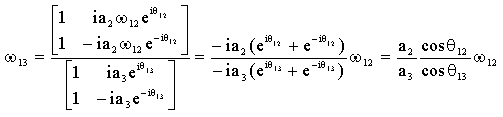 |
(5) |
Dikkat edilir ise, kompleks sayılarla yazılmış hız denklemi ve eşleniği kullanılmak yerine, istenildiğinde vektör hız denkleminin x ve y bileşenleri (kompleks sayılarla yazılmış hız devre denkleminin reel ve sanal kısımları) ayrı ayrı eşitlenerek iki skaler denklem elde edilerek de bilinmeyen hız değişkenleri için çözüm yapılabilecektir. Örneğin krank biyel mekanizması için bu skaler denklemler:
|
(6) |
ve
|
(7) |
dir. Bu iki denklem kullanılarakda ![]() 13
ve
13
ve ![]() 14
için aynı denklemler (4 ve 5 denklemleri) elde edilebilir. Hangi yöntem
kullanılırsa kullanılsın, sonuçta hız değişkenlerini veren denklemler
reel denklemler olmaları gerekir (
14
için aynı denklemler (4 ve 5 denklemleri) elde edilebilir. Hangi yöntem
kullanılırsa kullanılsın, sonuçta hız değişkenlerini veren denklemler
reel denklemler olmaları gerekir (![]() 13
açısal hız değeri kompleks bir değer olamaz).
13
açısal hız değeri kompleks bir değer olamaz).
İvme analizi için en kolay yöntem hız devre denkleminin zamana göre türevi alınarak, hız değişkenlerinin zamana göre türevi olan ivme değişkenlerini içeren ivme devre denkleminin elde edilmesidir. Örneğin yukarıda verilmiş olan krank-biyel mekanizması için devre kapalılık denkleminin türevi olan 2a ve 2b hız devre denklemlerinin zamana göre türevleri alındığında:
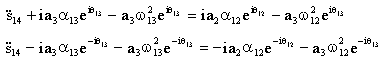 |
(8-a) (8-b) |
denklemleri elde edilir bu denklemlerde ivme değişkenleri:![]() dir.
Dikkat edilir ise kompleks sayı ile yazılmış olan bu denklem vektörel
olarak:
dir.
Dikkat edilir ise kompleks sayı ile yazılmış olan bu denklem vektörel
olarak:
![]()
dir. İvme devre denklemleri ivme değişkenlerine (![]() 12,
12,
![]() 13
ve
13
ve ![]() 14)
göre daima lineer bir denklem takımı oluşturur. Eğer giriş kolunun açısal
ivmesi
14)
göre daima lineer bir denklem takımı oluşturur. Eğer giriş kolunun açısal
ivmesi 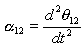 biliniyor ise, 8a ve 8b denklemleri kolaylıkla bilinmeyen ivme değişkenleri
biliniyor ise, 8a ve 8b denklemleri kolaylıkla bilinmeyen ivme değişkenleri
![]() 13
ve
13
ve ![]() 14
için çözülebilir. Örneğin Cramer kuralı kullanılarak
14
için çözülebilir. Örneğin Cramer kuralı kullanılarak ![]() 13
:
13
:
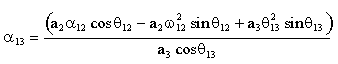 |
(9) |
![]() 14
ise denklem 8a nın reel kısmından:
14
ise denklem 8a nın reel kısmından:
|
(10) |
olarak elde edilir. Bir başka yaklaşım ise hız değişkenleri denklemlerinin
zamana göre türevlerinin alınmasıdır. Örnek olarak denklem 4 ve 5 de verilmekte
olan hız denklemlerinin zamana göre türevleri alındığında, ivme değişkenleri
elde edilecektir. 5 denkleminin türevi alındığında doğrudan elde edilen
3 uzvunun açısal ivmesi, ![]() 13:
13:
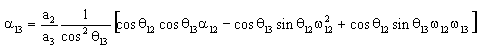
olacaktır. Benzer bir şekilde 4 denkleminin türevi alındığında 4 uzvunun lineer öteleme ivmesi:
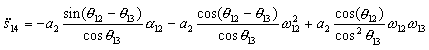
olarak elde edilir. Elde edilen denklemde terimler 9 ve 10 numaralı denkleme
göre farklıdır. İşlemler doğru olarak yapıldığı takdirde, gerekli eşitlikler
kullanılırsa, ![]() 13
ve
13
ve ![]() 14
ü veren denklemlerin birbirine eşit olduğu gösterilebilir. Denklemler
kullanıldığında aynı bağımsız parametre değerlerine göre mutlaka aynı
sayısal sonuç alınacaktır.
14
ü veren denklemlerin birbirine eşit olduğu gösterilebilir. Denklemler
kullanıldığında aynı bağımsız parametre değerlerine göre mutlaka aynı
sayısal sonuç alınacaktır.
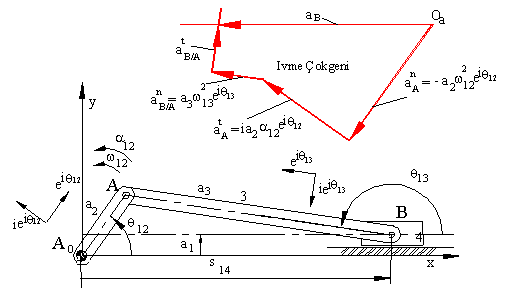
Grafik olarak çözüm için ivme devre denklemi vektörel gösterim kullanılarak ve bazı terimlerin yerleri değiştirilerek yazıldığında:
![]()
Bu denklemde aB/A = - aA/B dir. Denklemin bu şekilde yazılmasının tek nedeni grafik çözüm için denklemin her iki tarafında tek bilinmeyen bırakılması içindir. aB ivmesinin şiddeti bir bilinmeyen ve atB/A teğetsel ivmesi şiddeti ise ikinci bilinmeyendir. Giriş uzvu açısal ivmesi bilindiğinden atA teğetsel ivmesi; hız analizi yapıldı ise, hızlar bilindiğinden anA ve anB/A normal ivmeleri hem şiddet ve hem de yön olarak bilinmektedir. İvme şiddetleri için belirli bir ka ölçeği kullanılacaktır (birimi mm/(mm/s2)), ve bu ölçek ile ivme şiddetleri belirli bir uzunluk boyutuna getirilecektir. atA veya anA vektörlerinden başlayarak her iki vektör uç uca çizildiğinde A noktasının ivmesi gösterilmiştir. Bu vektörlerin ucundan bilinen anB/A vektörü aynı ölçek kullanılarak çizilir. Bundan sonra bu uçtan yönü BA doğrusuna dik bir doğru çizilir ise, şiddeti bilinmeyen atB/A vektörü yönünde bir doğru çizilmiş olacaktır (üstteki şekil). B noktasının ivmesi ise kayar mafsal eksenine paralel olmalı ve yukarıda çizilmiş olan vektörlerin vektörel toplamına eşit olmalıdır. Öyle ise, başlangıç noktasından kayar çift eksenine paralel bir doğru çizdiğimizde, AB doğrusuna dik çizilen doğru ile kesiştiği nokta bizim hız devre denklemimizin kapalılığı noktasıdır. Elde edilen şekil ivme poligonu olarak adlandırılır. Bilinmeyen atB/A ve aB ivme şiddetleri şekildeki bu ivmeleri gösteren uzunlukların kullanılmış olan ka ölçeğine bölünmesi ile elde edilir.
Hız ve ivme değişkenlerinin değerleri o konum için elde edildikten sonra, her hangi bir C noktasının hız ve ivmesi, o noktanın konum vektörünün yazılması ve zamana göre bu konum vektörünün türevlerinin alınarak hız ve ivmesinin bulunmasından ibarettir. Şekilde gösterilmiş olan mekanizmada biyel uzvunu genişleterek bir uzuv üzerinde bir C noktasını ele alalım.Şekilde rC konum vektörü:
|
(11) |
C noktasının hız ve ivmesi:
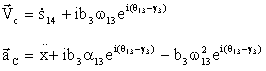 |
(12) (13) |
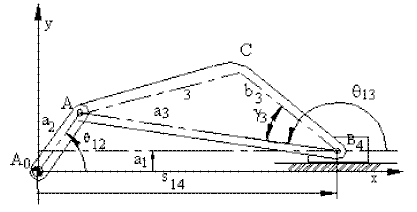
Yukarıda kompleks sayılar ile yazılmış olan denklemler vektörel olarak:
VC
= VB + VC/B
ve
aC
= aB + atC/B
+ anC/B
vektörel hız ve ivme denklemlerinden farklı denklemler değillerdir. Eğer
verilen giriş değerleri ile (![]() 12,
12,
![]() 12
ve
12
ve ![]() 12),
konum değişkenleri (
12),
konum değişkenleri (![]() 13
ve s14), hız değişkenleri (
13
ve s14), hız değişkenleri (![]() 13
ve
13
ve ![]() 14)
ile ivme değişkenleri (
14)
ile ivme değişkenleri (![]() 13
ve
13
ve ![]() 14)
için çözüm yapıldı ise, denklemin sağında bulunan tüm terimler bilinmektedir.
Bu nedenle C noktasının konumu, hızı ve ivmesi kolayca vektörel toplam
yapılarak bulunabilir. C noktasının konumu, hızı ve ivmesi devre kapalılık
denklemi, hız devre denklemi ve ivme devre denklemi çözülmeden belirlenemez.
14)
için çözüm yapıldı ise, denklemin sağında bulunan tüm terimler bilinmektedir.
Bu nedenle C noktasının konumu, hızı ve ivmesi kolayca vektörel toplam
yapılarak bulunabilir. C noktasının konumu, hızı ve ivmesi devre kapalılık
denklemi, hız devre denklemi ve ivme devre denklemi çözülmeden belirlenemez.
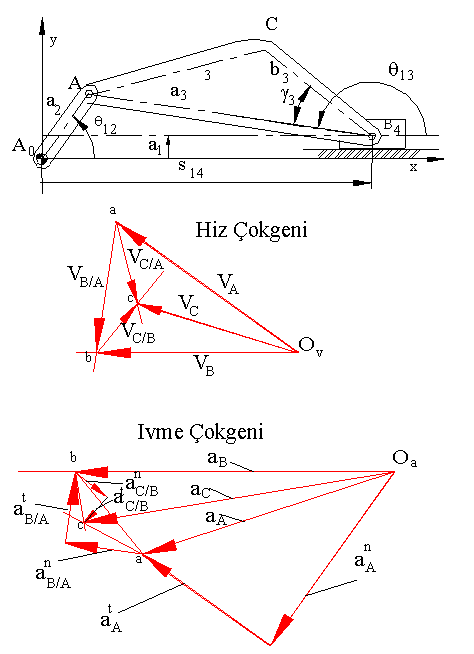
Grafik çözüm için ise, C noktasının hızı ve ivmesi için verilmiş olan denklemdeki vektörler belirli bir ölçek kullanılarak önceden çizilmiş olan hız ve ivme poligonu üzerine çizilerek bulunabilir. Çünkü, C noktasının hız ve ivmesini veren terimler arasında hız ve ivme devre denklemlerini çözdüğümüzde elde etmiş olduğumuz terimler bulunmaktadır. Bu nedenle hız devre denkleminde elde edilmiş olan VB hız vektörünün uç noktasından VC/B hız vektörünü çizdiğimiz takdirde C noktasının hızını bulabiliriz. Benzer bir şekilde ivme devre denklemi için çizmiş olduğumuz ivme poligonu üzerinde bulunan aB ivme vektörünün uç noktasından anC/B ve atC/B ivme vektörlerini arka arkaya çizdiğimizde (sıra önemli değil) aB vektörünün başlangıç noktasının elde edilen son uç noktaya birleştiren doğru bize C noktasının ivmesini verecektir. Alternatif olarak C noktasının konumu, hızı ve ivmesi 3 uzvu üzerinde bulunan B noktası yerine aynı uzuv üzerinde bulunan A noktası kullanılarak yazılabilir. Bu durumda C noktasının konumu, hızı ve ivmesi:
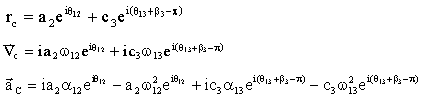
Dikkat edilir ise bu hız ve ivme denklemleri aynı zamanda:
VC
= VA + VC/A
ve
aC
= anA
+ atA
+ atC/A
+ anC/A
vektör denklemleri ile aynıdır.
Hız ve ivme poligonlarında Vektörlerin son uç noktalarını, hızını veya ivmesini gösterdikleri noktaların harfleri ile işaretliyelim (ivme poligonunda A veya C noktasının ivmesi bir kaç vektörün toplamından oluşacağından son çizilen vektörün uç noktası a veya c olarak işaretlenecektir). VA, VB, VC hız vektörlerinin uç noktalarını ve aA, aB, aC ivme vektörlerinin uçlarını birleştirdiğimizde her iki poligonda abc gibi iki farklı üçgen oluşacaktır. Bu üçgenle ilgili olarak önemli bir teorem bulunmaktadır:
![]() Hız
ve ivme poligonunda oluşan abc üçgeni mekanizma uzvunda bulunan A,B ve
C noktalarının oluşturduğu üçgen ile benzerdir. ABC üçgeni ile abc üçgeninin
yönü aynıdır (A dan B ye sonra C ye giderken yapılan dönme saat yelkovanına
ters ise, hız veya ivme poligonunda a dan b ye sonra c ye giderken dönme
saat yelkovanı yönüne ters olacaktır).
Hız
ve ivme poligonunda oluşan abc üçgeni mekanizma uzvunda bulunan A,B ve
C noktalarının oluşturduğu üçgen ile benzerdir. ABC üçgeni ile abc üçgeninin
yönü aynıdır (A dan B ye sonra C ye giderken yapılan dönme saat yelkovanına
ters ise, hız veya ivme poligonunda a dan b ye sonra c ye giderken dönme
saat yelkovanı yönüne ters olacaktır).
Yukarıda belirtilmiş olan teorem "Mehmke Teoremi" veya "hız ve ivme görüntü prensibi" olarak adlandırılır. Bu teoremin kullanım yeri bir cisim üzerinde iki noktanın hız ve ivmesini biliniyor ise, üçüncü bir noktanın hız ve ivmesinin bu üçgen benzerliğinden belirlenmesidir.