1.3 Temel Kavramlar-2
Serbestlik Dereceleri
Bir önceki sayfada değinilen sınıflandırmalar bazı açılardan (örneğin kuvvet iletimi) önemli ise de, kinematik çiftlerin en önemli özelliği olan hareket ile ilgilenmemektedir. Bir kinematik çift ile bağlanmış olan iki rijit cismin birbirlerine göre, kinematik çiftin özelliklerine bağlı olarak, farklı bağıl hareketleri olacaktır. Oluşan bu bağıl hareket bir kinematik çiftin en önemli özelliklerini verir. Bu bağıl hareket kıstasına göre sınıflandırmak için, serbestlik derecesi kavramına ihtiyaç vardır.
Uzay serbestlik derecesi, o uzayda bulunan bir cismin konumunu belirlemek için gerekli olan bağımsız parametre sayısıdır.
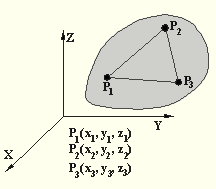Üç boyutlu bir uzayda -ki bu yaşadığımız genel uzay konumudur- bir cismin konumunu belirleyelim (Alttaki şekilde üç boyutlu koordinat ekseni ve cismin konumu gösterilmiştir).Cismin konumunu bu genel uzayda belirlemenin bir yolu, cismin üzerinde aynı doğru üzerinde bulunmayan her hangi üç noktanın (P1, P2, P3 ) konumunu belirlemektir. Bu üç noktanın konumu bilindikten sonra, rijidite kavramından dolayı bir başka noktanın bu noktalardan uzaklığı değişmeyeceğinden, diğer noktaların konumu belirlenmiş olacaktır. Bu üç noktanın her birinin konumu üç parametre ile belirlenir (P1(x1, y1, z1), P2 (x2, y2, z2) ve P3 (x3, y3, z3)). Bu durumda üç noktanın ve dolayısı ile cismin konumunu belirlemek için dokuz parametre gerekli görülür ise de, cismi rijit kabul ettiğimizden bu üç nokta arasında uzaklıklar sabit olacaktır. Bu sabit uzaklık şartı dokuz parametre arasındaki şu üç ilişkiyi tanımlayacaktır:
(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2 = a12
(x3 − x1)2 + (y3 − y1)2 + (z3 − z1)2 = a22
(x3 − x2)2 + (y3 − y2)2 + (z3 − z2)2 = a32
Dokuz parametre (xi, yi, zi : i = 1, 2, 3) ve bu parametreler arasında üç denklem bulunmaktadır. Bu durumda bu parametreler arasından sadece altısını tanımladığımızda üç noktanın ve dolayısı ile cismin konumu belirlenmiş olacaktır. Bağımsız parametre sayısı altı olduğundan genel uzayda serbestlik derecesi altıdır.
Soru: Gerekli olan bu altı parametreyi tanımlamakta herhangi bir kısıtlama var mıdır?
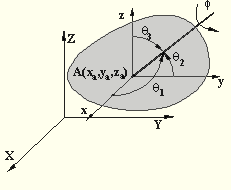Cismin konumunu belirlemek için mutlaka üç nokta gerekmez. Farklı bir tanım için alttaki şekilde görüldüğü gibi cisim üzerinde bir nokta ve bir doğru ele alalım. Cismin konumunu belirlemek için ilk olarak A noktasının konumunu üç parametre ile tanımlayabiliriz. Cisim üzerinde bulunan doğrunun yönünü belirlemek için, doğru ile X,Y ve Z eksenleri arasında kalan açıları kullanalım (θ1, θ2 ve θ3). Nokta ve doğru belirlendikten sonra cisim sadece doğru etrafında serbestçe dönebilir. Bu dönmeyi de bir açı ile belirlersek cismin konumu belirlenmiş olacaktır ve bu durumda yedi parametre kullanılmıştır (xa, ya, za, θ1, θ2, θ3 ve ϕ). Ancak doğru ile eksenler arasında kalan üç açı arasında:
cos2(θ1) + cos2(θ2) + cos2(θ3) = 1
bağlantısı vardır. Bu durumda cismin konumunu belirlemek için yine altı bağımsız parametre gereklidir (xa, ya, za, ϕ ve θ1, θ2, θ3 açılarından her hangi ikisi). Görüldüğü gibi, cismin konumunu belirlemek için farklı yaklaşımlar kullanılabilir ise de, gerekli olan bağımsız parametre sayısı daima sabittir.
Düzlemsel Uzayda Serbestlik Derecesi:
Düzlemsel bir uzay düşündüğümüzde, bir cismin bir düzlem içinde hareketi söz konusu olacaktır. Bu durumda cisim sadece iki yönde öteleyecek ve öteleme düzlemine dik bir eksen etrafında dönebilecektir. Öyle ise düzlemsel uzayda gerekli olan bağımsız parametre sayısı üçtür ve düzlemsel uzay serbestlik derecesi üç olacaktır. Bu serbestlik derecelerinin tanımı için aşağıdaki şekilde gösterildiği gibi, değişik parametreler kullanılabilir.
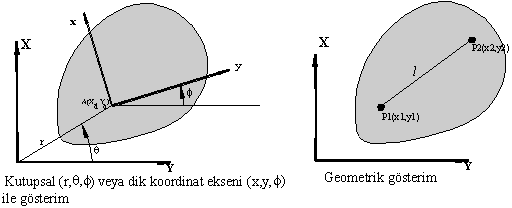
Yukarıda gösterilmiş olan genel ve düzlemsel uzaydan başka küresel ve iki boyutlu uzaylarda bulunmaktadır. Bu uzaylara ileride değinilecektir. Pratikte kullanılan mekanizmaların çalıştığı ortamlar çoğunlukla düzlemseldir.
Bir kinematik çiftin (mafsalın) serbestlik derecesi, o mafsalla birleştirilen cisimlerin birbirlerine göre bağıl konumlarını belirlemek için kullanılması gerekli bağımsız parametre sayısıdır. Kinematik çiftlerin serbestlik dereceleri ve bu serbestliklerin müsaade ettiği hareketin yönü ve tipi (dönme veya öteleme), kinematik çiftleri birbirinden ayıran en önemli özelliktir ve bu özellikler kinematik çiftlerin tiplerini belirlemekte kullanılır. Tablo I ve Tablo II ‘de bu özelliklere göre sınıflandırılan mafsallar görülmektedir.
En genel uzayın serbestlik derecesi 6 olduğundan ve bir kinematik çiftin bu serbestliklerden en az birini sınırlaması gerektiğinden, serbestlik derecesi en yüksek mafsalda 5 serbestlik bulunmalıdır (Tablo I). Ötelemeyi sınırlamadan dönme hareketlerini sınırlamak mümkün değildir ve bu nedenle 5 serbestlik dereceli kinematik çiftte bir öteleme hareketi sınırlandırılır.
Bu kinematik çiftleri teker teker inceleyin ve pratikte gördüğünüz kinematik çiftleri adlandırın.
Önemli olan, bir kinematik çiftin şekli değil, serbestlik derecesi ve bu serbestlik çeşidinin tipidir (Tablo I ve Tablo II′yi inceleyiniz).
