Örnek: Altı Uzuvlu Bir Mekanizmadaki Devreler
Şekil 1-A da 6 uzuvlu bir mekanizma görülmektedir. Mekanizmada hiç bir kapalı devre kalmaması için bu sefer iki mafsalın sökülmesi gereklidir. Sökülmesi gereken mafsal kişiden kişiye farklı olabilir. Ancak devre kalmayacak şekilde sökülmesi gereken minimum mafsal sayısı bir mekanizma için sabittir. Ayrıca mafsallar sökülür iken uzuvların zincirden ayrılmaması gereklidir. C ve B noktalarında bulunan mafsallar söküldüğünde (Şekil 1-B), mekanizmada devre bırakılmamış, açık zincirler oluşturulmuştur (istenir ise D ve E veya D ve A gibi iki farklı mafsal sökülebilir. Ancak örneğin B ve D mafsalı sökülemez, çünkü bu durumda bir uzuv zincirden koparılmış olur). C noktasının konumunu 1, 2, 3 ve 1, 5, 4 uzuvlarından oluşan açık kinematik zincirleri kullanarak yazmak istediğimizde (B mafsalı sökülmüş durumda), gerekli konum parametreleri tanımlayarak elde ettiğimiz vektör devre denklemi:
AoA + AC = AoDo + DoE + EC
olur. Karmaşık sayılarla vektör devre denklemi yazıldığında:
a2eiθ12 + a3eiθ13 = a1 + a5eiθ15 + a4eiθ14
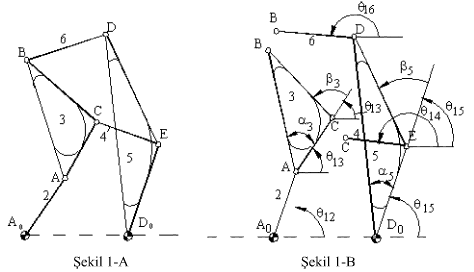
(a1 = |AoDo|, a2 = |AoA|, a3 = |AC|, b1 = |AB|, c3 = |CB|, a4 = |EC|, a5 = |DoE|, b5 = |DoD|, c5 = |ED|, a6 = |BD|)
B noktasının konumu vektörü, benzer bir şekilde 1, 2, 3 ve 1, 5, 6 uzuvlarından oluşan açık zincirleri kullanarak (C mafsalı açık olduğu varsayılarak), yazıldığında elde edilen vektör devre denklemi ise
A0A + AB = A0D0 + D0D + DB
olacaktır. Karmaşık sayılar kullanılarak yazıldığında:
a2eiθ12 + b3ei(θ13 + α3) = a1 + b5ei(θ15 + α5) + a6eiθ16
Dikkat edilir ise, 3 ve 5 uzuvlarının konumları birinci ve ikinci denklemlerde farklı vektörlerle belirlenmektedir ( 3 uzvu için AC ve AB vektörleri, 5 uzvu için D0E ve D0D vektörleri). Ancak bu vektörlerin şiddetleri yine uzuv boyutları olup aynı uzuv üzerinde bulunan iki vektörün birbirleri arasında sabit bir açı (α3 ve α5) bulunmaktadır. Bu açılar o uzuvların boyutları ile tanımlıdır. Bu nedenle her bir uzuv için sadece bir açısal konum parametresi (θ13 ve θ15) tanımlanmıştır.
Yazmış olduğumuz iki devre kapalılık denkleminde beş konum değişkeni bulunmaktadır (θ12, θ13, θ14, θ15 ve θ16). Bu konum değişkenlerinden birisi bağımsız değişken olarak belirlenir ise, iki vektör devre denkleminden kalan diğer dört değişkenin değeri bulunabilir.
Eğer B mafsalının bağlanmasını C mafsalı bağlandıktan sonra yapar isek bu durumda B mafsalı ile kapatacağımız devre ECBDE devresi olacaktır (4-3 ve 5-6 açık zincirleri) (önceki durumda B mafsalı açık olduğundan B mafsalı ile A0ABDD0A0 devresi oluşmuştu). Bu yeni durumda bu yeni devre için devre kapalılık denklemi
EC + CB = ED + DB
olacaktır. Karmaşık sayılar ile bu denklem:
a4eiθ14 + c3ei(θ13 + β3) = c5ei(θ15 + β5) + a6eiθ16
yazılabilir. Her her üç devre kapalılık denklemi ele alınır ise, elde edilen skaler denklem sayısı bilinmeyen parametre sayısından fazla olacaktır. Bu denklemleri için çözüm ancak bilinmeyen parametre sayısı kadar bağımsız skaler denklem olması ile mümkündür. Nitekim bu örnek için elde edilmiş olan birinci ve üçüncü vektör devre denklemlerini taraf tarafa topladığımızda:
A0A + AC + EC + CB = D0E + EC + ED + DB
denklemi çıkacaktır. Her iki tarafta bulunan EC vektörü gider. Şekil 2 de görüldüğü gibi aynı uzuv üzerinde bulunan üç vektör uzvun θ ile belirlenen konumuna bağımlı kalmaksızın aralarında sabit bir ilişkiyi korurlar. A, B, C noktaları aynı uzuv üzerinde olduğunda:
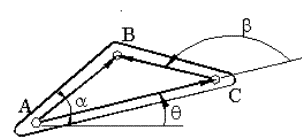
Aynı uzuv üzerinde bulunan ABC Noktaları
b = |AB| , a = |AC|, c = |CB|
AB = bei(θ + α) , AC = aeiθ , CB = cei(θ + β)
AC + CB = AB (Daima sağlanacak olan vektör denklemi)
Karmaşık sayılar ile yazdığımızda:
aeiθ + cei(θ + β) = (a + ceiβ)eiθ = bei(θ + α) = beiαeiθ
⇒ a + ceiβ = beiα
Dikkat edilirse, denklemde değişken açı olan ve uzvun konumunu belirleyen θ açısı değeri ne olursa olsun denklem sağlanmaktadır.
Öyle ise bu değerlendirme, örneğimizde 3 uzvu için AC + CB = AB ve 5 uzvu için D0E + ED = D0D sonucunu verecektir. Böylece birinci ve üçüncü vektör devre denklemleri toplandığında ikinci vektör devre denklemi elde edilmiştir. Öyle ise bu üç vektör devre denkleminden birisi diğer iki denkleme bağımlıdır. Bu nedenle elde edilmiş olan üç devre denkleminden sadece ikisi konum değişkenlerinin çözümü için kullanılabilir.
A0A + AC + CE = A0D0 + D0E
A0A + AB + BD = A0D0 + D0D
a2eiθ12 + a3eiθ13 + a4eiθ14 = a1 + a5eiθ15
a2eiθ12 + b3ei(θ13 + α3) + a6eiθ16 = a1 + b5ei(θ15 + α5)
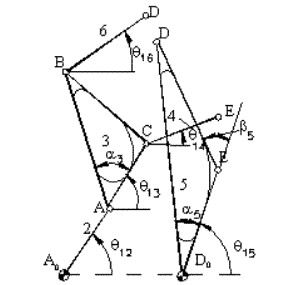
A ve E gibi farklı mafsallar sökülmüş kabul edilebilir (ve sonra birleştirilerek devre denklemi elde edilir). Mafsallar sökülürken hiçbir uzvun zincirden kopmadığına (en az bir mafsal ile bir başka uzva bağlı olduğuna) dikkat edilmelidir. Farklı mafsallar söküldüğünde farklı parametreler tanımlanabilir. Ancak her şartta denklem sayısı ve konum parametresi sayısı bir mekanizma için sabit kalacaktır. Farklı tanımlar kullanıldığında konum parametreleri arasında sabit açı farkları oluşabilir. Bu örnekte B ve C mafsalları yerine D ve E mafsalları söküldüğünde θ14 ve θ16 açı tanımları π kadar fark etmiştir.