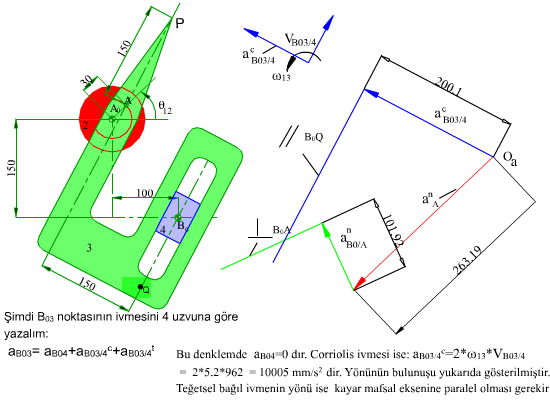
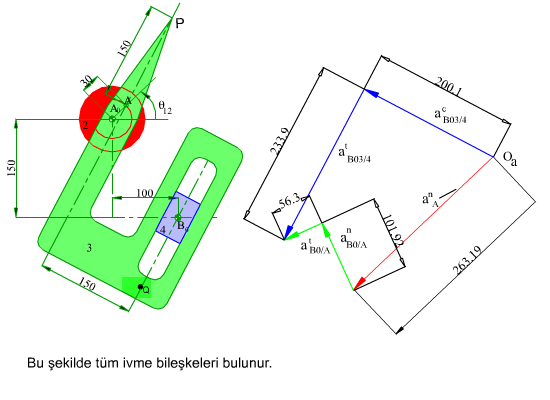
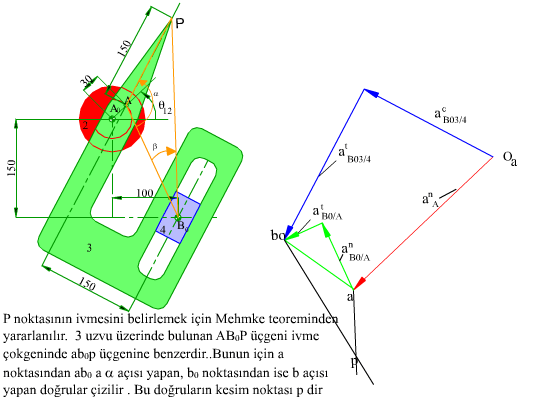
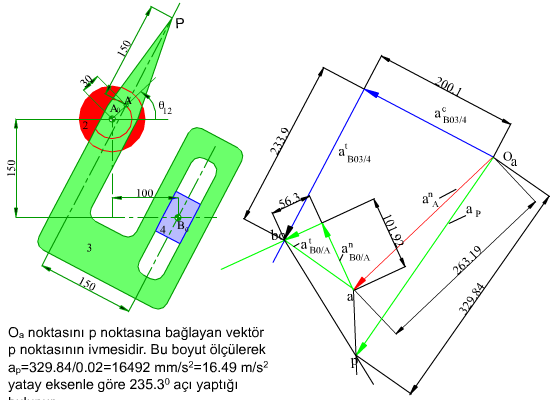
4.2 Mekanizmalarda Hız ve İvme Analizi -5

Örnek:

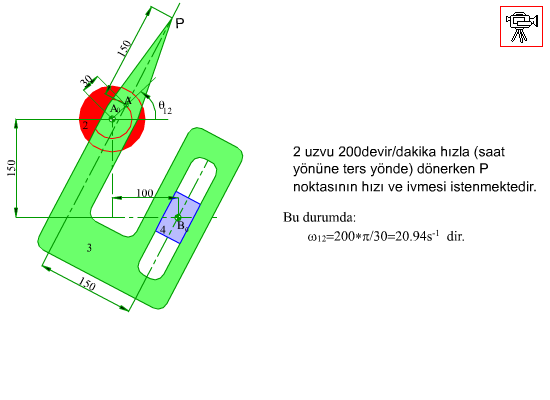
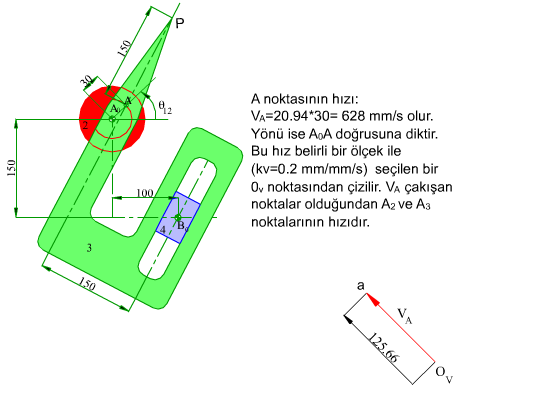
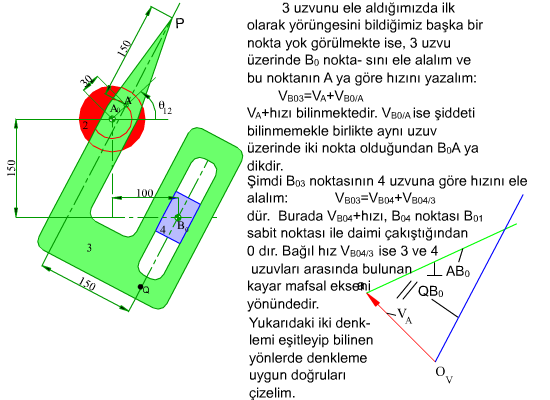
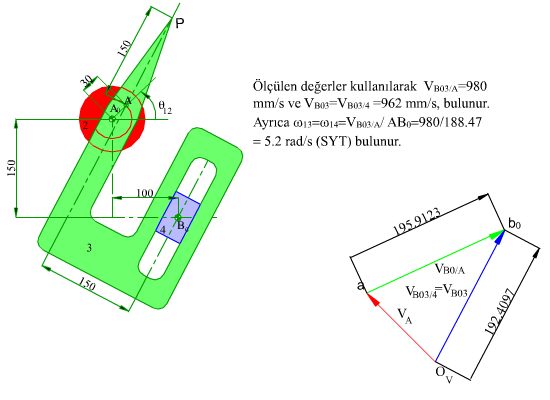
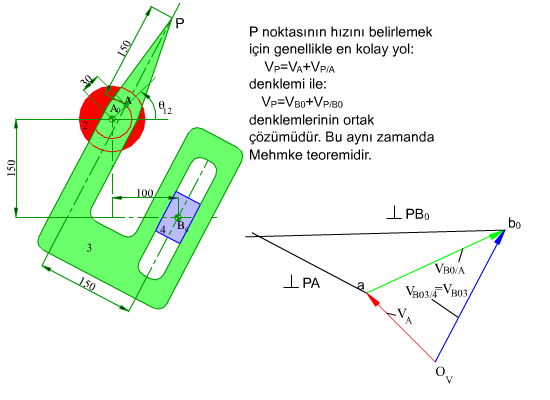
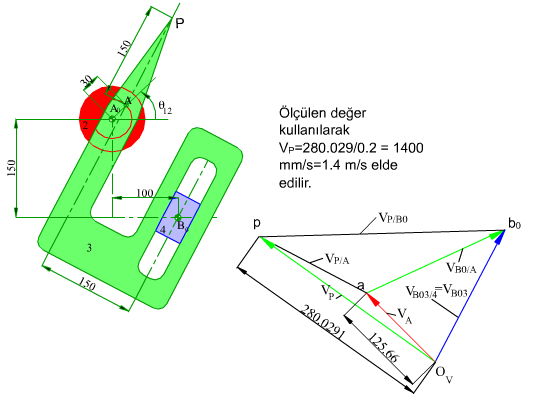
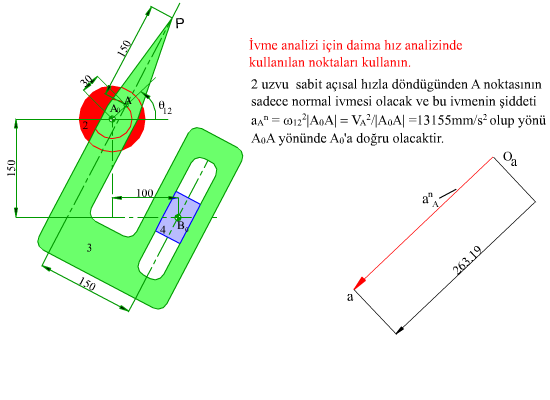
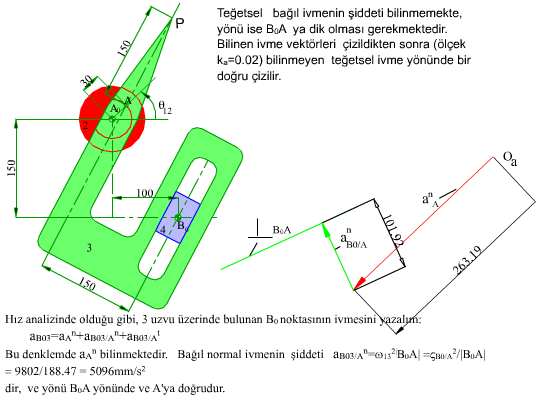
Yukarıda işleyişi gösterilen mekanizmanın A₀A kolu 200 devir/dakika sabit hızla dönerken P noktasının hız ve ivmesini bulalım.

Şimdi, aynı mekanizmayı analitik yöntemle çözelim.

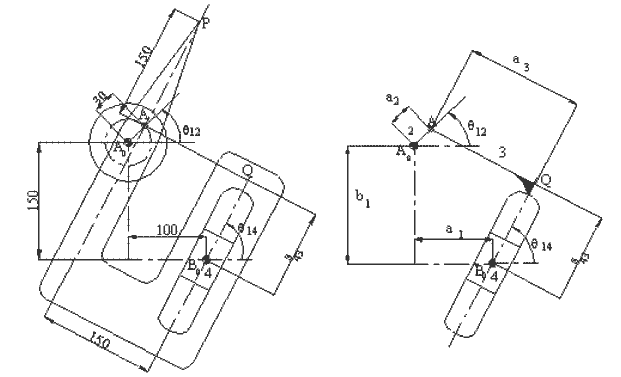
Uzuv boyutları: a₁ = 100, b₁ = 150, a₂ = 20, a₃ = 150 ve b₃ = 150 mm

Analitik yöntem kullanıldığında, devrenin belirlenmesi ve değişkenlerin tanımı temel sorundur. Mekanizmayı yukarıda sağda görüldüğü gibi çizmemiz durumunda, konum değişkenlerinin tanımlanması daha kolay olabilir. En önemli kural mekanizmada uzuv şekillerinin kafamızı karıştırmasına müsaade etmemeli, mafsalları ve onların müsaade ettikleri hareketleri inceleyerek hareket yönlerinde konum değişkenlerini tanımlamamızdır. Bu durumda mekanizma için devre kapalılık denklemini karmaşık sayılarla:

a₂e^iθ₁₂ = a₁ − ib₁ + s₄₃e^iθ₁₄ + ia₃e^iθ₁₄

yazabiliriz. Önceki kısımlarda açıklandığı gibi, bilinmeyen bağımlı konum değişkenleri (θ₁₄ ve s₃₄) için verilen bağımsız parametre değerine (θ₁₂) göre çözüm yapmamız gerekmektedir. Ayrıca devre kapalılık denkleminin birinci ve ikinci türevi alınarak hız ve ivme devre denklemleri elde edilebilecektir. Bu denklemlerde θ₁₄ ve s₃₄ parametrelerinin birinci ve ikinci türevleri bilinmeyen hız ve ivme parametreleri olacaktır.

Devre kapalılık denklemini çözmek için θ₁₄ parametresini içeren terimleri bir tarafta toplar isek:

(s₄₃ + ia₃)e^iθ₁₄ = a₂e^iθ₁₂ − a₁ + ib₁

ve karmaşık eşleniği:

(s₄₃ − ia₃)e^−iθ₁₄ = a₂e^−iθ₁₂ − a₁ − ib₁

olacaktır. Bu iki deklemi taraf tarafa çarpıp s₄₃ için çözüm yaptığımızda:

s₄₃ = \displaystyle \sqrt{{{{\text{a}}_{1}}^{2}+{{\text{b}}_{1}}^{2}+{{\text{a}}_{2}}^{2}-{{\text{a}}_{3}}^{2}-2{{\text{a}}_{1}}{{\text{a}}_{2}}\cos {{\text{θ}}_{{12}}}+2{{\text{b}}_{1}}{{\text{a}}_{2}}\sin {{\text{θ}}_{{12}}}}}

olarak elde edilir. s₄₃ çözümü elde edildikten sonra θ₁₄ açısı:

e^iθ₁₄ = \displaystyle \frac{{{{\text{a}}_{2}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}}}}-{{\text{a}}_{1}}+\text{i}{{\text{b}}_{1}}}}{{{{\text{s}}_{{43}}}+\text{i}{{\text{a}}_{3}}}}

denkleminden elde edilebilir (reel sayılar ile θ₁₄ açısının bu denklemden elde edilmesi okuyucuya bırakılmıştır). P noktasının konum vektörü A₀P ise:

A₀P = a₂e^iθ₁₂ + b₃e^iθ₁₄

dir. Yörünge şekilde gösterilmektedir.

Yukarıda verilmiş olan yöntemden farklı olarak, istenir ise, ilk olarak A₀AB₀ ve AQB₀ üçgenleri kullanılarak üçgen çözümü ile mekanizmada bilinmeyen konum parametrelerinin değerleri bulunabilir. Bu yöntem okuyucuya bırakılmıştır.

Hız analizi için devre denkleminin türevi alınıp v₄₃ = \displaystyle {\dot{\text{s}}} ₄₃ ve ω₁₄ = \displaystyle {\dot{θ}} ₁₄ hız değişkenlerine çözüm yapılabilir. Sonuç denklemler:

v₄₃ = [(a₃/s₄₃)cos(θ₁₂ − θ₁₄) − sin(θ₁₂ − θ₁₄)]ω₁₂

ω₁₄ = (a₂/s₄₃)cos(θ₁₂ − θ₁₄)ω₁₂

Benzer bir şekilde, hız devre denkleminin türevi alındığında (ω₁₂ sabit kabul edilmiştir) ve hız değişkenlerine (a₄₃ = \displaystyle {\ddot{\text{s}}} ₄₃ ve α₁₄ = \displaystyle {\ddot{\theta }} ₁₄):

a₄₃ = −(a₂/s₄₃²)ω₁₂[(ω₁₂ − ω₁₄)(a₃s₄₃sin(θ₁₂ − θ₁₄) + s₄₃²cos(θ₁₂ − θ₁₄)) + a₃v₄₃cos(θ₁₂ − θ₁₄)]

α₁₄ = −(a₂/s₄₃²)ω₁₂[(ω₁₂ − ω₁₄)s₄₃sin(θ₁₂ − θ₁₄) + v₄₃cos(θ₁₂ − θ₁₄)]

Hız ve ivme parametreleri bulunduktan sonra P noktasının hız ve ivmesi bu değerlere göre bulunabilir:

v_P = ia₂ω₁₂e^iθ₁₂ + ib₃ω₁₄e^iθ₁₄

a_P = −a₂ω₁₂²e^iθ₁₂ + ib₃α₁₄e^iθ₁₄ − b₃ω₁₄²e^iθ₁₄

Bir tam devirde P noktasının Hız ve ivmesinin değişimi kutupsal koordinatlarda aşağıdaki şekillerde gösterilmiştir.

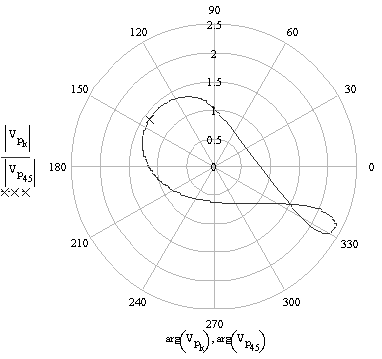
P noktası hızının kutupsal gösterimi

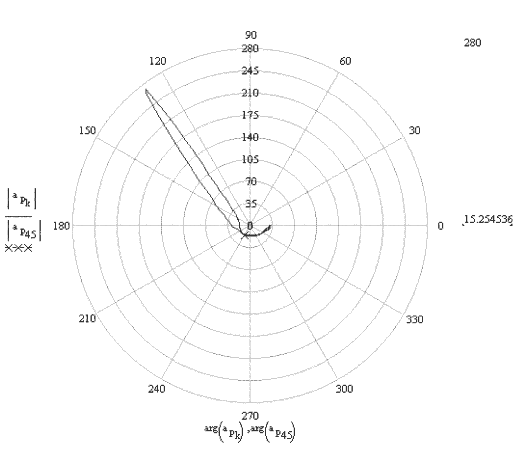
P noktası ivmesinin kutupsal gösterimi

Aynı problemin Geogebra ile de konum analizi yapılmış olup aşağıdaki videoda anlatılmıştır.