Ek-2
Basit Mekanizmalar İçin Bilgisayar Programları
Uygulamalarda basit dört uzuvlu mekanizmalar veya bu basit dört uzuvlu mekanizmalardan seri bağlanarak elde edilen mekanizmalar çok sık rastlanmaktadır. Bu mekanizmalar için hazırlanacak ufak fonksiyon programları gerek Excel paket programı içinde Macro programlar olarak ve gerek VisualBasic lisanı kullanılarak yazılan genel veya özel amaçlı mekanizma programları için çok önemli yapı taşlarını oluşturmaktadır.
2.1. Kartezyen koordinatları verilen bir vektörün uzunluğu ve yön açısını bulmak:
x ve y değerleri verildiğinde OP uzunluğu (r = Boy(x,y)) ve OP doğrusunun pozitif x ekseni ile yaptığı açıyı radyan olarak (θ = Açı(x,y)) verecek iki basit fonksiyon programıdır. Dikkat edilir ise, açı(x,y) programı basic lisanında var olan Atn(x) fonksiyonunu kullanmaktadır. Ancak açının hangi bölgede olduğunu x ve y bileşenlerinin işaretlerinden bularak Atn(x) fonksiyonundan farklı olarak verilen x ve y değerine göre var olan tek doğru çözümü kullanıcıya vermektedir. Fonksiyonların dışında PI ve Eps sabit değerleri tanımlanmıştır. x < Eps olduğunda x = 0 kabul edilerek y nin işaretine göre açı 900 veya -900 kabul edilmiştir (bu tür bir önlem alınmaz ise küçük x değerlerinde sıfıra bölme hatası ile karşılaşılır).
Global Const PI = 3.1415926
Global Const Eps = 0.0000001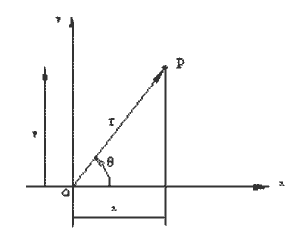
Function Boy(X, Y)
Boy = Sqr(X ^ 2 + Y ^ 2)
End Function
Function Açı(X, Y)
Dim AA
If Abs(X) > Eps Then
AA = Atn(Y / X)
If X < 0 Then
AA = AA + PI
Else:
If Y < 0 Then AA = AA + 2*PI
End If
Else:
If Y > 0 Then AA = PI / 2 Else AA = -PI / 2
End If
Açı = AA
End Function
2.2. Ters Sinüs ve Kosinüs fonksiyonları:
Normal olarak Pascal ve Basic lisanlarında Atn(x) – ters tanjant fonksiyonu dışında ters trigonometrik fonksiyon yoktur. Mekanizma analizi sırasında ters sinüs (Asin(X)) ve ters kosinüs (Acos(X)) fonksiyonlarına ihtiyaç olmaktadır. Dikkat edilir ise, bu fonksiyonlar ACOS un ve ASIN in değerlerinden sadece birini vermektedir. Kullanıcı eğer diğer çözümü istiyor ise, bu açıya 180 derece eklemeli veya çıkarmalıdır.
Function Acos(X)
Acos = Atn(-X / Sqr(-X * X + 1)) + 2 * Atn(1)
End Function
Function Asin(X)
Asin = Atn(X / Sqr(-X * X + 1))
End Function
2.3. Üçgen Çözümü:
Mekanizmaların analizi sırasında üç kenarı verilen bir üçgenin bir açısını (Açı3 = AçıCos(U1,U2,U3)) veya iki kenarı ve açısı verildiğinde karşı kenar uzunluğunu (U3 = BoyCos(U1,U2;Açı3)) bulmak için hazırlanmış fonksiyon programlarıdır.
Function AçıCos(u1, u2, u3)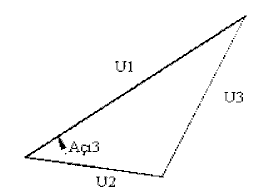
Dim u u = (u1 * u1 + u2 * u2 – u3 * u3) / (2 * u1 * u2)
AA = Acos(u)
AçıCos = AA
End Function
Function BoyCos(U1, U2, Açı3)
BoyCos = (U1 ^ 2 + U2 ^ 2 – 2 * U1 * U2 * Cos(Açı3)) / (2 * U1 * U2)
End Function
2.4. Basit Mekanizmaların Analizi:
2.4-a) Dört-Çubuk Mekanizması
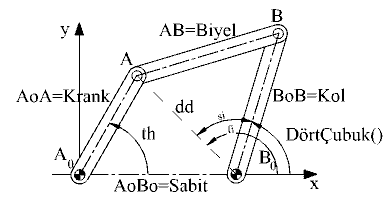
Bu fonksiyon programı uzuv boyutları, giriş kolu açısı ve bağlantı şekli verilen bir dört-çubuk mekanizmasının çıkış kolu açısını bulmak için yazılmıştır. Kullanıcı s sayısını +1 veya -1 tanımlayarak mekanizmanın açık veya çapraz bağlandığını belirleyecektir.
Program incelenir ise, önceden yazılmış olan Boy(), Açı() ve AçıCos() fonksiyonları bu fonksiyonda kullanılmıştır. Bu fonksiyonun kullanılabilmesi için diğer fonksiyonlarında programda yazılı olması gerekir. Programa basit ekler yaparak biyel açısını ve bağlama açısını bulmak için fonksiyonlara çevirmek mümkündür.
Function DörtÇubuk(Krank, Biyel, Kol, Sabit, s, th)
Dim dd, fi, si As Double
Dim xd, yd As Double
xd = -Sabit + Krank * Cos(th)
yd = Krank* Sin(th)
dd = Boy(xd, yd)
fi = Açı(xd, yd)
si = AçıCos(Biyel, dd, Kol)
DörtÇubuk = fi – s * si
End Function
2.4-b) Krank-Biyel Mekanizması:
Bu fonksiyon programı uzuv boyutları, giriş kolu açısı ve bağlantı şekli verilen bir krank-biyel mekanizmasının çıkış kolu öteleme uzaklığını bulmak için yazılmıştır.
Kullanıcının s sayısını +1 veya −1 tanımlayarak pistonun şekilde görüldüğü gibi krank eksenine göre pozitif x ekseni yönünde (s = +1)veya ters yönde (s = −1) olduğunu belirlemesi gerekir. Program önceden yazılmış olan Asin() fonksiyonunu kullanmaktadır.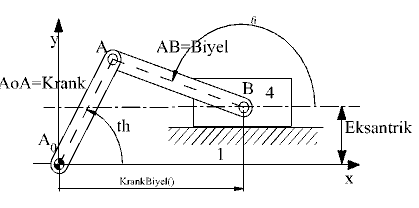
Function KrankBiyel(Krank, Biyel, Eksantrik, s, th)
Dim fi As Double
fi = Asin((Krank* Sin(th) – Sabit) / Eksantrik)
If s = 1 Then fi = 4 * Atn(1) – fi
KrankBiyel = Krank * Cos(th) – Biyel * Cos(fi)
End Function
2.4-c) Kol-Kızak Mekanizması:
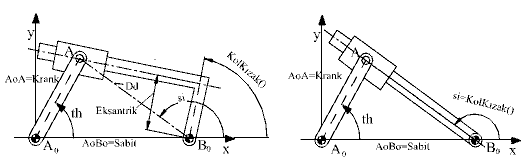
Kol-kızak mekanizmasının santrik veya eksantrik olması a3 değerinin sıfır olup olmaması ile ilgilidir. Eksantrikliklik olduğunda çıkış kolu iki değişik şekilde monte edilebileceğinden s değeri +1 (şekilde gösterilen durum) veya -1 olarak girilmelidir (Santrik için s her hangi bir değer olabilir).
Function KolKızak(Krank, Sabit, Eksantrik, s,th)
Dim Xd,Yd as double
Xd = Krank * Cos(th) – Sabit
Yd = Krank * Sin(th)
Si= Açı(Xd,Yd)
If Eksantrik=0 then
Fi=Si
Else
Dd=Boy(Xd,Yd)
Fi=si-s*Asin(Eksantrik/Dd)
End If
KolKızak = Fi
End Function
Yukarıda yazılmış olan fonksiyon programları Excel paket programı içinde, kullanıcı tarafından tanımlanmış fonksiyon olarak tıpki diğer Excel fonksiyonları gibi kullanılabilir. Ayrıca, yukarıda yazılmış olan programların Excelde birleştirilerek de kullanılması mümkündür. Ayrıca bu programların VisualBasic içinde de kullanılması mümkündür. VisualBasic platformunun grafik özellikleri ile birlikte kullanıcı animasyon yapabilecek programlarda hazırlayabilir.
Örnek 1:
Yukarıda hazırlanmış olan programlar ile çok sayıda değişik mekanizmanın analizi kolayca yapılabilecektir. Aşağıda gösterilen mekanizmanın bir dört-çubuk ve bir krank-biyel mekanizmasının seri olarak bağlanması ile elde edildiği görülür ise, ilk olarak dört-çubuk mekanizması çıkış açısı (th4) DörtÇubuk() fonksiyonu kullanarak belirlenir. Th4-25° giriş açısı olarak KrankBiyel() fonksiyonu kullanılarak strok çözülebilir.
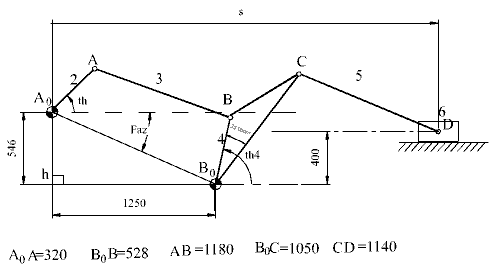
İlk olarak sabit uzuv boyutlarını (sabit açılar da dahil) Excel üzerinde yerleştirelim.
| A | B | C | D | E | |
| 1 | Dört-Çubuk | Krank-Biyel | |||
| 2 | Krank | 320 | Krank 2 | 1050 | |
| 3 | Biyel | 1180 | Biyel2 | 1140 | |
| 4 | ÇıkışKolu | 528 | Eksantrik | 400 | |
| 5 | SabitU_y | 1250 | AÇI 4 | 0.43633231 | 25 |
| 6 | SabitU_d | 546 | |||
| 7 | SabitUzuv | 1364.044 | |||
| 8 | SabitU Açı | 2.72977 | 156.40429 | ||
| 9 | Faz | 0.411823 | 23.595705 |
B8 hücresinde görülen açı radyan olarak B0A0 vektörünün yatay ile yaptığı açıdır (bu değeri ATAN2(-B5;B6) şeklinde ATAN2() Excel fonksiyonu kullanarak elde edebiliriz. Faz açısı ise bu açıyı tamlar açı olup B9 hücresine =pi()-B8 yazarak elde edilebilir. D5 hücresinde ise 4 uzvunda ∠BB0C açısı radyan olarak bulunmaktadır. B ve D kolonunda görülen hücrelere A kolonunda görülmekte olan isimler etiket adı olarak verilmiştir (örneğin B2 hücresi ismi Krank, D2 hücresi ismi ise Krank2 dir).
Sabit değerler girildikten sonra, A16-A40 hücrelerine 15º aralıklarla th krank açısı 0º ila 360º arasında girilmiştir.
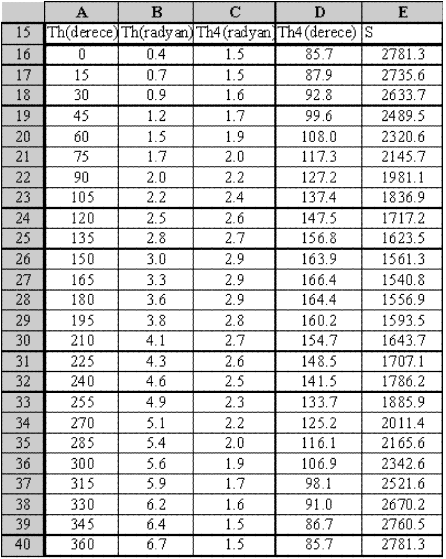
A kolonunda verilmekte olan açılar yatay ile krankın yaptığı açılardır. B kolonunda ise bu krank açısı radyana çevrildikten sonra sabit uzva göre açı olması için B9 hücresinde bulunan Faz açısı değeri çıkarılmıştır (isim vermedi iseniz B9 hücresini sabitlemek için $B$9 olarak girin). Şimdi C16 hücresine gelinir ve
“=DörtÇubuk(Krank;Biyel;ÇıkışKolu;SabitUzuv;1;B16)“
yazılır ise, th4 çıkış kolu açısı hesap edilir. Formülün C16-C40 hücrelerine kopya edilmesi ile tüm th açılarına göre Th4 açısı elde edilmiş olur. D kolonunda bu açı dereceye çevrilmiştir. Şimdi krank-biyel mekanizması için çözüm yapılabilir. Bunun için E16 hücresine
“=KrankBiyel(Krank2;Biyel2;Eksantrik;1;(C15-Açı4)) + SabitU_y“
komutunu yazalım. Bununla piston ötelemesini veren s parametresi değeri bulunacaktır. Denklemi E16-E40 hücrelerine kopyalar isek her 15° krank açısı için öteleme uzunluğunu belirlemiş oluruz. Sonucu grafik olarak Excel Chart komutu kullanarak göstermemiz mümkündür.
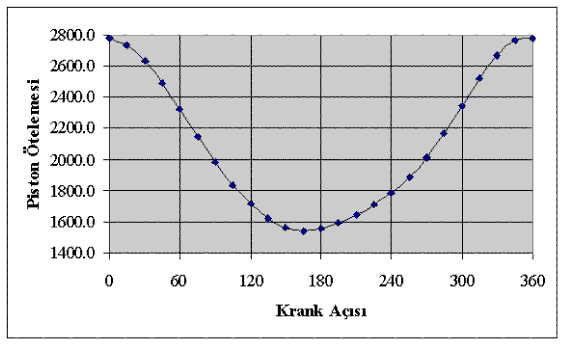
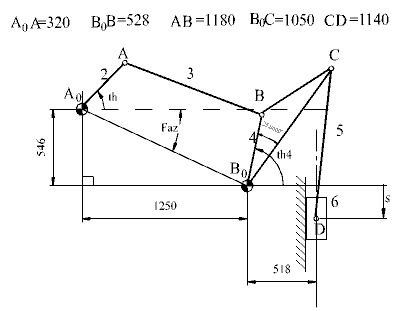Şekil a
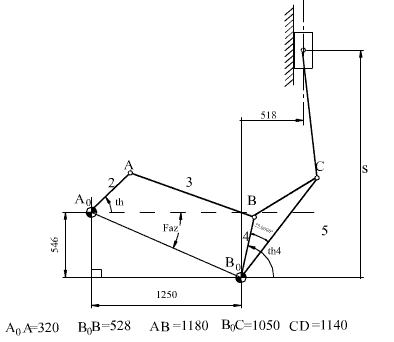Şekil b
Mekanizmayı oluşturan krank-biyel mekanizmasını yukarıdaki şekillerden biri gibi değiştirdiğimizde, dikkat edilir ise dört çubuk mekanizması ve dolayısı ile th4 aynı kalacaktır. Krank-Biyel mekanizmasında ise, giriş kolu açısını kayar çift eksenine paralel bir doğruya göre ölçmemiz gerekeceğinden giriş kolu açısı (th4 – ∠BB0C + pi/2) olmalıdır. Bu durumda Şekil a da E16 hücresine s değerini bulmak için E16 hücresine
“=KrankBiyel (Krank2 ;Biyel2 ;Eksantrik ;1;(C15-Açı4+PI()/2))“
komutunu tuşlayıp ve bu komutu E16-E40 hücrelerine kopyalamamız yeterlidir. Şekil b de görülen mekanizma için ise E16 hücresine
“= -KrankBiyel(Krank2 ;Biyel2 ;Eksantrik ;-1;(C15-Açı4+PI()/2)) “
komutunu tuşlamamız gerekecektir. Dikkat edilir ise her iki durumda pozitif x ekseni dikey aşağıya doğrudur. Ikinci durumda mekanizmanın şeklinden dolayı bağlantı durumunu gösteren s değeri −1 girilmiş ve fonksiyonun eksi değeri piston ötelemesi olarak alınmıştır. Sonuçta piston ötelemesi Şekil a için şekil c de ve şekil b için de şekil d de gösterildiği gibi elde edilmiştir. (Şekil d de görülen iki hörgüçlü hareketin nedenini değerlendirin).
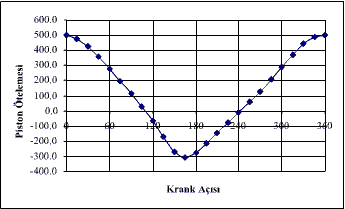Şekil c
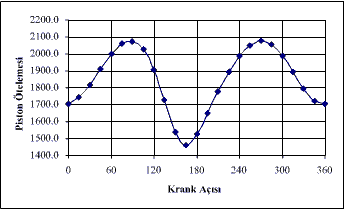Şekil d
Excel Kütüğü için tıklayınız: sixlink.xls.
