2.4 Grübler Denklemi

Genel serbestlik derecesi denklemi özel durumlar için daha basit hale getirilebilir. Bu şekilde özel durumlar için geçerli olan belirli bazı kuralların elde edilmesi mümkün olacaktır. İlk olarak ele alacağımız durum, uygulamada en sık rastlanılan: bir serbestlik dereceli (F = 1), düzlemsel (λ = 3) ve sadece döner veya kayar mafsal (f_i = 1, ∑f_i = j) kullanan mekanizmalar olacaktır. Bu değerler genel serbestlik derecesi denkleminde kullanıldığında:

3l − 2j − 4 = 0

(1)

Bu denkleme Grübler Denklemi diyeceğiz (Grübler denklemi genel serbestlik derecesi denkleminden önce bulunmuştur).

Grübler denklemini inceleyerek bu tip mekanizmalar ile ilgili çeşitli özellikleri belirleyebiliriz:

1. Grübler denklemini sağlayan mekanizmalarda uzuv sayısı çifttir.
   l ve j uzuv ve mafsal sayısını gösterdiğinden, tam sayı olmaları şarttır. Mafsal sayısı j ne olursa olsun 2j daima çift sayıdır. Aynı şekilde, (2j + 4) çift sayı olacaktır. 3l = 2j + 4 olduğundan, bu denklemin sağlanabilmesi 3l in çift sayı olması ile mümkündür. 3 ile çarpılan bir sayının sonuçta çift sayı olabilmesi sadece sayının çift sayı olması ile mümkündür. Bu durumda mekanizmada bulunan uzuv sayısı (l), çifttir.

Mekanizmada bulunan iki elemanlı uzuv sayısı dört veya dörtten fazla olmalıdır.
Kinematik eleman sayısı k olan uzuvların sayısı l_k olsun. Bir elemanlı uzuv olamayacaktır (l₁ = 0) çünkü uzuv tanımında, uzvun en az iki elemanlı olduğu belirtilmiştir. Toplam uzuv sayısı bu uzuv sayılarının toplamıdır:

l = l2 + l3 + l4 + l5 + … + ln

(2)

veya

3l = 3l2 + 3l3 + 3l4 + 3l5 + … + 3ln

(3)

(bu denklemlerde l₂ mekanizmada iki elemanlı uzuvların sayısını, l₃ üç elemanlı uzuvların sayısını, v.s. belirtmektedir). Mekanizmada bulunan kinematik eleman sayısı ise:

2l2 + 3l3 + 4l4 + … + nln = kinematik eleman sayısı

(4)

İki kinematik eleman bir kinematik çift oluşturduğuna göre, kinematik eleman sayısı mafsal sayısının iki katı olacaktır:

2j = 2l2 + 3l3 + 4l4 + … + nln

(5)

(3) ve (5) denklemlerini Grübler denklemine (1) yerleştirdiğimizde

l₂ − (l₄ + 2l₅ + 3l₆ + … + (n − 3)l_n) = 4

veya

l₂ = 4 + P

olur. Burada

P = l₄ + 2l₅ + 3l₆ + … + (n − 3)l_n

dir. Mekanizmada bulunan bir uzuvda kinematik eleman sayısı mekanizmada bulunan uzuv sayısının yarısından fazla olamaz. P daima pozitif bir değer alacaktır ve en küçük değeri, mekanizmada bulunan uzuvlar iki veya üç elemanlı ise, sıfırdır (uzuv sayısı değerleri eksi olamaz). Bu durumda iki elamanlı uzuvların sayısı P = 0 olduğunda l₂ = 4 tür. Bunun dışında durumlarda ise iki elemanlı uzuv sayısı mutlaka 4 ten fazla olacaktır.

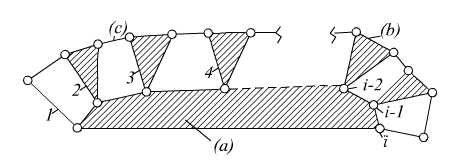
Yukarıdaki şekilde gösterildiği gibi, (a) gibi kinematik eleman sayısı maksimum olacak bir uzuv düşünelim. Maksimum eleman sayısı i olsun. Bu uzvun her bir elemanı bir kinematik çift oluşturacağından, i kadar (b) tipte uzuv (a) uzvuna bağlanacaktır. Mevcut uzuv sayısı (i + 1) olmuştur ancak henüz kapalı bir zincir yok-tur. Eklenecek bir uzuv (a) uzvunun kinematik eleman sayısını artırmaz. Öyle ise minimum sayıda (c) tipinde uzuv kullanarak kapalı bir zincir elde edilir ise, (a) uzvunda kinematik eleman sayısı maksimum olur. Bu düşünüldüğünde, (i − 1) kadar (c) tipinde uzuv kapalı zincir oluşturmak için yeterlidir. Bu mekanizmada uzuv sayısı:

l = 1 + i + (i − 1)

veya

i = l / 2

olur.