3.5 Vektör Devre Denklemlerinin Grafik Çözümü

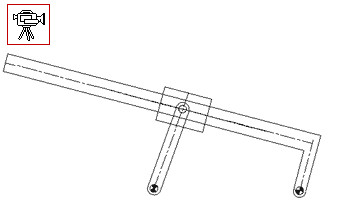
Bir mekanizmanın kinematik analizini yaparken mekanizmayı mümkün olan en basit şekilde çizmemiz yapacağımız işlerini kolaylaştırır. Bu nedenle uzuvlar bir çizgi ile gösterilebilir. Bu çizgilerin uçları bir sembolle gösterilmiş olduğundan, bu çizgiler gerçek anlamda vektördürler ve mutlaka bir ok şeklinde gösterilmelerine gerek yoktur. Yani genel olarak baktığımızda, mafsal merkezlerini (daima çakışan noktaları) değişik semboller (harfler) kullanarak işaretlediğimizde, elde ettiğimiz şekil, vektör devre denklemlerinin grafik gösterimidir. Bu nedenle devre kapalılık denklemleri yazılabilmiştir. Grafik çözüm için yapılması gereken, bu şeklin belirli bir ölçekle kağıt üzerine çizilmesidir (veya bir bilgisayar paket programı kullanarak bilgisayar ekranında benzer bir şekilde çizim yapılabilir. Bu durumda mekanizma ne kadar küçük veya ne kadar büyük olursa olsun görüntüyü ölçeklendirebildiğimizden gerçek boyutlar kullanılabilir).

Birisi sabit uzuv olmak üzere size dört çubuk verilir ve bunları bir zincir haline getirmeniz istenirse, çözüm tek değildir.

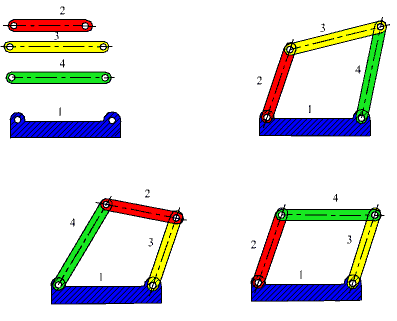
Görüldüğü gibi üç farklı mekanizma elde edilmiştir. Sabit uzva bağlı uzuvların sağ-sol yer değiştirmesi yeni bir mekanizma değildir (sadece aynı mekanizmanın ön veya arka görünüşü olur). Öyle ise bir mekanizmanın tanımlanmış olması için sadece uzuv boyutlarının bilinmesi yeterli değildir. Hangi uzvun hangi uzva hangi mafsalla bağlı olduğu da bilinmelidir.

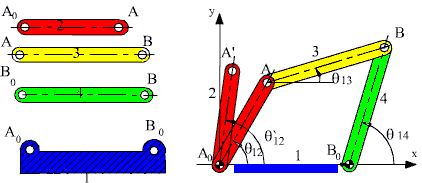
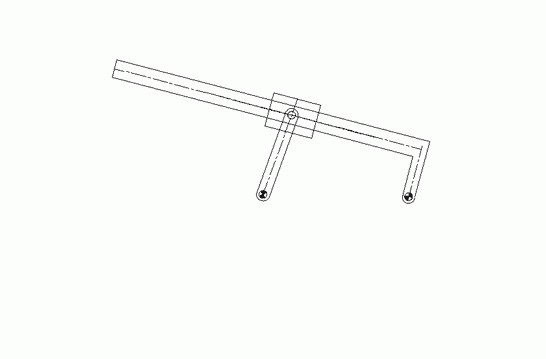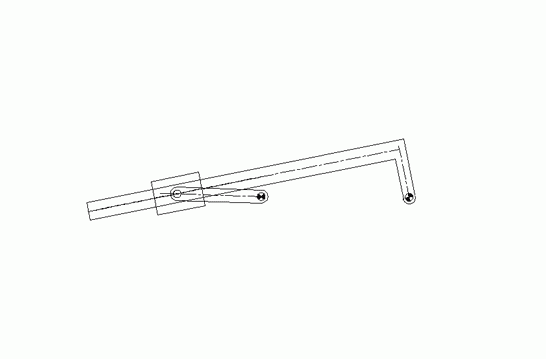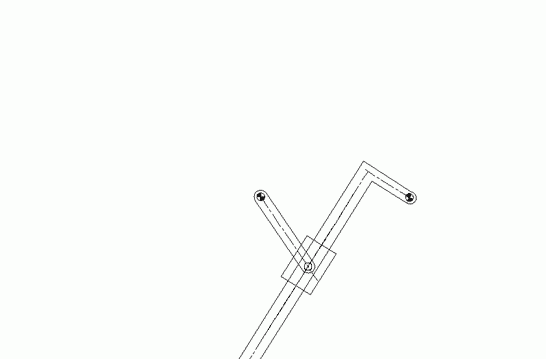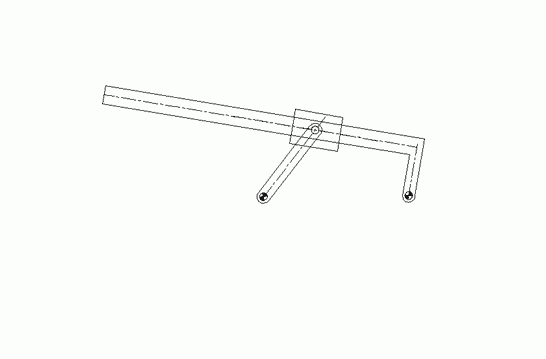
Mekanizmanın monte edilmiş bir konumu biliniyor ise, hareket sırasında uzuvların gelebileceği konumlar sınırlandırılmış ve mekanizmanın hareketi belirlenmiş olacaktır. Şimdi, bu mekanizmanın ekseni A₀ olan döner mafsalı (2 uzvunu) θ₁₂ açısından θ₁₂′ açısına getirdiğimizde diğer uzuvların konumunu bulalım.

A noktasının yeni konum vektörü (A₀A′) θ₁₂′ verildiğinde şiddet ve yönü bilinmektedir. Vektör devre denklemi:

A₀A + AB = A₀B₀ + B₀B

A noktası A’ (biliniyor) ve B noktası B’ (bilinmiyor) ile değiştirildiğinde, B noktası daima çakışan nokta olduğundan bu yeni konum için:

A₀A′+ AB′ = A₀B₀ + B₀B′

olacaktır. Bu denklem aynı zamanda:

A′B′ = A₀B₀ − A₀A′ + B₀B′

veya:

A′B′ = A′A₀ + A₀B₀ + B₀B′

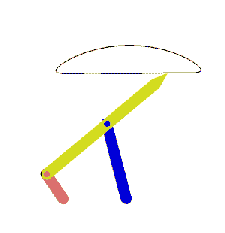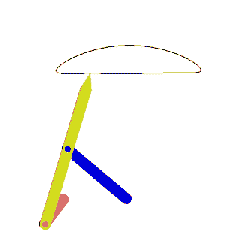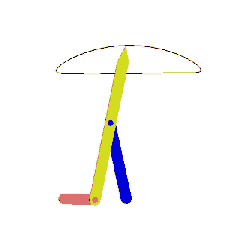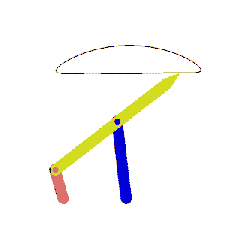
şeklinde yazılabilecektir. A′A₀ + A₀B₀ vektör toplamı A′B₀ vektörüdür. A′A₀ ve A₀B₀ vektörleri şiddet ve yön olarak bilinmektedir. A′B′ ve B₀B′ vektörlerinin boyutları bilinmektedir. Bu vektörlerin başlangıç noktaları olan A′ ve B₀ noktalarının konumu bilindiğine göre, B noktasının yeni konumu B′ nü belirlemek için A′ merkezli AB yarı çaplı bir yay ile B₀ merkezli B₀B yarı çaplı bir yay çizdiğimizde bu yayların kesiştikleri nokta B′ konumunu belirleyecektir.

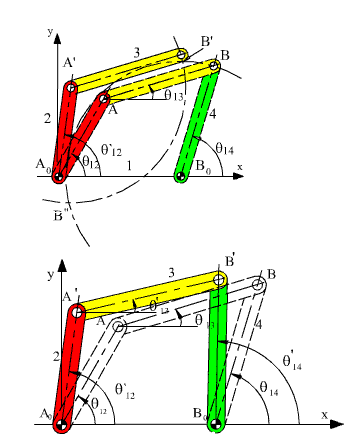
Bu iki yayın iki kesişme noktası (B′ ve B″) olacaktır. Ancak bu kesişme noktalarından birine mekanizma ilk verilmiş olan A₀ABB₀ konumundan geçebilmesi için mafsallardan birinin sökülüp bir uzuv hareket ettirildikten sonra yeniden bağlanması ile mümkün olacaktır. Eğer bu iki daire kesişmez ise, mekanizma verilmiş olan yeni θ₁₂′ açısı için monte edilmiş olarak bulunamaz.

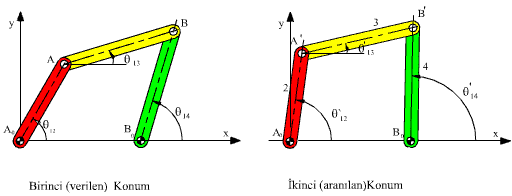
Başlangıçta, aynı uzuvlar yukarıda gösterildiği gibi monte edilmiş olarak verilse ve 2 uzvu θ₁₂ açısından θ₁₂′ açısına getirdiğimizde diğer uzuvların konumunu bulmak ister isek, bu sefer çözüm farklı olacaktır.

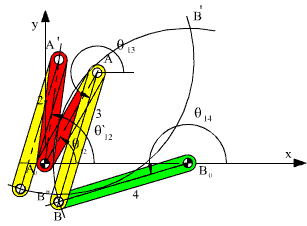
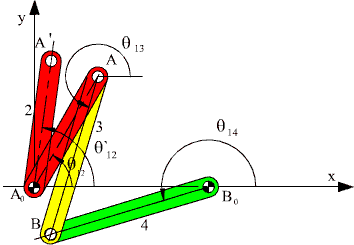
Görüldüğü gibi A′ den AB yarıçaplı daire ve B₀ dan B₀B yarıçaplı daireler B′ ve B″ noktalarında kesişir. Mekanizmanın verilen A₀ABB₀ konumundan A₀A′B′B₀ konumuna geçebilmesi için demonte edilmesi gerekecektir. Bu sefer verilen başlangıç konumuna göre çözüm A₀A′B″B₀ konumu olacaktır.

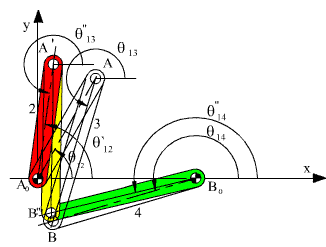
Bu yöntem iki kenarı ve kenarlar arasında kalan açısı verilen bir üçgenin üçüncü kenarının ve açılarının bulunması (AA₀B₀ üçgeni: A₀A ve A₀B₀ kenarı ile θ₁₂ açısı veriliyor, üçgenin bilinmeyen B₀A kenarı ve B₀A nın A₀B₀ ile yaptığı açı belirleniyor) ve ikinci olarak üç kenarı bilinen bir üçgenin (ABB₀ üçgeni: AB, BB₀ uzuv boyutları olduğundan ve AB₀ ilk üçgenin çözümü sonucu biliniyor) çiziminden farklı bir yöntem değildir.

Örnek:

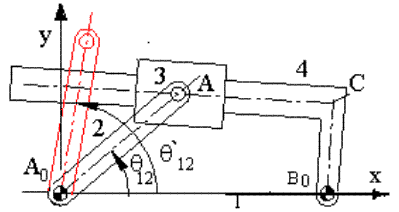
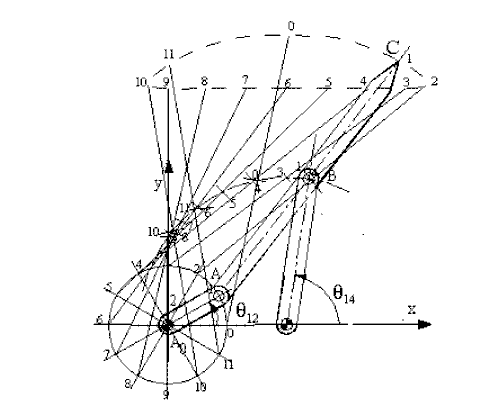
Şekilde gösterilmiş olan mekanizmayı ele alalım. Bu mekanizmada bulunan uzuvların konumunu 2 uzvunun açısal konumu θ₁₂′ iken bulalım. Vektör devre denklemi:

A₀A = A₀B₀ + B₀C + CA

olacaktır. A₀B₀ vektörünün uzunluğu ve açısı sabittir. A₀A vektörünün ise boyutu sabit olup açısal konumu bağımsız değişken θ₁₂ nin değeri ile belirlenir. B₀C vektörünün sabit bir boyu vardır. Buna karşın CA vektörünün hem boyutu hemde yönü değişecektir. Ancak B₀C ve CA vektörleri birbirlerine diktir ve daima böyle kalacaklardır (4 uzvu üzerinde A noktası anlık çakışan nokta olduğundan değişecektir, ancak CA vektör yönü 4 uzvu üzerinde kayar çift ekseni olduğundan daima B₀C vektörüne diktir). ACB₀ noktaları daima bir dik açılı üçgeni oluşturacaktır. Dört çubuk mekanizmasında yapıldığı gibi A₀ ve B₀ noktalarını yerleştirdikten sonra ilk olarak verilen θ₁₂′ açısı ile A′ noktasını yerleştirilmiş olan A₀ ve B₀ noktalarına göre yerleştirelim. B₀ merkezli, B₀C yarıçaplı daireyi çizelim. A′ noktasından bu daireye teğet çizildiğinde kesişen nokta C noktası olacak ve ∠ACB₀ açısı dik açı olacaktır. Bu şekilde 3 ve 4 uzuvlarının yeni konumları belirlenmiştir.

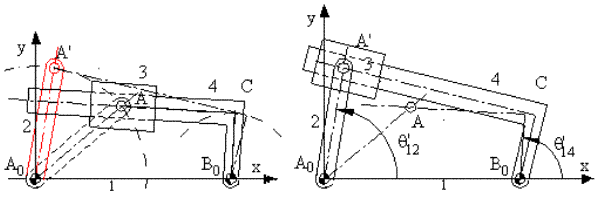
Mekanizmanın tam bir devir için hareket analizi yapılması istenildiğinde, belirli derece aralıklarda yukarıda anlatılmış olan işlemler tekrarlanır. Böyle bir analiz ile mekanizmanın animasyonu gerçekleştirilebilir ve var ise sınır konumları (örneğin θ₁₂ değerinden sonra saat yelkovanı yönünde veya ters yönünde mekanizmanın kilitlendiği konumları) veya 4 uzvunun dönme yönünü değiştirdiği θ₁₂ değerleri belirlenebilir.

Örnek:

Şekilde gösterilmekte olan krank-biyel mekanizmasını ele alalım. Bağımsız değişken 2 uzvunun 1 sabit uzvuna göre açısal konumudur. Vektör devre denklemi:

A₀A + AB = A₀Q + QB

Karmaşık sayılar ile (a₂ = |A₀A|, a₃ = |AB|)

a₂e^iθ₁₂ + a₃e^iθ₁₃ = ic + s₁₄

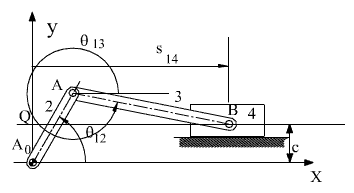
Dikkat edilir ise, s₁₄ konum değişkeni ile A₀Q sabit uzaklığı (eksantriklik; 1 uzvu üzerinde A₀ döner mafsalının kayar mafsal eksenine dik uzaklığı = c) ayırmak için A₀B vektörü dik bileşenleri ile yazılmıştır. Bu vektör devre denkleminde, AB vektörünün yönü ve QB vektörünün boyutu bilinmeyen konum değişkenleridir.

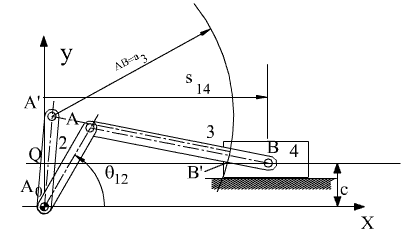
Bu mekanizmanın verilen bağımsız parametre değerine göre her hangi bir konumunu bulmak için ilk olarak A noktasının konumu belirlenir (A′). B noktasının yörüngesi sabit uzva göre kayar çift ekseni olacağından ve A noktasına uzaklığı (AB) sabit olduğundan, belirlenen A noktası merkezli AB yarıçaplı yay çizildiğinde kayar çift eksenini B noktasında kesecektir (B′).

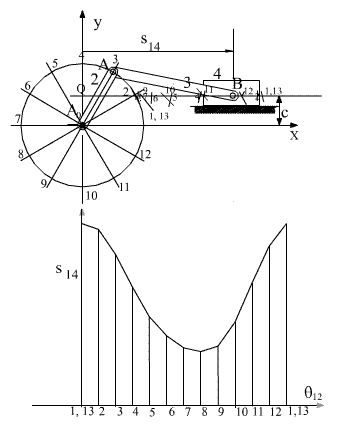
Problemi sistematik olarak çözmek için, A₀ merkezli A₀A yarıçaplı daire, A noktasının değişik krank açıları için geometrik yerini verecektir. Açıyı belirli sayıda aralıklara bölelim (genellikle bu bölme, istenilen hassasiyete göre 5° veya daha ufak aralıklarda yapılır. Ancak yöntemi göstermesi ve şeklin dahada karmaşık olmaması için şekilde 30° aralıklar seçilmiştir). Belirlenen bu A noktalarının değişik konumlarına A_i diyelim (i = 1, …, 12). A_i merkezli ve AB yarıçaplı daire yayları çizdiğimizde her bir yay kayar mafsal ekseni ile B_i noktasında kesişecektir. Bundan sonra pistonun (4 uzvu) krank dönmesine göre hareket diyagramı isteniyor ise, her konum için s_14i uzaklığı ölçülerek belirli bir ölçekte çizilebilir.

Herhangi bir konum değişkeninin bağımsız konum değişkenine göre değişimini gösteren diyagrama hareket diyagramı denir. Eğer bağımsız değişkenin zamana göre değişimi sabit ise (sabit hızda tahrik) bu durumda hareket diyagramında her hangi bir noktada eğim o konum değişkeninin o an için zamana göre değişimini (türevini, açısal hızını) verecektir. Bu diyagramlar kullanılarak mekanizmaların sınır konumlarını veya kritik durumları belirlemekte mümkündür.

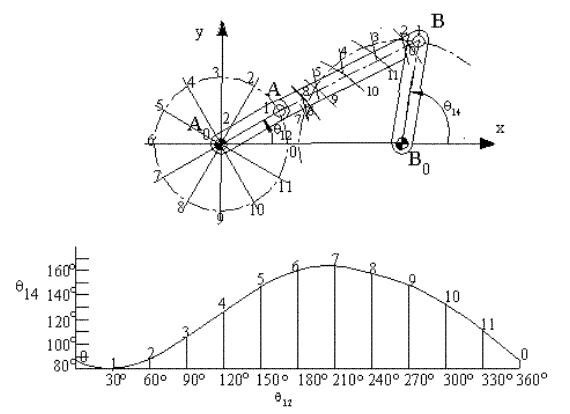
Yukarıda bir dört çubuk mekanizmasında 2 uzvunun açısal yer değişimine göre 4 uzvunun açısal yer değişimi gösterilmektedir. Başka uygulamalarda sabit uzva bağlı olmayan uzvun (biyel uzvu) her hangi bir noktasının yörüngesi önemli olabilir.

(|A₀A| = 1, |A₀B₀| = 2, |AB| = |B₀B| = |BC| = 2.5 birim)

Yukarıda hareketinin belirli bir kısmında biyel noktası yörüngesi yaklaşık bir doğru olacak şekilde tasarlanmış bir dört-çubuk mekanizmasında bu biyel noktasının yörüngesi görülmektedir. Bu eğriler biyel eğrileri olarak adlandırılır.

Grafik analiz pergel, cetvel gibi çizim aletleri ile yapılabildiği gibi, AutoCad^®, SolidWorks^®, Creo^®, Catia^®, NX^® gibi çeşitli paket programlar kullanılarak bilgisayar ortamında da yapılabilir ve mekanizmanın şekli veya montaj resmi çizildikten sonra simülasyonu da yapılabilir. Grafik analiz bilhassa konuya yeni başlayanlara kavramları görsel olarak verdiğinden çok yararlı olmaktadır.

Farklı uygulamalar internette çeşitli sitelerde bulunmaktadır. Geogebra ve Excel kullanarak hareket, hız ve ivme analizi konularında örnekler hazırlanmış ve: https://www.youtube.com/c/MuhendislerIcinExcelveGeogebraEresSoylemez Youtube kanalında yayınlanmıştır. Okuyucuların bu kanaldaki videoları izlemesi tavsiye olunur.

Örnek:

Geogebra yazılımı kullanıcının birçok siteden yasal olarak ücretsiz bir programdır. Bu program son yıllarda birçok ülkede lise seviyesinde bile matematik ve geometriyi öğretmek için kullanılmaktadır. Program istendiğinde kişisel bilgisayarınıza indirilebildiği gibi, internet ortamında da kullanılabilmektedir. Burada basit bir örnekle Geogebranın mekanizmaların analizinde ve simülasyonunda kullanımı anlatılacaktır.

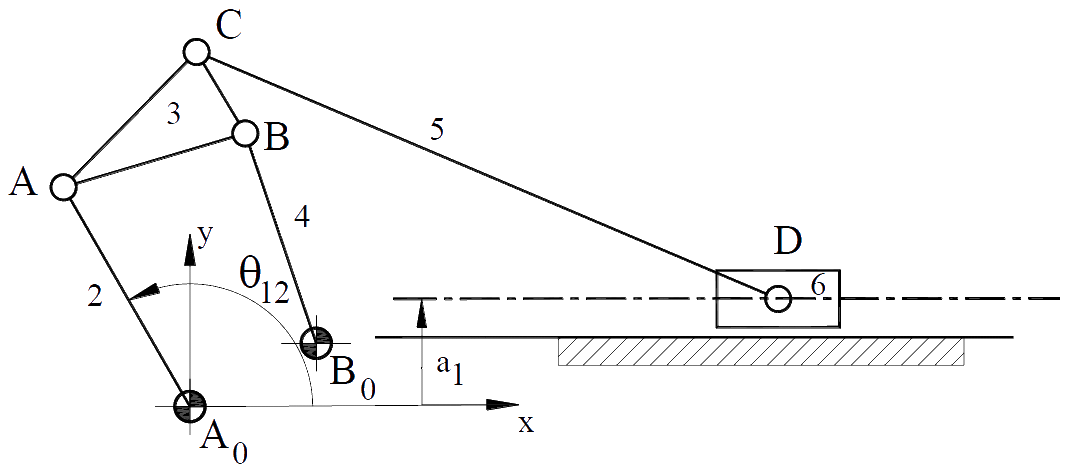
Şekilde gösterilen mekanizmanın her θ₁₂ açısında tüm uzuvlarının konumunu bulmak istiyoruz. Mekanizma uzuv boyutları: |A₀A| = 400 , |AB| = 300 , |AC| = 300 , |BC| = 150 , |B₀B| = 350 , |A₀B_0x| = 200 , |A₀B_0y| = 100 , |CD| = 1000 , a₁ = 170.

Geogebra ekranı açıldığında ilk olarak A₀ ve B₀ döner mafsal eksenlerini yerleştirmek için A_0=(0,0) ve B_0=(200,100) olarak yazalım. Kayar mafsal ekseni için Q=(0,100) diyelim ve bu noktayı belirledikten sonra doğru komutunda bulunan dik çizgi komutu ile y eksenine dik Q dan geçen doğruyu çizelim (veya, Q notasından geçen x eksenine paralel doğru olarak da bu doğruyu çizebiliriz). Ekran aşağıdaki şekilde de görüldüğü gibi olacaktır. Cebir kısmında girdiğiniz bilgiler ve Grafik kısmında ise şu anda belirlediğiniz noktalar ve çizgi görülecektir.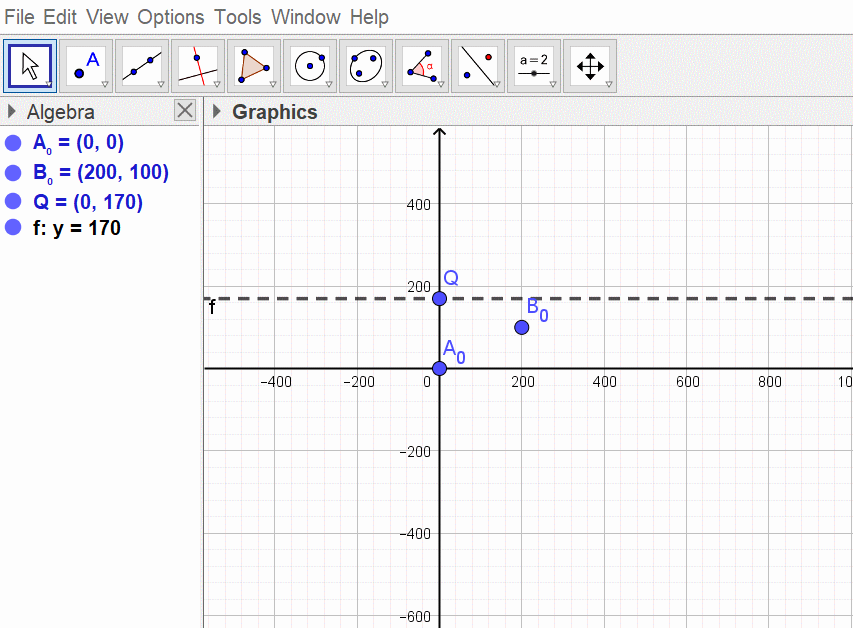

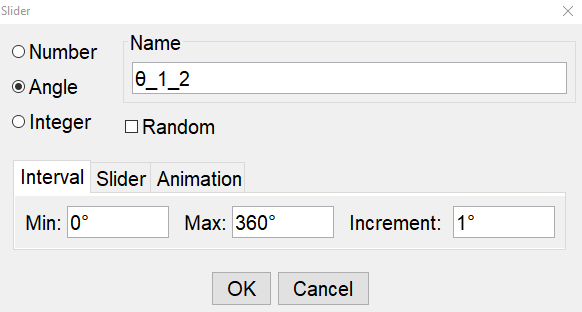
Şimdi Sürgü komutunu seçelim. Şekil 2.28 de görülen küçük ekranda değişken olarak açıyı seçelim. Bu açının başlangıç ve bitiş değerlerini ve değiştirme birimini girebilirsiniz. Ayrıca, genellikle programın kendisinin verdiği bir sembol yerine siz isterseniz kendi sembolünüzü girebilirsiniz. Bir sembol girmek için Alt tuşu ile birlikte θ için t, ϕ için f, v.b. harflerini seçersiniz. İndis yazmak için θ₁₂ için Alt+t den sonra _1_2 şeklinde yazmanız gerekir.

Şimdi girdi olarak A=(400; Alt+t_1_2) yazalım. Noktalı virgül Geogebra’ya boyut ve açı girdiğimizi belirtir (kutupsal koordinatlar). Bu şekilde A₀ dan 400 birim uzakta ve x ekseni ile θ₁₂ açısı yapan bir nokta belirlemiş oluruz. A ve A₀ noktaları arasında çizgi çizdiğimizde krankımızı göstermiş olacağız. Şimdi merkezi ve yarı çapı verilen bir daire komutunu seçelim ve A dan AB uzunluğunda (300) ve B₀ dan B₀B uzunluğunda (350) daireleri çizelim. Bu iki daire iki noktada kesişecektir. Şekilde verilen mekanizma görüntüsüne göre uygun kesim noktasını seçelim. Geogebra farklı isim verebilir. Yeniden adlandırarak bu noktayı B olarak belirleyelim. Daireleri “Show object” komutu ile gizleyebiliriz. C noktasını belirlemek için 3 uzvu üzerinde iki nokta tanımlanmış olduğundan (A ve B noktaları) A dan AC yarıçaplı, B den BC yarıçaplı dairelerin kesim noktası bize C noktasını verecektir. Yine daireler iki noktada kesiştiğinden uygun olan kesişme noktasını seçmemiz gerekir. Şimdi Çokgen komutunu kullanarak ABC üçgenini ve çizgi iki nokta arası doğru komutu ile B₀B doğrusunu çizersek, mekanizmayı oluşturan birinci devreyi çizelim. Şimdi, C noktasından CD yarıçaplı (1000) daireyi çizelim ve Kayar mafsal ekseni için çizdiğimiz çizgi ile kesim noktasını Belirleyip bu noktaya D diyelim. D noktasından kızak eksenine dik bir doğru çizdikten sonra P_1 = D + (100,50) diyerek bir P₁ noktasını belirleyelim (P₁, çizeceğimiz dikdörtgenin bir kenarı olacaktır, D den x ve y uzaklığını istediğiniz değerler seçebilirsiniz). P₁ noktasını belirledikten sonra bu noktanın yatay ve dikey eksenlerde görüntülerini alırsak dörtgenin dört köşesini elde edip bir çokgen çizebiliriz. Sonuç aşağıdaki şekilde görülmektedir.

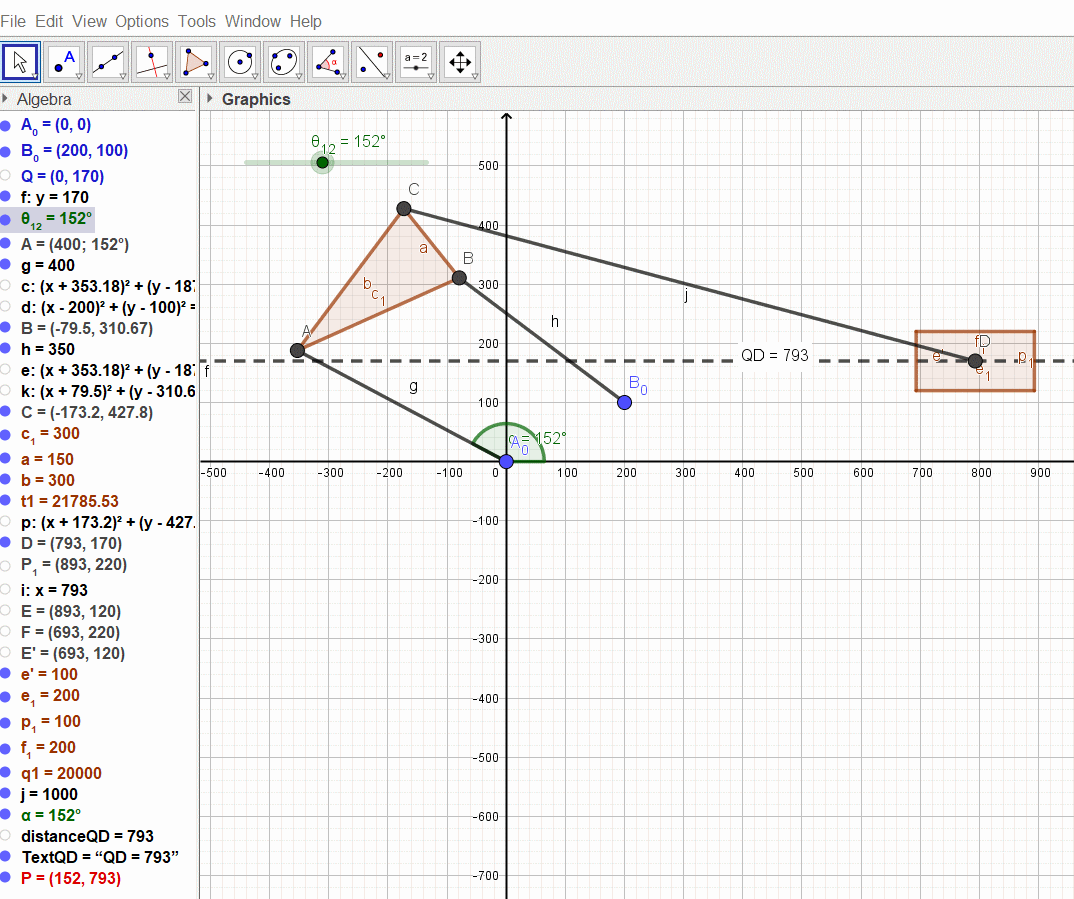
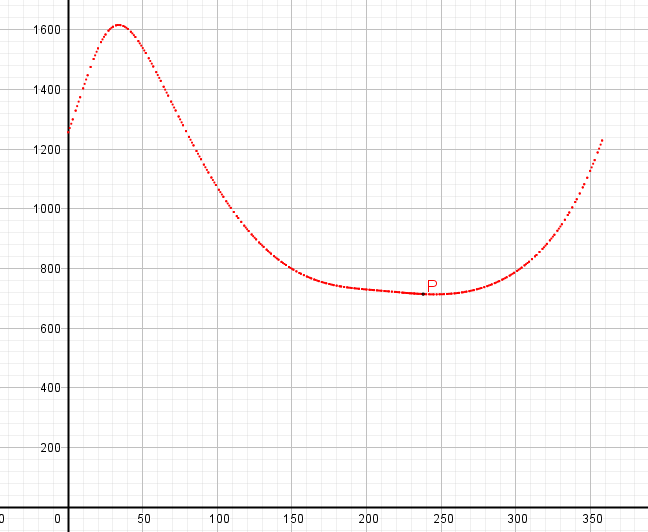
6 uzvunun krank dönme açısına göre hareket eğrisini görmek istediğimizde, ilk olarak A₀A doğrusunun x eksenine göre açısını ve D noktasının Q noktasından uzaklığını belirleriz. İkinci bir grafik alanı açalım. Bu yeni grafik alanda sadece P=(a*180/p, DistanceQD) olarak bir nokta çizelim. Mekanizmanın animasyonu için sürgüyü oynama durumuna getirdiğimizde P noktasının konumu ikinci grafikte değişecektir. Bu noktayı “İzle” meye aldığımızda aşağıdaki şekilde görüldüğü gibi, hareket eğrisi elde edilecektir. Bu noktanın koordinatlarını başka bir yerde kullanmak istediğinizde listeleme (SpreadSheet) sayfası açırak P noktasının koordinatları bir dosyaya yazılabilir, başka bir program tarafından kullanılabilir).

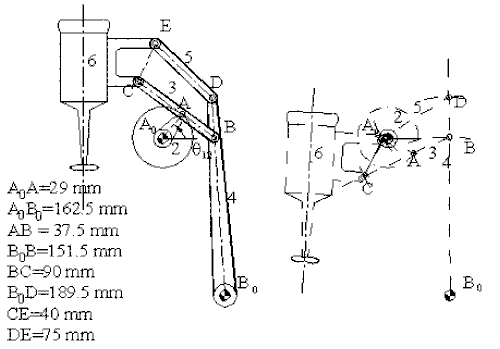
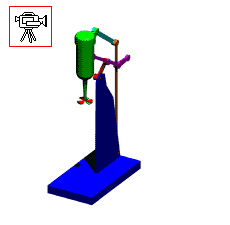
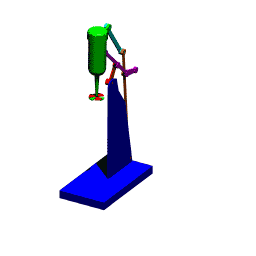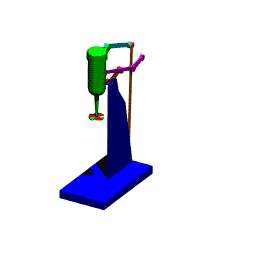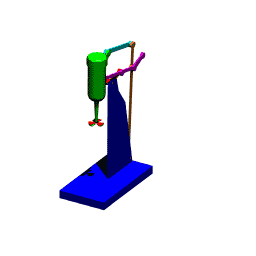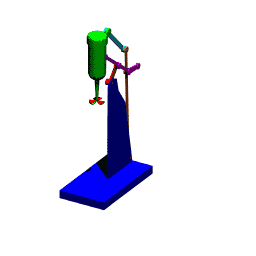
Mekanizmada birden çok devre var ise, bu devreler çoğunlukla teker teker çözülebilir. Yukarıda gösterilen mekanizma bir karıştırıcıyı yukarı-aşağı hareket ettirmek içindir. A₀A uzvuna bir kol bağlı olup hareket elle bu uzva verilir.

A₀ABB₀ (1, 2, 3 ve 4 uzuvları) birinci devreyi oluşturmaktadır. Vektör devre denklemi (B mafsalını söküp takarak):

A₀A + AB = A₀B₀ + B₀B

Bu vektör devre denklemi A₀A uzvunun yeni bir konumu için bir dört-çubuk mekanizmasında gösterildiği gibi çözülebilir ve B noktasının konumu bulunur. C noktası 3 uzvu ve D noktası 4 uzvu üzerinde olduğundan yeni AB konumları belirlendikten sonra sabit uzuv boyutları kullanılarak C ve D noktalarının yeni konumları bulunur (3 uzvu üzerinde B ve A noktalarının konumu bilindiğine ve C noktası BA doğrusu üzerinde olup B den 90 mm uzakta olduğuna göre C noktasının konumu ve D noktası 4 uzvu üzerinde olduğuna, bu uzuv üzerinde B ve B₀ noktalarının konumu bilindiğine, D noktası B₀B doğrusu üzerinde ve B₀ dan 189.5 mm uzakta olduğuna göre D noktasının konumu belirlenir).

İkinci olarak BCEDB (3, 6, 5 ve 4 uzuvları) devresini göz önüne alalım. Bu devre için vektör devre denklemi:

BC + CE = BD + DE

yazılabilir. Bu vektör devre denkleminde BC ve BD gerek uzunluğu ve gerek yönü bilinen iki vektördür. CE ve DE vektörlerinin ise boyutları uzuv boyutu olduğundan bilinmektedir. C ve D noktaları birinci devre denkleminin çözülmesi ile yukarıda açıklandığı gibi belirlendikten sonra, üç kenarı bilinen CED üçgenini çizmemiz gerekmektedir. Öyle ise C merkezli CE yarı çaplı bir daire yayı ile D merkezli DE yarı çaplı daire yayının kesişme noktası E noktasının ve dolayısı ile tüm uzuvların konumunu belirler (her uzuv üzerinde iki noktanın konumu belirlenmiş olur).

 

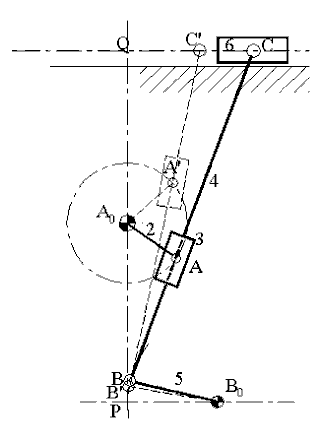
Bazı karmaşık mekanizmalarda konum analizi her bir devrenin ayrı ayrı ve sıra ile çözülmesi mümkün olmayıp, örneğin iki devrenin birlikte çözümü gerekebilir. Bu durumlarda devre denkleminin grafik çözümü deneme-yanılma yöntemini gerektirecekti. Örneğin yukarıda görülen mekanizma için devre denklemleri:

PA₀ + A₀A = PB₀ + B₀B + BA

PQ + QC = PB₀ + B₀B + BC

şeklinde yazılabilir. Her iki denklemde de üç bilinmeyen konum parametresi bulunmakta, toplamda ise dört bilinmeyen konum parametresi bulunmaktadır. (A₀A kol açısı verildiği kabul edilmektedir. Birinci denklemde: B₀B nin açısal konumu, BA nın hem açısal konumu ve hemde boyutu; İkinci denklemde ise, QC boyutu, B₀B nin açısal konumu, BC nin açısal konumu bilinmeyen konum parametreleridir. BC ve BA vektörlerinin açısal konumu aynı olduğundan, toplam 4 bilinmeyen konum parametresi vardır.

B noktasının geometrik yeri B₀ merkezli B₀B yarıçaplı bir daire yayıdır. C noktasının geometrik yeri ise kayar mafsal ekseni olan doğrudur. Giriş kolunun açısal konumu belirlendiğinde konumu belli olan A noktası ise BC doğrusu üzerinde olmalıdır. Deneme yanılma ile BC uzunluğu sabit doğruyu B ve C yörüngelerini sağlayacak şe-kilde hareket ettirerek A noktasının Bu doğru üzerinde bulunduğu konumu bulmamız gerekmektedir. Sağlanması gerekenler:

a) B noktası B₀B yarıçaplı ve B₀ merkezli bir yay üzerinde olmalıdır.

b) C noktası kayar mafsal ekseni ile belirtilen doğru üzerinde olmalıdır.

c) 4 uzvunu belirleyen BC doğrusunun A₀A boyutu ve giriş kolu açısı ile belirlenmiş olan A noktasından geçmesi gerekmektedir.