3.3 Çakışan Noktalar

Mekanizmalarda bir çok rijit cisimden (uzuvdan) oluşan bir sistem vardır. Bu uzuvlar arasında bağıl hareket, uzuvları birbirlerine bağlayan mafsalların serbestlik derecesi ve tipi ile belirlidir. Yukarıda rijit cisimler için elde edilen üç sonuca göre her bir uzuv sonsuz boyutlu kabul edilebileceğinden krank-biyel mekanizması için şekilde gösterildiği gibi, mekanizmayı oluşturan uzuvları hafızamızda üst üste duran sonsuz boyutlu düzlemlerden oluştuğunu düşünmemiz gerekir.

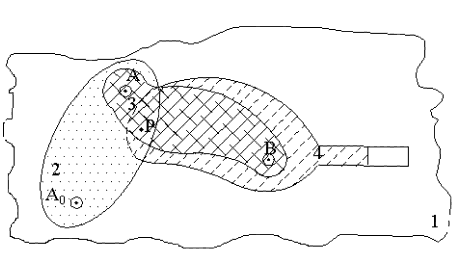
2 uzvunun 1 uzvuna göre hareketini inceleyelim. 2 uzvu 1 uzvuna A₀ noktasından geçen bir eksene sahip döner mafsal ile bağlı olduğundan, 2 uzvu 1 uzvuna göre sadece dönme hareketi yapabilecektir. Mafsalın çapı, uzvun büyüklüğü bu bağıl hareketin şeklini hiç bir şekilde etkilemez. Benzer bir yaklaşım ile 3 uzvunun 2 uzvuna göre ve 4 uzvunun 3 uzvuna göre bağıl hareketleri sırası ile A ve B noktalarından geçen, düzleme dik bir eksen etrafında dönme olacaktır. 4 uzvunun 1 uzvuna göre hareketi ise iki uzuv birbirlerine kayar mafsal ile bağlı olduklarından kayar mafsal ekseni yönünde öteleme hareketidir.

Üst üste düzlemlerden oluşan bu mekanizmaya bir iğne batıralım (şekilde gösterilen P noktası). Bu iğne, mekanizmada 4 uzuv olduğundan, bu uzuvlara bağlı 4 düzlemi de delecektir. Öyle ise 1 uzvu üzerinde P₁, 2 uzvu üzerinde P₂ , 3 uzvu üzerinde P₃ ve 4 uzvu üzerinde P₄ noktaları bulunacaktır. 1 uzvu üzerinde alınan sabit bir referans eksenine göre bu 4 noktanın konumu aynıdır ve aynı konum vektörü ile gösterilir. Mekanizmanın bir miktar bu ilk konumdan yer değiştirdiğini düşünelim. P₁ noktası, sabit uzuv üzerinde olduğundan, konum vektörü sabit olacak ve konumunu değiştirmeyecektir. 2 uzvu sabit uzva göre A₀ noktası merkez olmak üzere döndüğünden P₂ noktası A₀ merkezli PA₀ yarıçaplı bir daire üzerinde hareket edecektir. Benzer bir şekilde P₂ noktasının 3 uzvu üzerinde izdüşümünü incelersek, bu sefer A merkezli AP yarıçaplı bir daire üzerinde olacaktır. P₂ noktasının 4 uzvu üzerinde çizdiği yörünge basit bir daire olmayacaktır (genellikle krank-biyel mekanizması için bu dördüncü mertebeden bir eğridir). Benzer incelemeyi P₃ ve P₄ noktaları için de yapabiliriz.

Şimdi B noktasını göz önüne alalım. Dört nokta (B₁, B₂, B₃ ve B₄), o an için çakışmaktadır. B noktası 3 ve 4 uzuvları arasında bulunan döner mafsalın eksen doğrusu üzerinde olduğundan B₃ ve B₄ noktaları her konum için çakışacaktır. Buna daima çakışan noktalar diyeceğiz. Buna karşın B₂ ve B₁ noktaları sadece inceleme anında diğer iki nokta ile çakışacak, mekanizmanın başka bir konumunda B₃ ve B₄ hala çakışık iken B₂ ve B₁ in konumları farklı olacaklardır. Bu özellikte olan noktalara anlık çakışan noktalar diyeceğiz.

Mekanizmaları yukarıda gösterildiği gibi çizmek yaygın bir uygulama şekli değildir. Mekanizma uzuvları ya gerçek uygulamada aldıkları şeklin teknik resim kurallarına göre çizilmesi ile (bu şekilde çizmek mekanizmanın kinematik analizi sırasında oldukça zordur) veya basit geometrik şekiller olarak sadece mafsal noktalarını ve ilgilendiğimiz bir nokta veya çizgiyi içerecek şekilde çizilirler.

Analiz sırasında her uzvun sonsuz boyutta olabileceği unutulmamalıdır.