Düz yüzeyli öteleme yapan izleyicili radyal kam profilinin elde edilmesi:
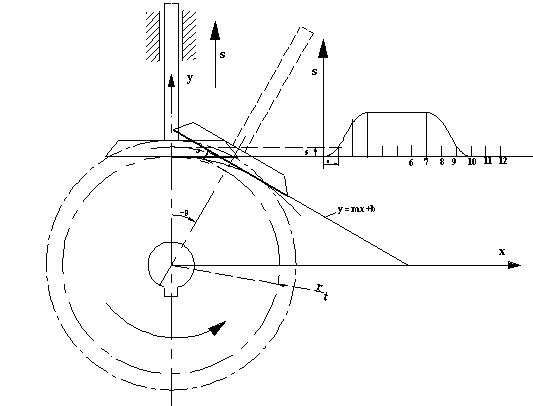
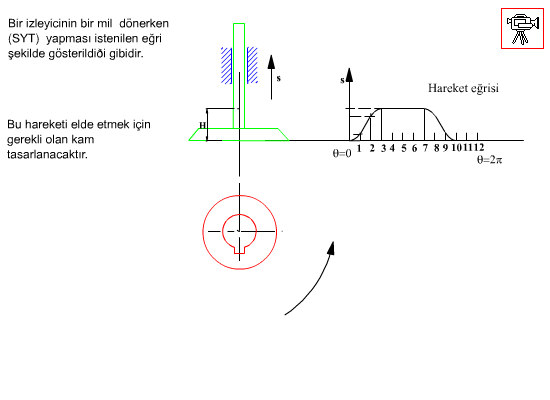
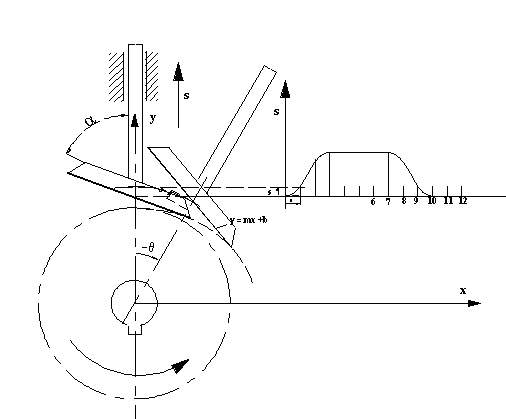
Şimdi zarf teorisini düz yüzeyli öteleme yapan radyal kam için uygulayalım. Hareket eğrisi s(θ) ve ve türevleri kamın tam bir devri için bilinmektedir. Her hangi bir θ açısı ve buna karşı gelen s yükselme uzunluğunda izleyicinin kama göre bağıl konumu yukarıda görülmektedir.
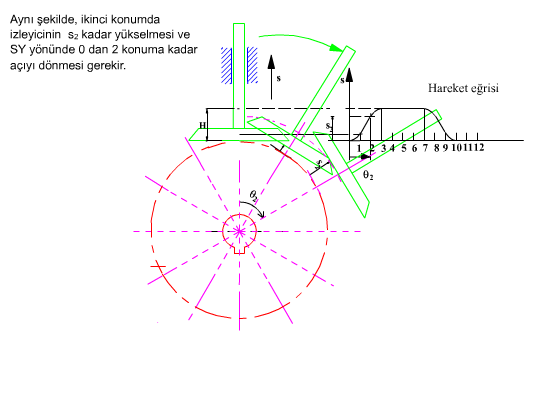
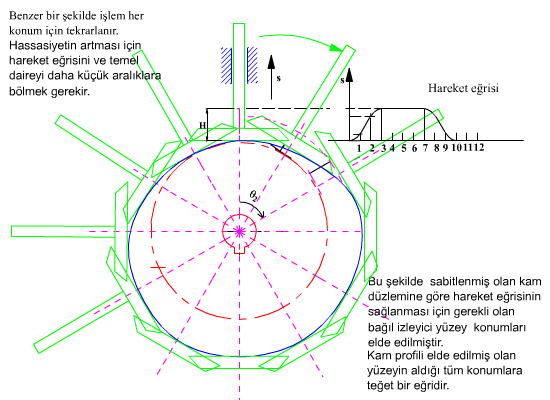
Şekilde görüldüğü gibi, düz yüzeyli bir izleyicinin kama göre bağıl konumları, doğrulardan oluşan bir eğri demetini oluşturur. Bu doğru:
y = mx + b
şeklinde yazılabilir. Burada:
m = −tanθ : doğrunun eğimi
b = (rt + s)/cosθ : y ekseni kesim noktası
dır. Bu durumda eğri demeti:
f(x, y, θ) = y cosθ + x sinθ − (rt + s) = 0
dır. Denklemin θ parametresine göre türevi:
fθ(x, y, θ) = −y sinθ + x cosθ − ∂s/∂θ = 0
Bu iki denklemden x ve y koordinatları için çözüm yapıldığında
x = (rt + s) sinθ + cosθ
y = (rt + s) cosθ − sinθ
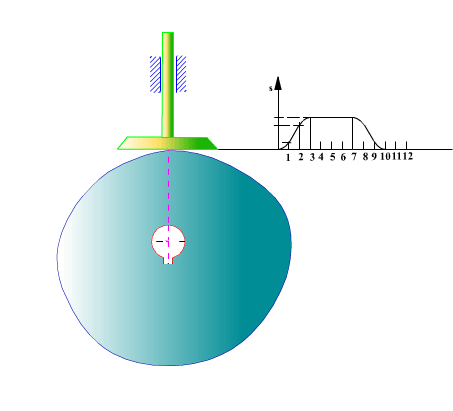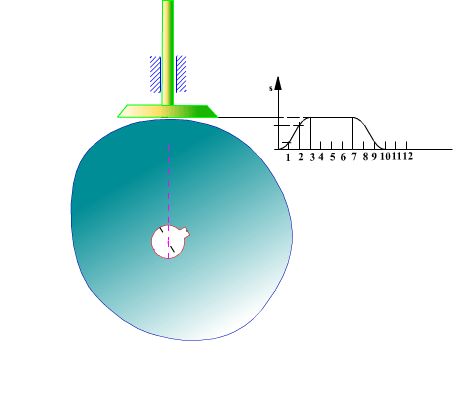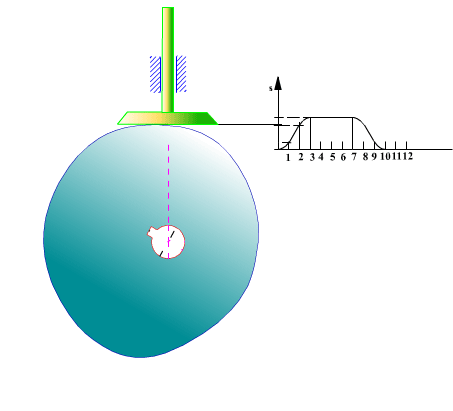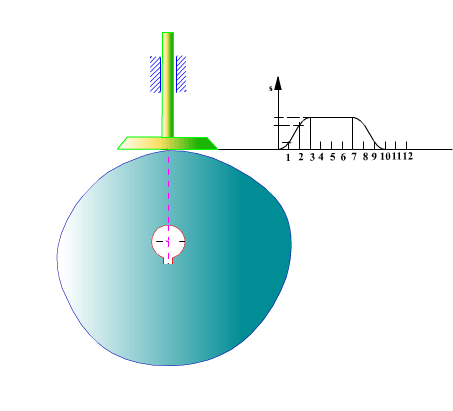
Dikkat edilir ise, toparlaklı izleyicinin aksine, düz yüzeyli izleyici için tek bir kam yüzeyi (zarf eğrisi) elde edilmistir.
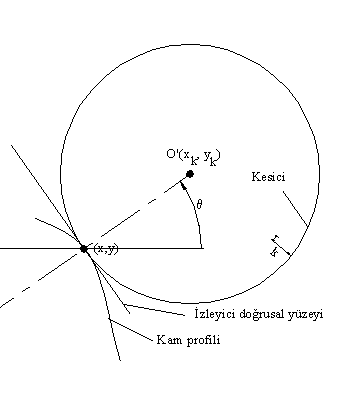
Bu kam profilini rk yarıçaplı bir kesici çakısı ile işlememiz gerektiğinde, kesici ekseni koordinatları gerekecektir. Kesici dairesi kam profiline değdiği noktada profile teğet olmalıdır. Şekilden:
xk = x + rk cosθ
yk = y + rk sinθ
olacaktır. Burada θ kam dönme açısıdır.
Siz de, benzer denklemleri düz izleyici yüzeyinin öteleme ekseni ile α açısı yaptığı durum için elde edin ve α = 90° için yukarıda verilmiş olan denklemleri elde edin.
Örnek 8:
Temel daire yarıçapı 50 mm olacak şekilde düz yüzeyli izleyici kullanıldığında, Örnek 5 te istenilen hareket eğrisini elde etmek için gereken kam profilini bulalım. Örnek 5 te verilen hareket eğrisi ve türevi aynen kullanılacaktır. Kam profili koordinatları:
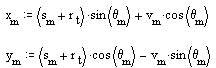
olacaktır. Polar koordinat takımına göre:

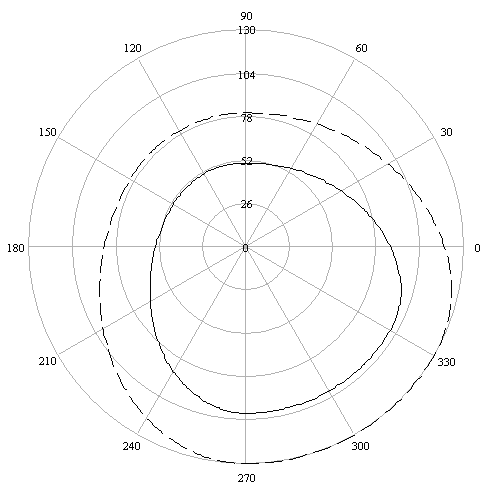
Kam profili ve kesici eksen takımı yörüngesi (kesik çizgi) şekilde gösterilmektedir. Dikkat edilir ise, belirli bir toparlak çapı için imal edilmiş kam mekanizmasinda farklı çapta bir toparlak kullanılır ise, istenilen ve tasarlanan hassas hareket eğrisinin elde edilmesi söz konusu değildir.