Toparlaklı, salınım yapan izleyicili radyal kam profilinin elde edilmesi:

 

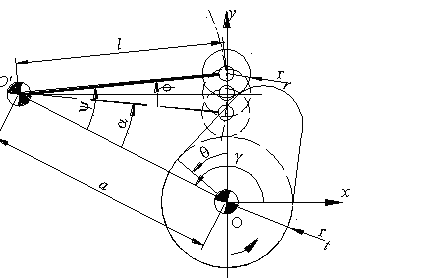
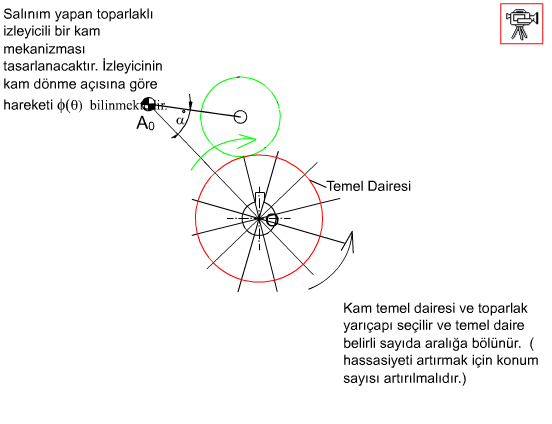
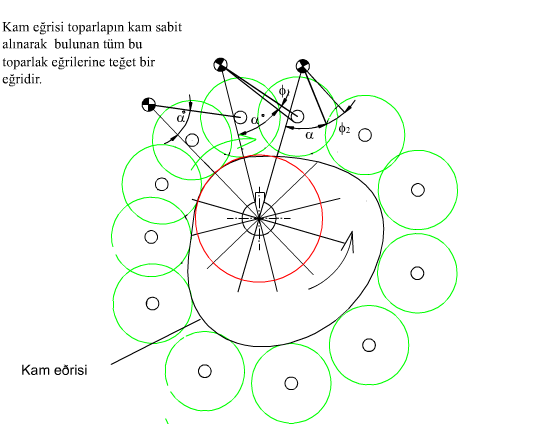
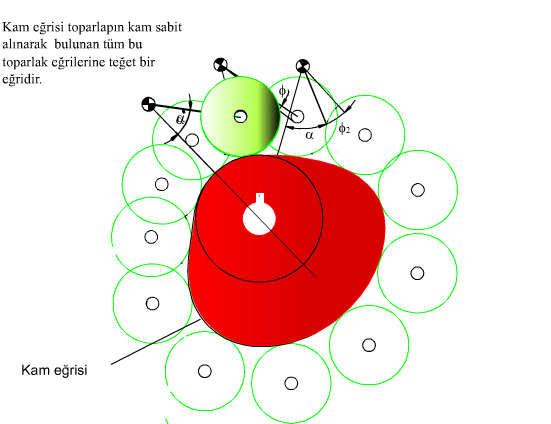
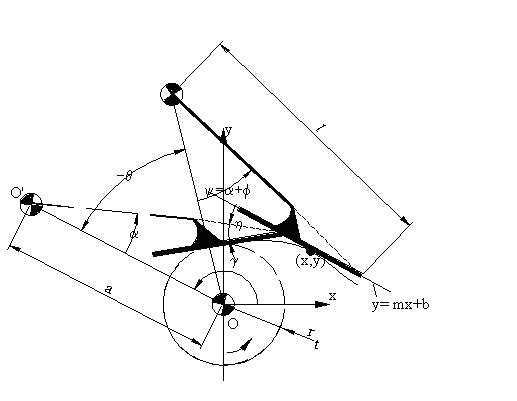
Toparlaklı salynım yapan izleyicili kam mekanizmasının genel şekli yukarıda görülmektedir. İzleyicinin yaptığı toplam salınım açısı ϕ₀ ötelemede H yüksekliğine karşı gelecektir. Toparlak merkezi O′ merkezli daire yayı üzerindedir ve eger a ve l belirli uzunlukta ise, toparlak merkezinin çizdigi daire yayı bir doğruya çok yakındır. Salınım açısının orta noktasinda izleyici kolu toparlak merkezinden kam merkezine çizilen doğruya dik alinir ise, mekanizma s = lϕ olacak şekilde öteleme yapan izleyici şeklinde yaklaşık olarak düşünülebilir ve öteleme yapan izleyicili kam mekanizması için gösterilmiş olan bağlama açısı hesapları benzer bir şekilde kamın temel daire yarıçapını bulmak için kullanilabilir.

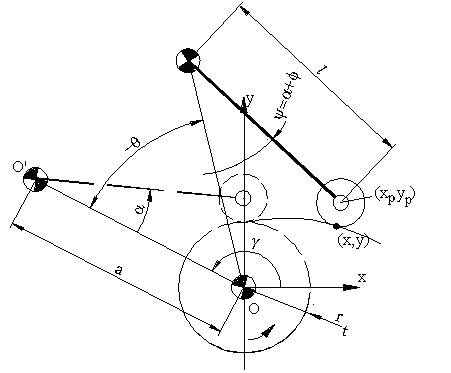
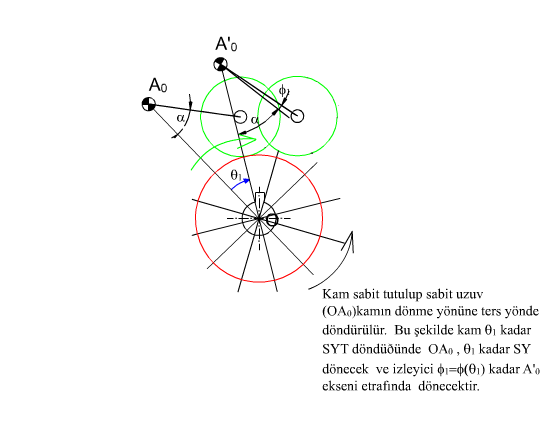
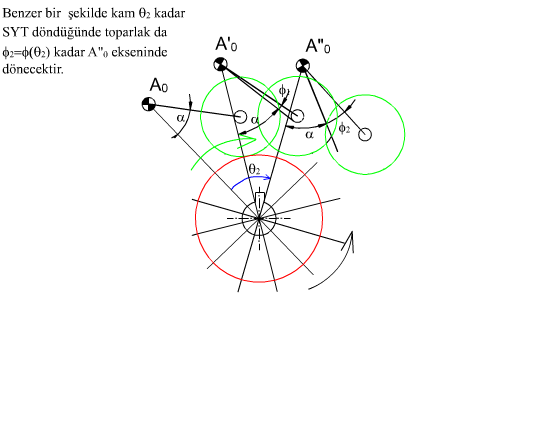
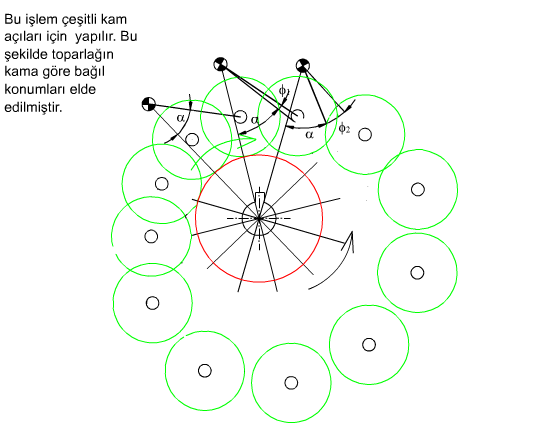
Geometrik olarak profili belirleme yukarıda gösterilmektedir. Genel bir konumdaki durumu ele alalım. Kam profilinin bulunmasi sırasında öteleme yapan izleyicide olduğu gibi, kam sabit tutulacak ve sabit uzuv kam hareketine ters yönde hareket ettirilecektir. Egri demetini olusturan toparlagin daire denklemi:

f(x, y, θ) = (x − x_p)² + (y − y_p)² − r_r = 0                                     (1)

şeklinde yazılabilir. Bu denklemde toparlak merkezini bulmak için kompleks sayı kullanıldığında:

z = x_p + iy_p = ae^{−i(γ − θ)} − le^{i(γ + α + ϕ − θ)}

veya

x_p = a cos(γ − θ) − l cos(γ + α + ϕ − θ)

_yp = a sin(γ − θ) − l sin(γ + α + ϕ − θ)                                      (2)

olacaktır. Bu denklemde:

α = cos^-1[(a² + l² − (r_r + r_t)²)/(2al)]

dir. Bir kam mekanizmasi için α ve γ sabit değerler olup ϕ izleyici salınımı hareket eğrisi ile verilen θ nın fonksiyonudur. Eğri demeti denkleminin θ parametresine göre türevi:

f_θ(x, y, θ) = −2(x − x_p)∂x_p/∂θ − 2(y − y_p)∂y_p/∂θ = 0                    (3)

olacaktır. Bu denklemde:

∂x_p/∂θ =  a sin(γ − θ) + l sin(γ + α + ϕ − θ)(∂ϕ/∂θ − 1)

∂y_p/∂θ =  −a cos(γ − θ) − l cos(γ + α + ϕ − θ)(∂ϕ/∂θ − 1)

(1) ve (3) denklemlerinden kam profili koordinatları (x, y) her θ açısı için:

x = x_p ± \displaystyle \frac{{{{\text{r}}_{\text{r}}}}}{{\sqrt{{1+{{{\left( {\frac{{\partial {{\text{x}}_{\text{p}}}\text{/}\partial \text{θ}}}{{\partial {{\text{y}}_{\text{p}}}\text{/}\partial \text{θ}}}} \right)}}^{2}}}}}}

y = y_p − (x − x_p) \displaystyle {\frac{{\partial {{\text{x}}_{\text{p}}}\text{/}\partial \text{q}}}{{\partial {{\text{y}}_{\text{p}}}\text{/}\partial \text{q}}}}

olarak elde edilir. Dikkat edilir ise, toparlaklı öteleme yapan izleyiciden farkı, toparlak daire merkezi koordinatları ve bu koordinatların θ ya göre türevleri için verilmiş olan 2 ve 4 denklemlerinin değişik olusudur. Her θ değeri için iki nokta elde edileceğinden kam eğri demetinin zarfı olan kam profili iki kısımdan oluşacaktır. Bu noktalardan birisi dıştan temas eden kam profili digeri ise içten temas eden bir kam profili üzerinde bulunan noktadır.

Benzer bir yöntem kullanarak salınan düz yüzeyli izleyicili radyal bir kam profilinin koordinatlarini belirleyin. (η açısı ve a, luzaklıkları ile temel daire çapı verilen değerler olduğunu kabul edelim).

Örnek 9:

Bir toparlaklı izleyicinin, kamın 120° (SYT) dönmesi sırasında 40° (SYT) sikloid hareket ile salınmasını, bu konumda kamın 80° dönmesi sırasında beklemesini, kamın 140° dönmesi sırasında 40° (SY) salınarak baslangıç konumuna sikloid hareket ile geri dönmesini istiyoruz. İzleyici ile kam dönme eksenleri arası 300 mm (a = 300) izleyici kol boyu 175 mm dir (l = 175). Toparlak yarıçapı 75 mm dir ( r_r = 75). Bağlama açısının 90° den en fazla sapması 30° olması gerekir.

Salınan izleyiciyi öteleme yapan bir izleyici ile benzeştirir isek:

H = l ϕ₀ = 175×40×π/180 = 122 mm dir.

Yükseliş sikloidal hareket olduğuna göre Normalizasyon tablosundan: C_v = 2 dir. Bu durumda:

(ds/dθ)_max = C_vH/β = 2(122)/(2π/3) = 366/π = 117

olacaktır. Bu durumda:

r_p = (ds/dθ)_max tanμ_min = 117 tan60° = 203 mm

dir. r_p = r_t + H/2 + r_r olduğundan r_t + r_r = 142 mm dir. r_r = 75 mm lik bir toparlak yarıçapı düşünüldüğünde, temel daire yarıçapı en az r_t = 67 mm olur. r_t = 90 mm seçildiğinde ise μ_min = 62.6° olacaktır. Dikkat edilir ise, bağlama açısından dolayı en küçük çap belirlendikten sonra, tasarımcı mümkün olan durumlarda çapı daha büyüterek kuvvet iletimi açısından daha uygun boyutlar bulabilir. Ayrıca uygulanmakta olan yöntem bilhassa salınım yapan izleyici için yaklaşık bir hesaplama metodu olduğundan r_t = 67 mm alındığında müsaade edilen minimum bağlama açısından daha küçük bir değerle karşılaşılabilir. Bu nedenle r_t = 90 mm seçilmiştir.

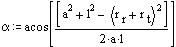
denkleminden α = 38.124° dir. İzleyici kolunun toparlak merkezi-kam merkezi doğrusuna orta noktada teğet olması için γ = 134° alınmıştır. Hareket egrisi ve türevi:

 

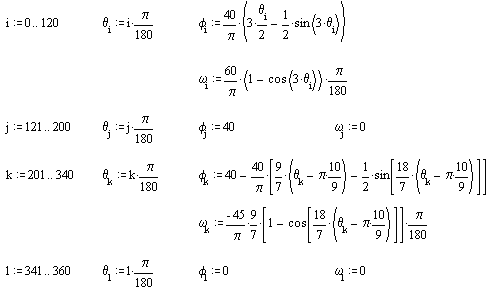
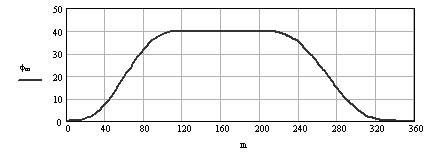
Hareket eğrisi

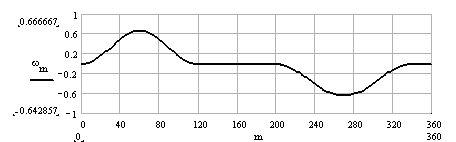
Hareket eğrisi türevi (giriş açısal hızı 1 rad/s olduğunda açısal hız)

Toparlak merkezi koordinatlari ve kam açisina göre türevleri:

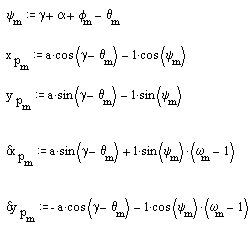
Sadece dıştan temas eden kam profilini istiyoruz. Bu profili elde etmek için:

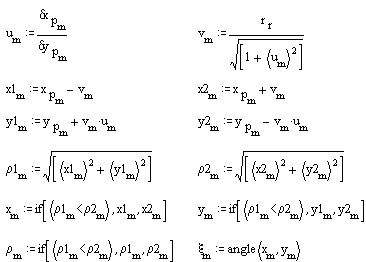
Kam profilinin 80 mm yarıçaplı bir taş ile taşlanacağı düşünüldüğünde taş merkezinin yörüngesi:

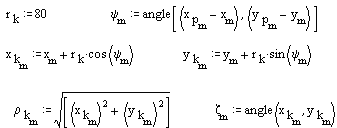
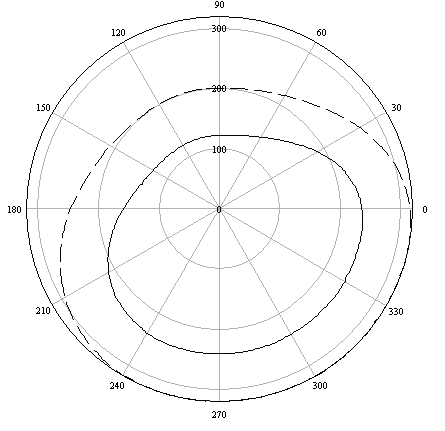
Sonuç kam profili ve kesici ekseni yörüngesi (kesik çizgi) şekilde görülmektedir. Uygulamada elde ettiğimiz koordinat değerlerinin doğrudan nümerik kontrollü tezgaha girilmesi gereklidir.

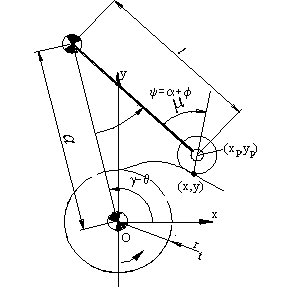
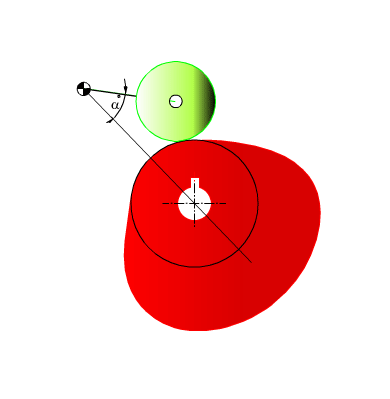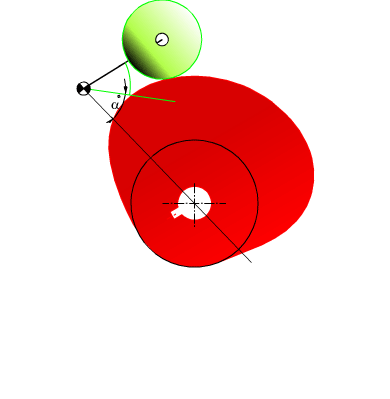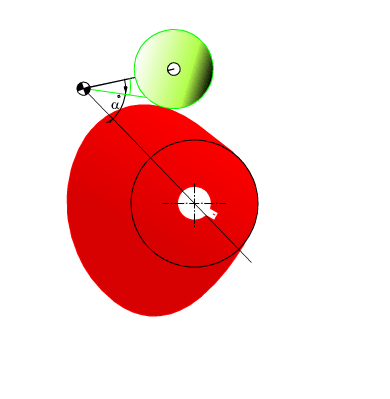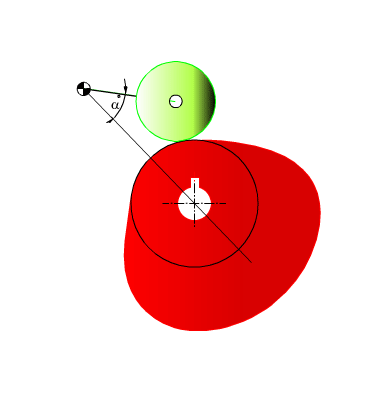
Mekanizmanın hareketi sırasında her konumda oluşan bağlama açısını yukarıda gösterilen şekli kullanarak bulabiliriz. Bu durumda bağlama açısı:

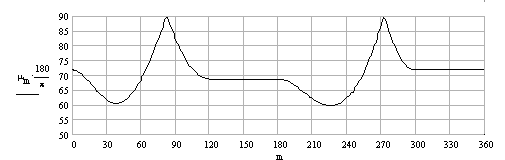
Elde edilmiş olan kam mekanizması için bağlama açısının kamın bir devrinde değişimi

En küçük baglama açısı μ_min = 60.64° dir.  Dikkat edilir ise, bu minimum değer yükselmenin tam orta noktasında olmadığı gibi, r_t = 90 mm için beklediğimiz minimum değerden küçüktür. Bu bağlama açısı hesaplamasının bilhassa salınım yapan izleyici için yaklaşık olduğuna önceden dikkat çekilmistir (optimum kam mekanizması için sadece temel daire çapı değil, sabit mafsallar arasi uzaklık (a) ve kol boyu (l) degişken kabul edilerek farklı tasarımlar elde edilebilir).