4.2 Mekanizmalarda Hız ve İvme Analizi -4
Örnek:
Şekilde gösterilmiş olan mekanizma saman balyalama makinasında kullanılmıştır. 6 uzvu üzerinde bulunan F noktasının konum, hız ve ivmesini giriş kolu 4 rad/s sabit açısal hız ile dönerken her açıda bulmak istiyoruz.
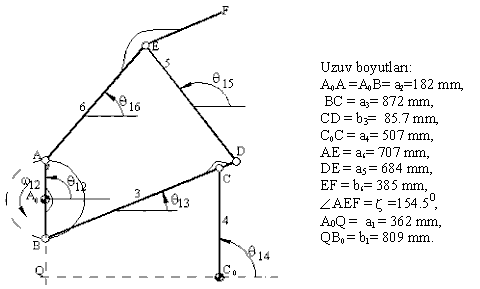
Bu problemde konum analizi için üçgen çözümleri kullanılacak, hız analizi için ise matris çözümü uygulanacaktır.
C0B = xB + iyB = −b1 − a2cosθ12 + i(a1 − a2sinθ12)
Görüldüğü gibi, xB ve yB B noktasının C0 noktasına göre, pozitif x ekseni QC0 olmak üzere, koordinatlarıdır. C0B vektörünü dik koordinat sisteminden polar koordinat sistemine dönüştürdüğümüzde:
C0B = s∠ϕ
s = \displaystyle \sqrt{{{{\text{x}}_{\text{B}}}^{2}+{{\text{y}}_{\text{B}}}^{2}}} ϕ = atan2(xB, yB)
olacaktır. BCC0 üçgeninde ∠BC0C = β ve ∠BCC0 = μ1 dersek, kosinüs teoremine göre bu açılar:
β = cos-1\displaystyle \left[ {\frac{{{{\text{s}}^{2}}+{{\text{a}}_{4}}^{2}-{{\text{a}}_{3}}^{2}}}{{2{{\text{s}}_{4}}\text{s}}}} \right]
μ1 = cos-1\displaystyle \left[ {\frac{{{{\text{a}}_{3}}^{2}+{{\text{a}}_{4}}^{2}-{{\text{s}}^{2}}}}{{2{{\text{a}}_{3}}{{\text{a}}_{4}}}}} \right]
olacaktır. θ14 ve θ13 açıları:
θ14 = ϕ − β ve θ13 = θ14 − μ1
olacaktır. Burada θ14 = ϕ − β alınması, incelenmekte olan dört-çubuk mekanizmasının bağlantı şekline uygundur. Şimdi A ve D noktalarının C0 noktasına göre konumlarını belirleyelim.
C0A = xA + iyA = −b1 + a2cosθ12 + i(a1 + a2sinθ12)
C0A = xD + iyD = a4cosθ14 + b3cosθ13 + i(a4sinθ14 + b3sinθ13)
DA = C0A − C0D = r∠χ dersek r = \displaystyle \sqrt{{{{{\left( {{{\text{x}}_{\text{A}}}-{{\text{x}}_{\text{D}}}} \right)}}^{2}}+{{{\left( {{{\text{y}}_{\text{A}}}-{{\text{y}}_{\text{D}}}} \right)}}^{2}}}} ve χ = atan2(xA − xD, yA − yD) olur. Bu şekilde bir kenarının boyutunu bulduğumuz ADE üçgeninde ∠ADE = γ ve ∠AED = μ2 dersek, kosinüs teoremine göre bu açılar:
γ = cos-1\displaystyle \left[ {\frac{{{{\text{r}}^{2}}+{{\text{a}}_{5}}^{2}-{{\text{a}}_{6}}^{2}}}{{2{{\text{a}}_{5}}\text{r}}}} \right]
μ2 = cos-1\displaystyle \left[ {\frac{{{{\text{a}}_{5}}^{2}+{{\text{a}}_{6}}^{2}-{{\text{a}}^{2}}}}{{2{{\text{a}}_{5}}{{\text{a}}_{6}}}}} \right]
olacaktır. Bulunan bu değerler kullanılarak θ15 ve θ16 açıları:
θ15 = χ − γ ve θ16 = θ15 − μ2
F noktasının A0 noktasına göre konum vektörü:
A0F = A0A + AE + EF
veya karmaşık sayılar ile:
A0F = xF + iyF = a2eiθ12 + a6eiθ16 + b6ei(θ16 + ζ + π)
Bu denklemden:
xF = a2cosθ12 + a6cosθ16 − b6cos(θ16 + ζ)
yF = a2sinθ12 + a6sinθ16 − b6sin(θ16 + ζ)
Verilen bir θ12 krank açısından başlayarak yukarıda verilmiş olan denklemler sıra ile çözülerek F noktasının konumu bulunabilir. Dikkat edilir ise, elde edilmiş olan bir çözüm algoritmasıdır ve sayısal olarak bu algoritmanın uygulanabileceği çeşitli programlama ortamında kullanılabilir. Örneğin Excel, Mathcad, Matlab gibi matematik işlem ağırlıklı paket programları veya Basic ve C gibi bilgisayar lisanları kullanarak kolaylıkla bu denklemlerle bir algoritma yapısı içinde bilgisayarda çözüm yapabilir ve sayısal değerler elde edebiliriz. Şekilde F noktasının yörüngesi görülmektedir (A0 merkez olarak) (yörünge üzerinde × ile işaretlenen nokra θ12 = 90° deki konumdur).
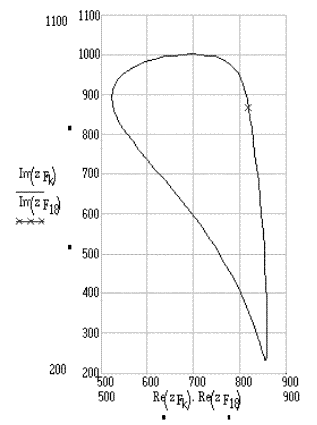
F noktasının yörüngesi
Hız ve ivme analizi için kullanılmak üzere katsayı matrisi karmaşık sayılar ile:
A = \displaystyle \left[ {\begin{array}{cccc} {\text{i}{{\text{a}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} & {-\text{i}{{\text{a}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}}}}} & 0 & 0 \\ {-\text{i}{{\text{a}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} & {\text{i}{{\text{a}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}}}}} & 0 & 0 \\ {\text{i}{{\text{c}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} & 0 & {\text{i}{{\text{a}}_{5}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{15}}}}}}} & {-\text{i}{{\text{a}}_{6}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{16}}}}}}} \\ {-\text{i}{{\text{c}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} & 0 & {-\text{i}{{\text{a}}_{5}}{{\text{e}}^{{-\text{θ}{{\text{θ}}_{{15}}}}}}} & {\text{i}{{\text{a}}_{6}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{16}}}}}}} \end{array}} \right]
dir. Hız denklemi:
AΩ = b
olup burada:
Ω = [ω13 ω14 ω15 ω16]T ve b = [ia2ω12eiθ12 −ia2ω12e−iθ12 2ia2ω12eiθ12 −2ia2ω12e−iθ12]T
dir. Benzer bir şekilde, ivme denklemi:
Aα = c
olup α = [α13 α14 α15 α16]T ve (ω12 sabit olduğu için α12 = 0)
c = \displaystyle \left[ {\begin{array}{c} {-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}}}}+{{\text{a}}_{3}}{{\text{ω}}_{{13}}}^{2}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}-{{\text{a}}_{4}}{{\text{ω}}_{{14}}}^{2}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}}}}} \\ {-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{12}}}}}}+{{\text{a}}_{3}}{{\text{ω}}_{{13}}}^{2}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}-{{\text{a}}_{4}}{{\text{ω}}_{{14}}}^{2}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}}}}} \\ {-2{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}}}}+{{\text{c}}_{3}}{{\text{ω}}_{{13}}}^{2}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}+{{\text{a}}_{5}}{{\text{ω}}_{{15}}}^{2}{{\text{e}}^{{\text{i}{{\text{θ}}_{{15}}}}}}-{{\text{a}}_{6}}{{\text{ω}}_{{16}}}^{2}{{\text{e}}^{{\text{i}{{\text{θ}}_{{16}}}}}}} \\ {-2{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{12}}}}}}+{{\text{c}}_{3}}{{\text{ω}}_{{13}}}^{2}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}+{{\text{a}}_{5}}{{\text{ω}}_{{15}}}^{2}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{15}}}}}}-{{\text{a}}_{6}}{{\text{ω}}_{{16}}}^{2}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{16}}}}}}} \end{array}} \right]
dır. Uzuvların açısal hız ve ivmeleri devre hız ve ivme denklemlerinden çözüldükten sonra F noktasının hız ve ivmesi A0F konum vektörünün birinci ve ikinci türevlerinin alınması ile belirlenir:
vF = ia2ω12eiθ12 + iω16eiθ16(a6 − b6eiζ)
aF = ia2ω122eiθ12 + iα16eiθ16(a6 − b6eiζ) − iω162eiθ16(a6 − b6eiζ)
Bu karmaşık denklemlerin her an reel ve sanal kısımları ayrı ayrı yazılması mümkündür. Ayrıca istenir ise, matris hız ve ivme denklemlerinin uzuvların açısal hız ve ivmelerine göre ayrı ayrı çözülmesi de mümkündür (Matris denklemleri incelendiğinde, ilk iki hız denkleminden ω13 ve ω14 doğrudan ω12 ye göre çözülebilir. Son iki hız denkleminden ise ω15 ve ω16, ω13 ve ω12 ye göre çözülebilir. Aynı durum açısal ivme için söz konusudur).
Tüm çevrim için hız ve ivmenin polar diyagramı aşağıda (a) ve (b) şekillerinde gösterilmiştir (× ile gösterilen nokta kol açısının 90° olduğu konumdur). Hız ve ivme mm/s ve mm/s2 olarak ölçülmüştür.
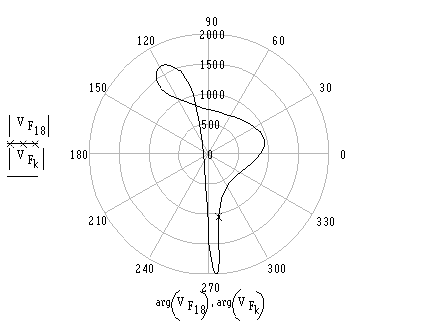
(a) Polar hız diyagramı
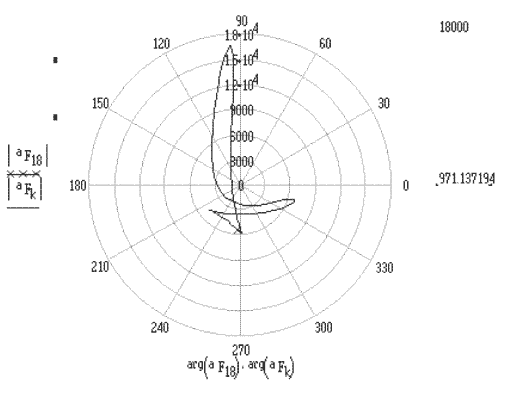
(b) Polar ivme diyagramı
Mekanizmanın konum analizi için hazırlanmış olan eksel kütüğü buradadır: –BalyalamaMek.xls-. Bu kütüğü kullanarak (isterseniz Sheet2 sayfasında, veya aynı sayfada) Balyalama mekanizmasının hız ve ivme analizini yapın ve polar hız ve ivme diyagramlarını çizin.
Kol açısının 90° olduğu verilen konumda grafik analiz yaptığımızda, 2 uzvu sabit bir hızda (ω12 = 4 rad/s) döndüğüne göre A ve B noktalarının merkezden uzaklığı ile açısal hız çarpılarak vA = vB = 728 mm/s olarak elde edilir. vA sola doğru iken, vB hız vektörü sağa doğru olacaktır. kv = 0.5 mm/(mm/s) olan bir ölçek kullanarak bu bilinen hız vektörlerini çizelim. 1, 2, 3 ve 4 uzuvlarından oluşan devre göz önüne alındığında bu devrenin türevinden elde edilecek olan hız devre denkleminin vektörel gösterimi:
vC = vB + vC/B
olarak yazılabilir. vC/B, CB doğrusuna dik ve vC, CC0 doğrusuna dik olacaktır. Verilen konumda BA0 ve CC0 paralel olduğundan, vC ve vB eşit olup vC/B = 0 ve ω13 = 0 olmalıdır. Bu durumda vD = vC = vB dir. Bundan sonra 5 ve 6 uzuvları üzerinde daima çakışan noktalar olan E noktasını göz önüne alalım. D ve E noktaları 5 uzvu üzerinde olduğuna göre:
vE = vD + vE/D
yazılabilir. Benzer bir şekilde A ve E noktaları 6 uzvu üzerinde olduğundan:
vE = vA + vE/A
yazılabilir. vD ve vA hız vektörlerinin şiddetleri ve yönleri biliniyor isede vE/D ve vE/A bağıl hız vektörlerinin yönlerinin sırası ile ED ve EA doğrularına dik oldukları söylenebilir. Bu iki vektör denklemi ayrı ayrı E noktasının hızını bulmak için yeterli değil isede her iki denklemin sağ tarafları birbirlerine eşitlendiğinde ilk olarak vE/D ve vE/A bağıl hız vektörlerinin şiddeti sonrada çakışma noktasından dolayı vE hız vektörü bulunur. F noktasının hızı için ise Mehmke teoremi kullanılabilir veya
vF = vE + vF/E
vF = vA + vF/A
denklemlerine ortak çözüm yapılır. Sonuç aşağıda görüldüğü gibidir.
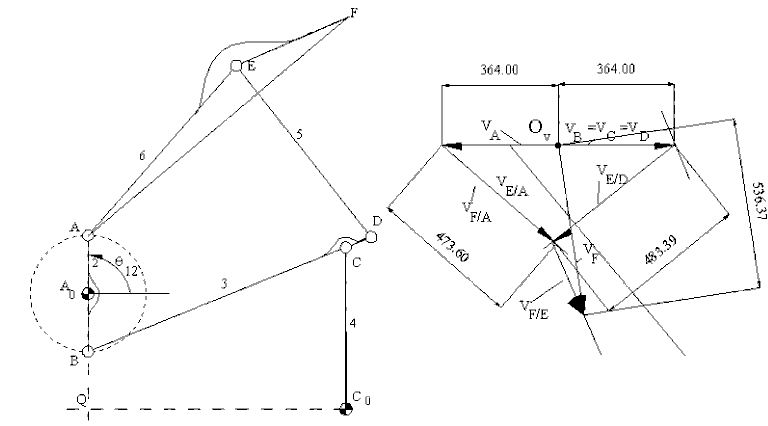
Grafik hız analizi
İvme analizi için ise, hız analizinda kullandığımız noktalar aynen kullanılmalı, ancak bu noktaların ivmeleri normal ve teğetsel ivmeler olarak bileşkeleri kullanılarak yazılmalıdır. 2 uzvu sabit bir hızda döndüğünden, A ve B noktalarının teğetsel ivmeleri yoktur. (aA = anA, aB = anB). Bu durumda her ikisi de dönme merkezine doğru olmak üzere A ve B noktalarının ivme şiddetleri aA = aB = 2912 mm/s2 olarak bulunur. ka = 0.2 mm/(mm/s2) olarak bir ölçek kullanarak bu vektörleri çizelim (üstteki şekil). Şimdi C noktasının ivmesini, B noktasının ivmesi ve bağıl ivme olarak yazalım:
anC + atC = anB + anC/B + atC/B
anC normal ivmesi CC0 yönünde C0 a doğru olup şiddeti: ω132|CC0| = vC2/|CC0| = 1045 mm/s2 dir. Bu konum için ω13 = 0 olduğundan anC/B = 0 olacaktır. atC ve atC/B sırası ile CC0 ve CB doğrularına diktir (şiddetleri bilinmemektedir). Bu doğruların ivme poligonunda çizilerek çakışma noktalarının belirlenmesi bilinmeyen atC ve atC/B ivme şiddetlerini verir. Dikkat edilir ise ω13 = 0 olması açısal ivmenin sıfır olmasını gerektirmeyecektir. Yani α13 ≠ 0. atD/B bulunabilir (α13 = atC/B/|CB| açısal ivme bulunur ve atD/B = α13|DB| dir). ω13 = 0 olduğundan anD/B = 0 olacaktır. Böylece aD ivmesi bulunur . E noktası için hız analizinde olduğu gibi:
aE = aD + anE/D + atE/D
ve
aE = aA + anE/A + atE/A
yazılabilir.
anE/D = ω152|ED|= vE/D2/|ED| = 1366 mm/s2 (ED yönünde D ye doğru)
anE/A = ω162|EA| = vE/A2/|EA| = 1269 mm/s2 (EA yönünde A ya doğru)
Teğetsel ivme bileşenleri atE/D ve atE/A sırası ile ED ve EA doğrularına diktir (şiddetleri bilinmemektedir). Her iki denklem için ortak çözüm yapılarak önce bu bağıl teğetsel ivmelerin şiddeti bulunur ve sonra vektörel toplamla E noktasının ivmesi belirlenir. F noktasının ivmesini bulmak için ise Mehmke teoreminden yararlanılabilir (ivme poligonunda aef üçgeni, mekanizmada 6 uzvu üzerinde AEF üçgeni ile benzerdir). Sonuç şekilde görülmektedir. Sayısal olarak aF = 1075.5/0.2 = 5378 mm/s2 aşağıya doğru elde edilmiştir.
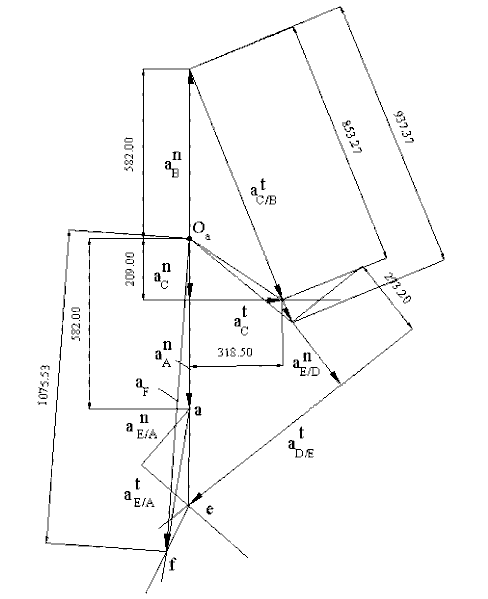
İvme analizi
Mekanizmanın AutoCad kütüğü: –SamanBalyalama.dwg–