Mekanizma Serbestlik Derecesi ve Mekanizmaların Sınıflandırılması

1.4 Degree of Freedom of Mechanisms -1

The degree of freedom of a mechanism is the number of independent parameters required to define the position of every link in that mechanism.

As an example consider a very simple mechanism with four links connected to each other by four revolute joints.

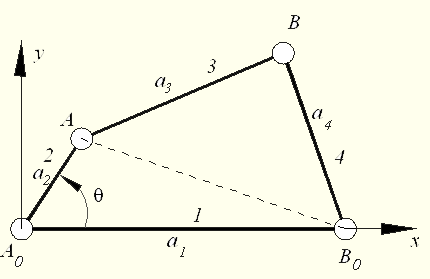Assuming that the link lengths are known, if the value of the angle is given, then the position of every link can be determined by determining the coordinates of two points on each link. (A₀B₀ (Link 1 ), A₀A (Link 2), AB (Link 3) ve BB₀ (Link 4)). This is due to the fact that when is given the triangle A₀B₀A is known (Side-Angle-Side) and the distance AB₀can be calculated. Next, the triangle ABB₀ is known completely (side-Side-Side). We only need one parameter to locate the position of every link. For a Four-Bar mechanism, the degree of freedom of the mechanism is 1. .

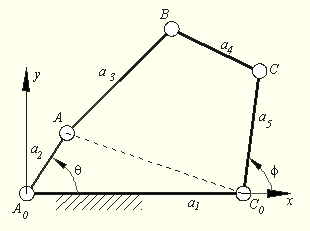Consider a mechanism with five links connected to each other by five revolute joints as a second example. If the angle is defined we can solve for the triangle A₀AC₀. However, the remaining links is a quadrilateral (ABCC₀) which will require an additional parameter (Such as angle ) to locate the links. In such a case, since the number of parameters required to determine the position of the links is 2, the degree of freedom of this five link mechanism is 2.

In the above examples:

1. Instead of the angles and, other angles can be used as a free parameter. But in every case, for a particular mechanism the number of parameters required is unique. For example in the first example the angle BB₀ makes with the horizontal can be selected as a free parameter and the position of each link will be uniquely determined.

2. The number of parameters required is not a function of the link lengths. For example if the length a₂ is 5 units instead of 4, the degree of freedom of the four-bar mechanism is 1 and of five-link mechanism is still 2.

Conclusion:

The degree of freedom of a mechanism does not depend on the link lengths. It depends on the number of links, number of joints, the type of joints and their distribution within the mechanism.