6.2.2. Principle of Superposition
In the previous examples, there was only one known external force acting on one member of the mechanism and the system was brought to static equilibrium by an input or output force (or torque). The magnitude of this force or torque was an unknown. If there are two or more known external forces acting on one link, these forces can be combined into a single resultant and the problem reduces to the case we have already discussed. However, in real machinery there are several external forces acting on different links. For example, if we do not neglect the weight of the members, there will be at least one known external force on each link. In such a case, if we draw the free body diagrams of the links, no simplification will be possible and one has to write three equilibrium equations for each link. The resulting 3(l-1) linear equations will include 3(l-1) unknown joint force components and the input force (or torque). Usually simultaneous solution of the equilibrium equations would be required.. Another solution method the principal of superposition. This principal states that the effect of the forces is the sum of the individual effects of the forces considered separately. In other words, if there are two or more external forces present, one can neglect all but one of the forces and determine the joint forces and the unknown reaction force that brings the system into equilibrium for this one external force. If the above procedure is carried out for each of the external forces, at each joint there will be different joint forces corresponding to each external force. The resultant joint force is the vectorial sum of all these forces. We shall explain this by solving the same problem by (a) without using the principal of superposition and b) by using the Principal of superposition.
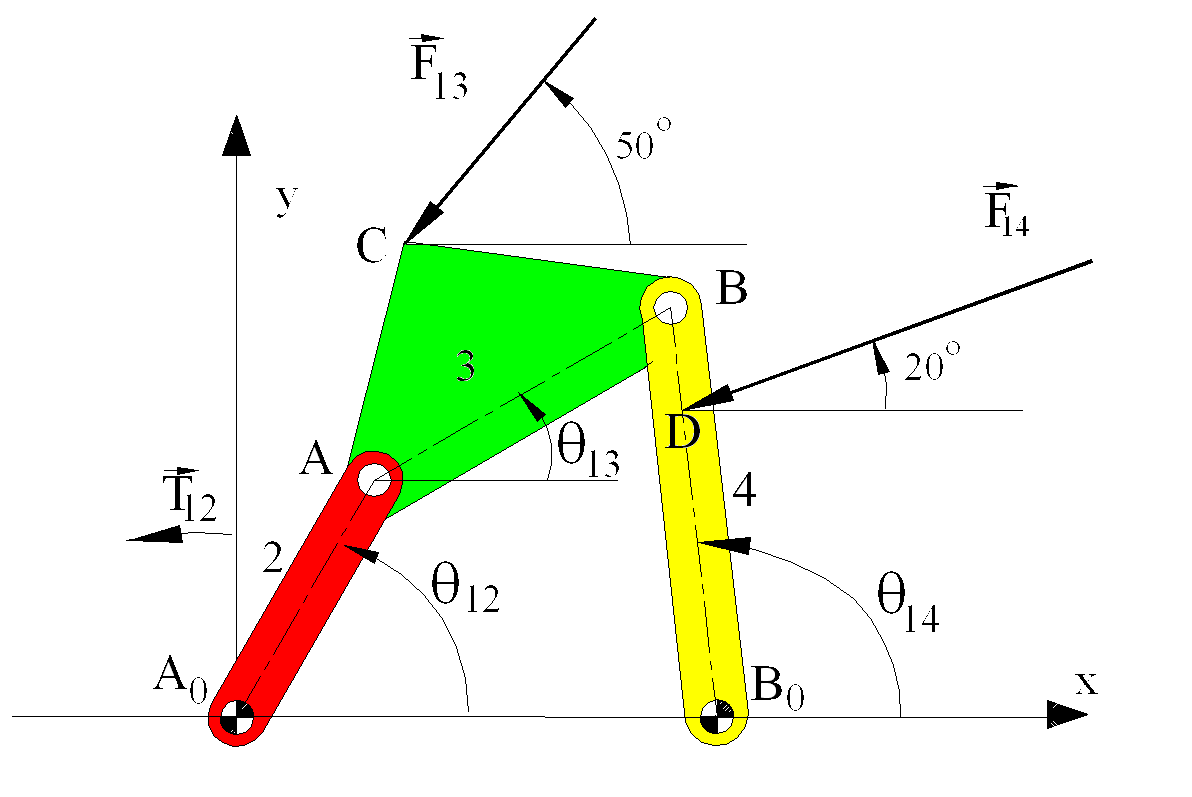
Example 6.3.

For the mechanism shown A0A= a2= 80, AB= a3 =100, B0B= a4=120, A0B0= a1= 140, AC= b3 = 70, BC=80 and B0D= b4=90 mm. When q12=600, from kinematic analysis q13=29,980 , q14 = 96.400. Two forces F13=50 N < 2300 and F14= 100 N < 2000 are acting on links 3 and 4 respectively.
Solution without the principal of superposition
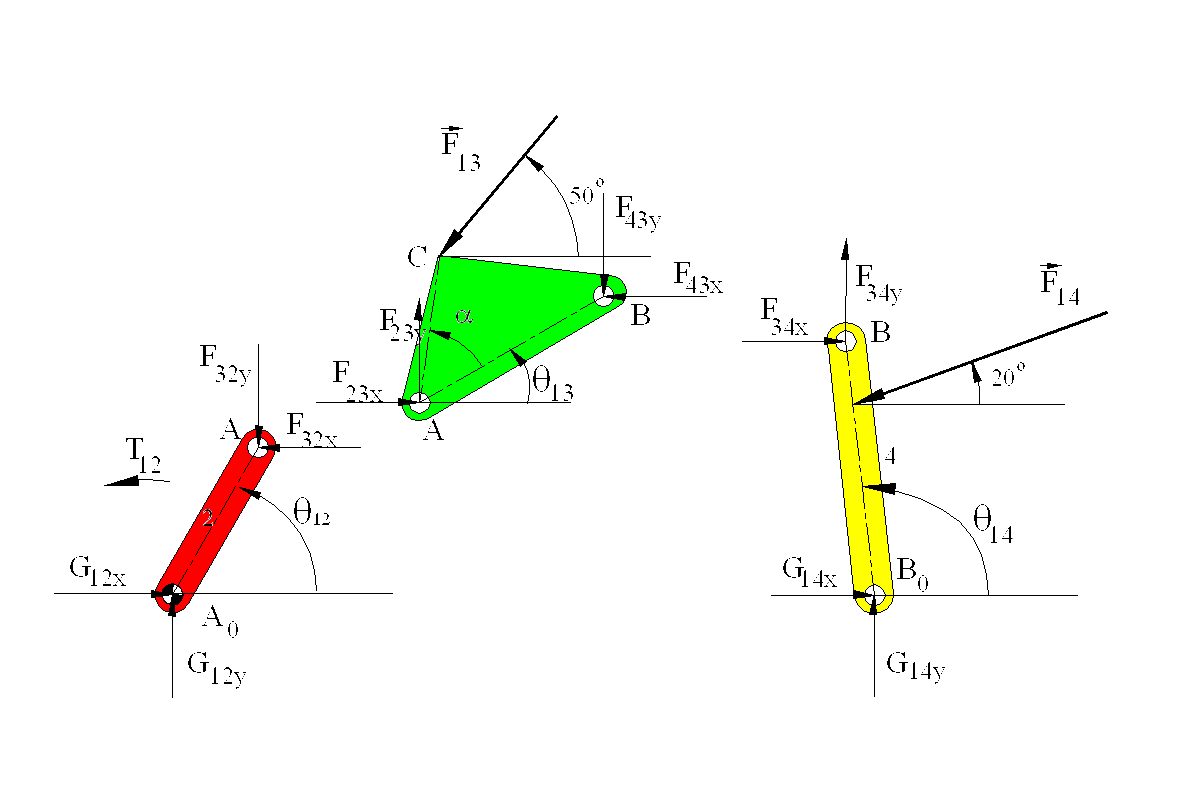
The free-body diagrams of the moving links are shown .
The three equilibrium equations for link 4 are:
|
There are four unknowns in three equations, therefore the equations obtained from one free-body diagram is not enough to solve for the unknowns. Equations 1 and 2 can be used to solve for G14x and G14y , only when F34xy and F34y are determined. The three equilibrium equations for link 3 must also be written (note that F34 and F43 are of equal magnitude).
| F23x - F34x - F13cos(500) = 0 | (SFx= 0) | (4) |
| F23y - F34y -F13sin(500) = 0 | (SFy= 0) | (5) |
| -F34x a4 sinq14 + F34ya4 cosq14 - F14 b4 sin(200-q14 ) =0 | (SMA= 0) | (6) |
Where a= 52.620 (using the cosine theorem for the triangle ABC).
Equations 4 and 5 can be used to determine F23x and F237x. Equations 3 and 6 must be used simultaneously to solve for F34x and F34y. Substituting the known values into equations 3 and 6 results:
| -119.25 F34x - 13.38 F34y + 8748 =0 | (3) |
| 49.97 F34x - 86.62 F34y + 1886= 0 | (6) |
Simultaneous solution of the two equations yield:
F34x = 66.60 N F34y = 60.20 F34 = 89.78 N < 42.110
From equations 1 and 2:
G14x = 27.37 N G14y = 26.00 N G14 = 37.75 N < -43.530
From Equations (4) and (5):
F23x = 98.74 N F23y = 98.50 N F23 = 139.46 N < 44.930
Now, link 2 can be treated as a two force and a moment member (G12=-F32=F23). The moment equilibrium (about A0):
T12 -F23a2 sin(47.340-600) =0 or T12 = -2908 N-mm (2.9 N-m CW)
Solution Using the pricipal of superposition

The same problem will be solved usiing the principle of superposition. Let us consider two problems:
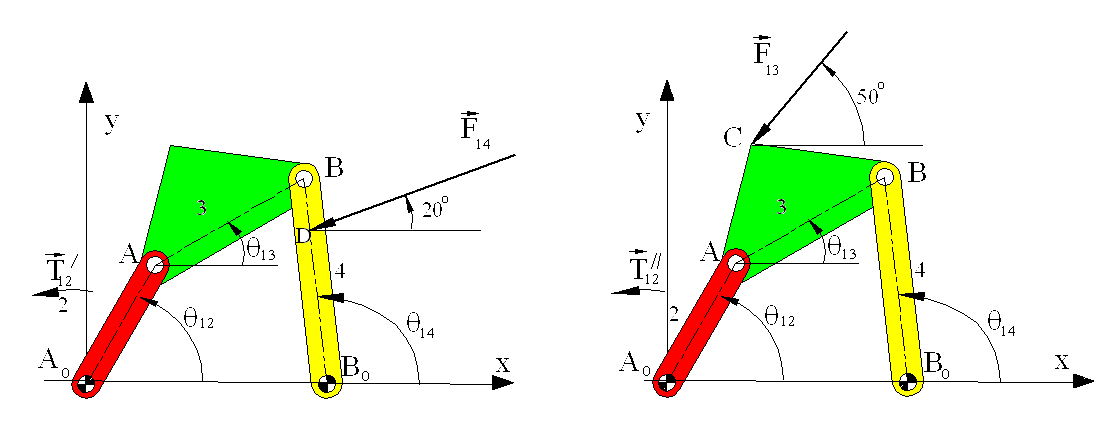
(a) (b)
In problem (a) The mechanism is under the action of F14 and in (b) F13 only. . If we denote the joint forces due to F14 by a single prime and the forces due to F13 by double prime, we have the free-body diagrams due to F14 as shown:
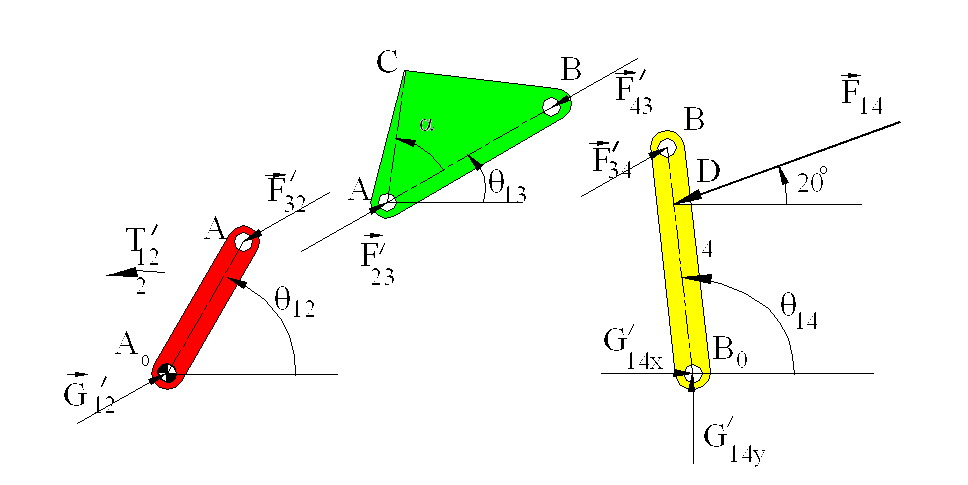
Due to F14, the moment equilibrium for link 4 yields:
F34’a4sin (q13-q14)-F14b4sin (200-q14)=0
from which F34'= 79.54 N < 29.980 (=q13).
Since F34'= - F43' = F23' = - F32' = G12’ (links 3 and 2 are two-force and two force and a moment members respectively ; also action-reaction between bodies 2,3,4), we have to write the moment equilibrium for link 2 only:
T12'- F32' a2sin((q13-q12) = 0
from which T12'= -3184 N-mm = 3.18 N-m CW.
.Due to F13 only:
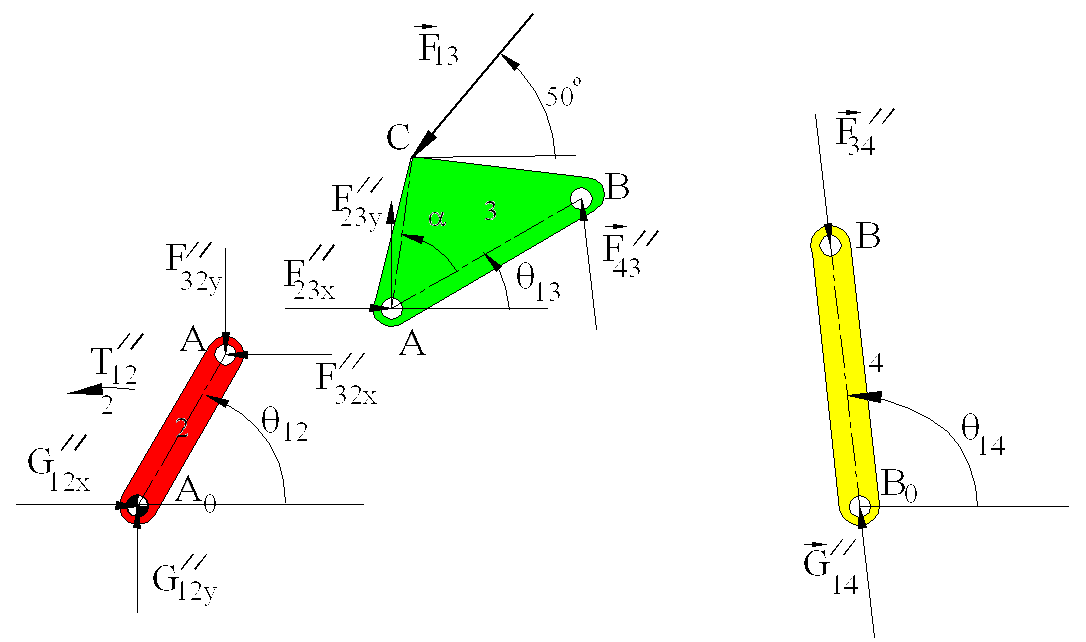
link 4 is a two-force member, link 3 is a three force member while link 2 is a two-force and a moment member as before.
The moment equilibrium equation for link 3 yields:
F43"a3sin(q14-q13)-F13b3sin(500-q13)=0
from which F43"= -20.57 N < 96.400 (=q14) or F34"= -F43"= 20.57 N < 96.400
F23x" and F23y" can be determined using the force equilibrium equations for link 3:
F23x"= F13 cos500 + F43"cos(q14) = 29.85 N
F23y"= F13 sin500 + F43"sin((q14)) = 58.74 N
F23" = 65.89 N < 63.060
Now, the moment equilibrium for link 2 yields:
T12"- F32" a2sin(63.060-q12) = 0
from which: T12"= 282 N-mm (.28 N-m CCW)
One can now superimpose the two solutions. For example, the torque T12 required for the original system will be:
T12 = T12'+ T12" = -3184 +282 = -2902 N-mm (2.9 N-m CW)
Similarly:
F34x = F34x' + F34x" = 79.54 cos(29.980)+ 20.57cos(96.400) = 66.60 N
F34y = F34y' + F34y" = 79.54 sin(29.980)+ 20.57sin(96.400) = 60.19 N
F23x = F23x' + F23x" = 79.54 cos(29.980)+ 29.85 = 98.75 N
F23y = F23y' + F23y" = 79.54 sin(29.980)+ 58.74 = 98.49 N
F23 = G12= 139.5 N < 44.920
F34= 89.77 N < 42.110
The results are in good agreement with the results obtained previously (differences are due to the round-off errors)