3.8 Devre Kapalılık Denklemlerinin Sayısal Çözümü
Elde etmiş olduğumuz denklemler ve benzer yöntemlerle başka mekanizmalar için elde edeceğimiz denklemler bir mekanizmanın her hangi bir konumunu veya mekanizmanın olası tüm konumlarını belirlememizi sağlar. Bunun için uzuv boyutları bilindiğinde bu denklemlerin sayısal olarak çözülmesi gereklidir. Mühendislikte analitik çalışmalar sonucunda elde edilenler sayısal değerlere dönüştürülmeden yapılanların uygulamaya indirilebilmesi mümkün değildir.
Mekanizmaların sayısal çözümü uzun yıllar çizim masasında pergel ve cetvel kullanılarak geometrik yöntemlerle yapılmıştır. Bu yöntemin olumlu yanı kişinin yapmakta olduğu işi çok iyi canlandırmasına olanak tanımasıdır. Benzer geometrik çözüm bilgisayarlarda günümüzde AUTOCAD®, CADKEY® ve benzeri çizim programları kullanılarak yapılabilir. Geometrik yöntem açıklanırken bu tür çözümün örnekleri verilmiştir. Ancak geometrik yöntemler çok zaman aldığı gibi, hassasiyetleri sınırlı olup uygulayan kişinin becerilerine çok bağlı olduğundan mühendislikte sayısal çözüme daima ihtiyaç duyulmuştur.
Bilgisayarların uygulamaya girdiği ilk yıllarda mekanizmaların bilgisayar destekli analizi ve sentezi söz konusu olmuştur. 1950'li yıllardan itibaren ilk olarak elde edilmiş olan analitik denklemler ve algoritma FORTRAN programlama dili ile bilgisayarlara uyarlanmıştır. Bilgisayarlar teknolojisinde gelişmelerle birlikte BASIC, PASCAL ve C lisanlarıda bu algoritmaların bilgisayarlarda uyarlanmasında kullanılmıştır. Bu uygulamaların sonucu ne yazıkki görsel açıdan çok zayıf olup genellikle çok sayıda rakamlardan oluşan uzun bilgisayar çıktıları olmuşdur. Bu nedenle işin uzmanları tarafından çok özel uygulamalar için kullanılabilmiştir. Bu bilgisayar lisanlarına günümüzde grafik komutlar kazandırılmış olmalarına rağmen, genellikle grafik uygulamalar için grafik özellikleri daha uygun ve kullanıcı ile etkileşimli program yazılmasına uygun olanaklar ve ortam oluşturabilen VisualBasic, VisualC++ ve Delphi gibi program yazma platformları geliştirilmiştir.
Kişisel bilgisayarlarla birlikte bilgisayar kullanımının daha yaygınlaşabilmesi için kullanıcılara öğrenilmesi programlama dillerinden nisbeten daha kolay, genel amaçlı kullanıcı ile iletişimli paket programlar geliştirilmiştir. En yaygın olan paket programlar bilgisayarın bir yazıcı olarak çalışmasını sağlayan paket programlardır. Daktilodan çok daha farklı olarak, değişik yazı karakterleri ve boyutları kullanmamıza olanak tanıyan, satır sonlarını düzenleyen bu paket programlar günümüzde daktilolardan daha fazla kullanılmaktadır. İkinci yaygın paket program ise, çarşaf liste hazırlamak için kullanılan programlardır. Bu programlar ilk olarak muhasebe işlemlerini kolaylaştırmak için düşünülmüştür. Örneğin masrafları gösteren bir kolondaki sayılar kolayca toplanabilir veya maliyeti gösteren bir kolon belirli bir genel gider yüzdesi ile çarpıldıktan sonra elde edilmesi hedeflenen yüzde kar ile çarpılarak bir başka kolona satış fiyatı kolonu olarak elde edilmesi açısından bu tür liste programları çok kullanılışlı olmuştur. Ancak zamanla basit çarpma, bölme toplama gibi hesaplamalardan çok daha fazla fonksiyonları (her türlü istatistik işlemleri, trigonometrik fonksiyonları) içerir hale getirilen bu programlar günümüzde mühendisler için her türlü analizi yapabilecek, sonucu grafik olarak gösterebilecek vazgeçilemiyen bir paket olmuştur. Günümüzde Microsoft Excel®, Lotus 123® ve Corel Quattro Pro® değişik firmalar tarafından üretilen üç önemli çarşaf listeleme paket programlarıdır. Günümüzde bu paket programların çok yaygın olarak bilgisayarlarda olması, bu paket programların her mühendis tarafından öğrenilmesini gerekli kılmaktadır.
Bilgisayar alanında gelişmelerle birlikte mühendislik, matematik ve fen bilimlerinde uğraşan kişiler için son yıllarda her türlü matematiksel işlemi yapabilecek matematik uygulama programlarının geliştirilmesidir. Maple®, Mathematica®, MATLAB®, Mathcad®, SCILAB®, TKsolver®, Eureka® bunlardan önemli olanlardır.
Mekanizmaların kinematik ve dinamik analizi için ayrıca özel paket programlar geliştirilmiştir (ADAMS®, WorkingModel®, vb ).. Bu paket programlar kullanılarak düzlemsel veya uzaysal mekanizmaların kinematik ve dinamik analizi mümkündür. Ancak konunun temeli öğrenilirken bu paket programların kullanılması sakıncalı olacaktır. Konunun uzmanı olunduktan sonra bu programlar zaman kazandırdığından dolayı kullanılabilir.
Analizi yapılabilecek mekanizmaların burada vereceğimiz örneklerle sınırlı olması düşünülemez. Ayrıca her geçen gün farklı çözüm imkanlarının ortaya çıktığıda bir gerçektir. Ancak temel matematiksel yaklaşımlar mekanizmaların temel geometrilerine bağlı kaldığından, değişmesi beklenmemelidir.
Burada amaç bilgisayar programlamayı öğretmek veya bir paket programı kullanmayı öğretmek olmadığından anlatılacak olan daha çok söz konusu mekanizma analizinin bilgisayarlarda sayısal yöntemlerle en kolay bir şekilde nasıl yapılacağını açıklamaktır. Bunun için Excel ve Mathcad paket programları kullanılarak yapılan çözüm örnekleri verilecektir. Kullanılacak olan denklemler ve algoritma aynı olacağından açıklanmış olan yöntem kolaylıkla başka bir paket program kullanarak veya bir bilgisayar lisanı kullanılarak o problem için özel bir program yazılarak çözülebilir. Bilgisayar kullanmayı çok iyi bilenler, burada analtılanlardan çok daha fazlasını daha güzel bir görünüm verecek şekilde yapılabileceğini kolaylıkla söyleyebilirler.
Örnek

Gösterilen krank-biyel mekanizmasında uzuv boyutları:
a2= 50 mm; a3=
250 mm; b3=120 mm; a1=
20 mm and ![]() 3
= 30o
3
= 30o
C noktasının koordinatlarını ![]() 12=
60o iken bulun.
12=
60o iken bulun.
Krank Biyel mekanizması için elde ettiğimiz denklemler yeniden yazıldığında:
 |
verilmiş olan sayısal değerler kullanıldığında:
Çözüm ![]() 13=5.3o
veya 174.7o olacaktır. Şekil göz önüne
alındığında
13=5.3o
veya 174.7o olacaktır. Şekil göz önüne
alındığında ![]() 13=174.7o.
olacağı açıktır. Bundan sonra s14:
13=174.7o.
olacağı açıktır. Bundan sonra s14:
|
s14= a2
cos s14= 50 cos 60o - 250 cos 174.6o = 273.9 mm |
C noktasının konum vektörü A0C = A0B + BC olarak yazılır, x ve y bileşenleri ayrı ayrı ele alınır ise:
|
xc= x + b3
cos( xc= 273.9 + 120 cos(174.7o - 30o) = 176.0 mm yc= a1
+ b3 sin( yc= 20 + 120 sin(174.7o - 30o) = 89.4mm |
Hesap makinası programlanabilir ise, bir defa yapılan bu işlemler makina
hafızasına alınarak değişik ![]() 12
açısına göre çözüm yapılabilir. Eğer işlemler hafızaya yerleştirilemez
ise, benzer hesaplama her açı için yeniden tuşlanarak yapılmalıdır.
12
açısına göre çözüm yapılabilir. Eğer işlemler hafızaya yerleştirilemez
ise, benzer hesaplama her açı için yeniden tuşlanarak yapılmalıdır.
Örnek
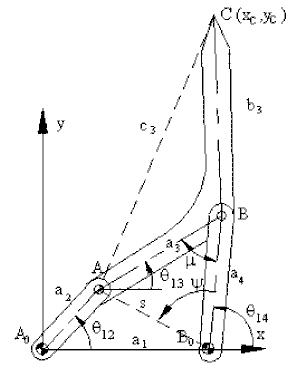
Yukarıda gösterilen dört-çubuk mekanizmasında uzuv boyutları:
a1=70 mm; a2= 35 mm; a3= 62.3 mm; a4= 56 mm; BC= c3 = 84.1 mm; AC=b3=126.6 mm dir.
0o< ![]() 12<360o
aralığında ve her 5o de
12<360o
aralığında ve her 5o de ![]() 13
ve
13
ve ![]() 14
konum değişkeni değerlerini ve C noktasının koordinatlarını bulmak istiyoruz.
Bilinmeyen Konum değişkenlerini bağımsız değişkene göre bulmak için gereken
denklemler, önceden elde edildiği gibi:
14
konum değişkeni değerlerini ve C noktasının koordinatlarını bulmak istiyoruz.
Bilinmeyen Konum değişkenlerini bağımsız değişkene göre bulmak için gereken
denklemler, önceden elde edildiği gibi:
|
xa = scos ya = ssin
xc = xa
+ a1 + b3
cos( yc = ya
+ b3 sin( |
Bu denklemde ![]() sabit
sabit ![]() ABC
açısı olup, verilen uzuv boyutlarına göre kosinüs teoremi kullanılarak
bulunabilir:
ABC
açısı olup, verilen uzuv boyutlarına göre kosinüs teoremi kullanılarak
bulunabilir:
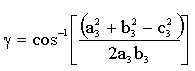 |
Bu örneği EXCEL® paket programını kullanarak çözelim. Excel bir genel tablolama programıdır. Genel olarak tablolama programlarında çok sayıda hücreler bulunmaktadır. Hücreler rakamla belirtilen yatay satırlar ve harflerle gösterilen dikey kolonlar üzerinde bulunduğundan her hangi bir hücre kolon harfi ve satır rakamı ile gösterilir. Yani her bir hücrenin bir adı vardır. C25 (C kolonunda, 25inci satırda bulunan hücre ), A1 (birinci satır birinci kolon) AH55… gibi. Bir hücrenin adını isterseniz sizde etiketleme yaparak değiştirebilirsiniz. Bu hücreleri içine her hangi bir rakam, veya isim yerleştirebiliriz. Bu şekilde isterseniz güzel görünümlü tablolar veya listeler oluşturabiliriz. Bu tür paket programların mühendislik açısından en önemli avantajı, her türlü matematiksel kuralları kullanarak hücrelere yazılmış olan rakamlar üzerinde gerekli işlemlerin yapabilmesidir. Basit dört işlemin yanında bu programlarda her türlü trigonemetrik fonksiyon, istatistik fonksiyonları (maksimum, minimum, ortalama bulma,…) ve benzer fonksiyonlar bulunduğu gibi matris inversi alınması, matris çarpımı veya bir lineer olmayan denklemin köklerinin bulunması dahil olmak üzere çeşitli işlemler basit komutlarla yapılabilir. Gerektiğinde paket programda bulunmayan ancak kullanıcının devamlı kullanacağı fonksiyonlar ise MACRO olarak adlandırılan işlem ile veya VISUAL BASIC lisanı kullanarak yazılıp eklenebilir ve kullanılabilecek fonksi-yon sayısı artırabilir. Örneğin bir hücredeki sayının karesini alıp diğer bir hücredeki sayının kosinüsü ile çarpıp bir başka hücreye bu değerin kare kökünü yazdırabilirsiniz. Bu özellikler mekanizmaların analizi için yeterlidir.

Sabit uzuv boyutları a1, a2,
a3, a4
değerlerini A1 den A4 e kadar olan hücrelere yerleştirelim. A7 hücresine
![]() 12
açısının ilk değeri olan (0.00) ı yerleştirelim. Şimdi A7 hücresindeki
sayıyı
12
açısının ilk değeri olan (0.00) ı yerleştirelim. Şimdi A7 hücresindeki
sayıyı ![]() /180
ile çarparak
/180
ile çarparak ![]() 12
açısını radyana çevirip B7 hücresine sonucu yazalım. Bunun için B7 hücresine
girip =A7*PI()/180 ı tuşlamamız veya B7 hücresine gelip Excel'in
dereceden radyana dönüşüm fonksiyonu olan =RADIANS(A7) yazmamız
gerekir (Excel trigonemetrik fonksiyonlarında
açılar radyan olmalıdır). Dikkat edilir ise, bir işlem tanımlanırken
ilk olarak "=" işaretinin veya + - işaretlerinden
birinin kullanılması gerekir. Aksi takdirde bilgisayar yazılanları
o hücreye konulması gereken harfler olarak algılayacak, yapılması gereken
işlem olarak görmeyecektir. Bir fonksiyonu yazarken büyük veya küçük harf
fark etmeyecek, bilgisayar küçük harfleri büyük harfe otomatik olarak
çevirecektir. Ayrıca, fonksiyonları yazarken yazılım şeklini unuttuğumuz
veya hatırlamadığımız durumlarda programın yukarısında görülen Insert
menu listesine girip fonksiyon tuşuna basar isek mevcut fonksiyonları
görebiliriz. Benzer bir şekilde B7 hücresinden M7 hücresine kadar sıra
ile gerekli tüm işlemleri teker teker girebilir ara değerleri görebiliriz.
Girilmiş olan işlemler Excel sayfasının altıncı sırası olarak görülmektedir.
Hatırlamamız gereken önemli bir başka husus ise hücreler
arasında işlemler yukarıdan aşağıya ve soldan sağa doğru bir hiyerarşide
yapılacaktır. Normal olarak hücrelerde yapılması gereken ve
tuşladığımız işlemler görülmeyecek, sadece sonuç değer görülecektir. Bu
formüller doğru ve uygun bir şekilde girildi ise, A7 hücresindeki
12
açısını radyana çevirip B7 hücresine sonucu yazalım. Bunun için B7 hücresine
girip =A7*PI()/180 ı tuşlamamız veya B7 hücresine gelip Excel'in
dereceden radyana dönüşüm fonksiyonu olan =RADIANS(A7) yazmamız
gerekir (Excel trigonemetrik fonksiyonlarında
açılar radyan olmalıdır). Dikkat edilir ise, bir işlem tanımlanırken
ilk olarak "=" işaretinin veya + - işaretlerinden
birinin kullanılması gerekir. Aksi takdirde bilgisayar yazılanları
o hücreye konulması gereken harfler olarak algılayacak, yapılması gereken
işlem olarak görmeyecektir. Bir fonksiyonu yazarken büyük veya küçük harf
fark etmeyecek, bilgisayar küçük harfleri büyük harfe otomatik olarak
çevirecektir. Ayrıca, fonksiyonları yazarken yazılım şeklini unuttuğumuz
veya hatırlamadığımız durumlarda programın yukarısında görülen Insert
menu listesine girip fonksiyon tuşuna basar isek mevcut fonksiyonları
görebiliriz. Benzer bir şekilde B7 hücresinden M7 hücresine kadar sıra
ile gerekli tüm işlemleri teker teker girebilir ara değerleri görebiliriz.
Girilmiş olan işlemler Excel sayfasının altıncı sırası olarak görülmektedir.
Hatırlamamız gereken önemli bir başka husus ise hücreler
arasında işlemler yukarıdan aşağıya ve soldan sağa doğru bir hiyerarşide
yapılacaktır. Normal olarak hücrelerde yapılması gereken ve
tuşladığımız işlemler görülmeyecek, sadece sonuç değer görülecektir. Bu
formüller doğru ve uygun bir şekilde girildi ise, A7 hücresindeki ![]() 12
değeri farklı bir değerle değiştirildiğinde, girilmiş olan işlemlerde
bu hücreye yerleştirilmiş olan bu açı değeri kullanıldığından, tüm değerler
otomatik olarak değişecektir. Bu şekilde her
12
değeri farklı bir değerle değiştirildiğinde, girilmiş olan işlemlerde
bu hücreye yerleştirilmiş olan bu açı değeri kullanıldığından, tüm değerler
otomatik olarak değişecektir. Bu şekilde her ![]() 12
değeri için
12
değeri için ![]() 13,
13,
![]() 14
değerleri ve C noktasının koordinatları bulunabilir (uzun hesaplamalarda
bu otomatik hesaplamayı kaldırmak ve istendiğinde bir tuş komutu ile yaptırmak
mümkündür).
14
değerleri ve C noktasının koordinatları bulunabilir (uzun hesaplamalarda
bu otomatik hesaplamayı kaldırmak ve istendiğinde bir tuş komutu ile yaptırmak
mümkündür).
Şimdi A8 hücresine farklı bir ![]() 12
değeri yerleştirelim. Edit menusunda bulunan COPY (KOPYA) ve PASTE
(YAPIŞTIR) komutlarını kullanarak B7 den M7 ye kadar hücreleri B8 den
M8 e kadar hücrelere kopyalayalım.Dikkat edilir ise, işlemler kopyalanmıştır
ve eğer işlemlerde kullandığınız hücre sıra sayısı ve kolon harfinin başına
$ işareti koymadı iseniz, işlemlerde A7, B7...F7 olan hücreler işlem olarak
kopyalandığından A8, B8,...F8 olacaktır. Bu kopyalama işlemi sırasında
giriş açısına bağlı değerlerin değişmesini, ancak uzuv boyutu değerlerinin
her açı için sabit kalmasını sağlamamız gerekmektedir. Uzuv boyutunu içeren
hücreleri işlem içinde sabitlememiz için, örneğin a1 uzuv boyutu A1 hücresinde
olduğundan bu hücre işlemlerde yazılır iken $A$1 olarak yazılmalıdır (aksi
takdirde bir alt satıra işlem kopyalandığında A1, A2 olacağından işlemde
a1 boyutu yerine a2
boyutu yer alacaktır ve yanlış olur. Excel de ayrıca hücrelere istediğiniz
bir ismi verme imkanınızda olduğundan isterseniz bu sabitleme işlemini
o hücreye isim vererekde yapabilirsiniz. Bu ileride gösterilecektir.)
Şimdi 15o aralıklarla 0o
dan 360o kadar değerleri A7 den başlayarak
A kolonuna yazalım (isterseniz 1o aralıklarla
yazabilir daha büyük bir tablo elde edebilirsiniz. Burada 15o
aralığın kullanılmasının tek nedeni tüm sonucu tek bir sayfada yazma gerekliliğinden
doğmuştur). Bu aritmetik seriyi yazmak için A7 ye 0 ve A8 e 15 sayılarını
girdikten sonra, ilk olarak imleç ile bu iki hücreyi işaretleyip, imleci
A8 hücresinin alt sağ köşesine getirelim (imleç "+" işaretine dönüşecektir).
Şimdi sol tuş basılı olarak faremizi aşağıya doğru A31 e kadar sürükleyip
bırakır isek A7 den A31 e kadar hücreler 15o
aralıklarla 0o dan 360o
ye kadar doldurulmuştur. Şimdi yedinci sıradaki tüm işlemleri COPY,
PASTE komutları ile tüm sıralara taşıyalım. (Bu işlem için B7 den
M7 ye kadar hücreler ilk olarak imleç ile işaretlenir ve M7 hücresinin
sağ alt köşesinde imleç "+" işaretine dönünce farenin sol tuşu basılarak
M31 e kadar çekilir ise kopyalama işlemi yapılabilir) Bu şekilde tüm bağımsız
parametre değerleri için konum değişken değerleri ve C noktasının koordinatları
elde edilmiştir. Yani, istenilen her hangi bir giriş açısı değeri için
veya giriş açısının alabileceği tüm değerler için mekanizmanın konum analizi
yapılmıştır.
12
değeri yerleştirelim. Edit menusunda bulunan COPY (KOPYA) ve PASTE
(YAPIŞTIR) komutlarını kullanarak B7 den M7 ye kadar hücreleri B8 den
M8 e kadar hücrelere kopyalayalım.Dikkat edilir ise, işlemler kopyalanmıştır
ve eğer işlemlerde kullandığınız hücre sıra sayısı ve kolon harfinin başına
$ işareti koymadı iseniz, işlemlerde A7, B7...F7 olan hücreler işlem olarak
kopyalandığından A8, B8,...F8 olacaktır. Bu kopyalama işlemi sırasında
giriş açısına bağlı değerlerin değişmesini, ancak uzuv boyutu değerlerinin
her açı için sabit kalmasını sağlamamız gerekmektedir. Uzuv boyutunu içeren
hücreleri işlem içinde sabitlememiz için, örneğin a1 uzuv boyutu A1 hücresinde
olduğundan bu hücre işlemlerde yazılır iken $A$1 olarak yazılmalıdır (aksi
takdirde bir alt satıra işlem kopyalandığında A1, A2 olacağından işlemde
a1 boyutu yerine a2
boyutu yer alacaktır ve yanlış olur. Excel de ayrıca hücrelere istediğiniz
bir ismi verme imkanınızda olduğundan isterseniz bu sabitleme işlemini
o hücreye isim vererekde yapabilirsiniz. Bu ileride gösterilecektir.)
Şimdi 15o aralıklarla 0o
dan 360o kadar değerleri A7 den başlayarak
A kolonuna yazalım (isterseniz 1o aralıklarla
yazabilir daha büyük bir tablo elde edebilirsiniz. Burada 15o
aralığın kullanılmasının tek nedeni tüm sonucu tek bir sayfada yazma gerekliliğinden
doğmuştur). Bu aritmetik seriyi yazmak için A7 ye 0 ve A8 e 15 sayılarını
girdikten sonra, ilk olarak imleç ile bu iki hücreyi işaretleyip, imleci
A8 hücresinin alt sağ köşesine getirelim (imleç "+" işaretine dönüşecektir).
Şimdi sol tuş basılı olarak faremizi aşağıya doğru A31 e kadar sürükleyip
bırakır isek A7 den A31 e kadar hücreler 15o
aralıklarla 0o dan 360o
ye kadar doldurulmuştur. Şimdi yedinci sıradaki tüm işlemleri COPY,
PASTE komutları ile tüm sıralara taşıyalım. (Bu işlem için B7 den
M7 ye kadar hücreler ilk olarak imleç ile işaretlenir ve M7 hücresinin
sağ alt köşesinde imleç "+" işaretine dönünce farenin sol tuşu basılarak
M31 e kadar çekilir ise kopyalama işlemi yapılabilir) Bu şekilde tüm bağımsız
parametre değerleri için konum değişken değerleri ve C noktasının koordinatları
elde edilmiştir. Yani, istenilen her hangi bir giriş açısı değeri için
veya giriş açısının alabileceği tüm değerler için mekanizmanın konum analizi
yapılmıştır.
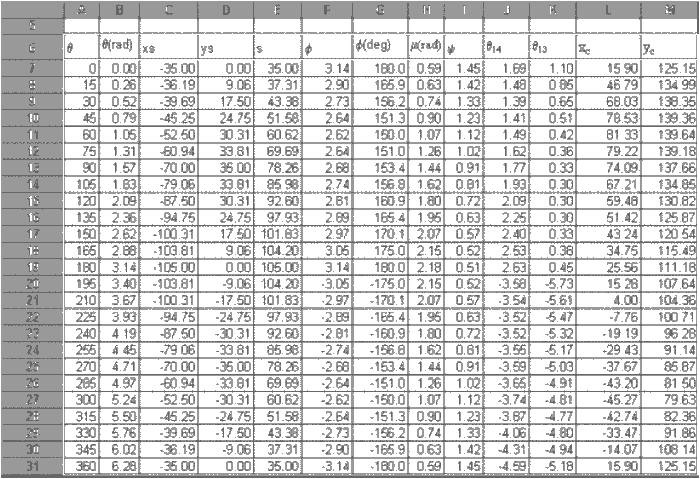
Sonuç değerler kolonlar şeklinde elde edildi ise de, bu değerlerin anlaşılması
oldukça zor olabilir. Hareketi gözlemliyebilmek için Excel paket programının
Chart menusunda bulunan grafik çizme özellikleri kullanılabilir. Aşağıda,
Excel paket programının bu özellikleri kullanılarak bağımlı konum değişkenleri
![]() 13,
13,
![]() 14
açıları ile kinematik açıdan önemli olan m açısının giriş kolu açısına
göre değişimi, ve C biyel noktasının yörüngesi grafik olarak gösterilmiştir.
(Bu şekilde x ve y eksen ölçekleri farklı olur ise eğri yanıltıcı olabilir).
14
açıları ile kinematik açıdan önemli olan m açısının giriş kolu açısına
göre değişimi, ve C biyel noktasının yörüngesi grafik olarak gösterilmiştir.
(Bu şekilde x ve y eksen ölçekleri farklı olur ise eğri yanıltıcı olabilir).
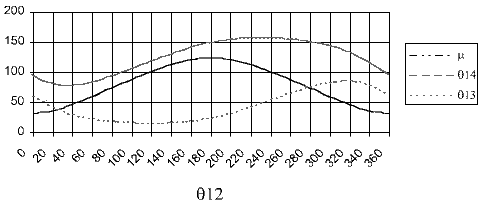
Krank Açısını göre çıkış kolu, biyel ve bağlama açıları

C biyel noktası eğrisi
Sayfamızda yapmak istediğimiz işlemler girildikten sonra çok önemli ve farklı bir konuya girme imkanımızda olacaktır. Mekanizmanın analizi için baştan verildiğini kabul ettiğimiz uzuv boyutlarını sorgulamamız mümkün olacaktır. Örnek olarak 70 mm olarak verilmiş olan a1 boyutunu ele alırsak, acaba bu boyut 65 mm veya 60 mm olur ise sonuçları nasıl etkiler diye bir araştırmaya girilebilecektir. Benzer sorgulama her uzuv için yapılabilir ve sonuç bütün farklı değerler için anında Excel sayfamızda hesaplanarak görülecektir ve grafikler yeni duruma göre anında değişecektir.
Yukarıda gösterilen işlemlerin Excel kütüğü için (four-bar.xls) tıklayınız.
 yukarıda verilmekte
olan kütük, kullandığınız internet programı içinde açılabilir ve excel
komutlarını kullanamıyabilirsiniz. Bu durumda mavi yazı üzerinde iken
sağ tuşa basıp çıkan menu dan "save target as" komutunu kullanarak *xls
kütüğünü diskinizde uygun bir yere uygun bir isimle kopyaladıktan sonra
bilgisayarınızda excel programını çalıştırıp "open" komutu ile bu
kütüğü açabilirsiniz.
yukarıda verilmekte
olan kütük, kullandığınız internet programı içinde açılabilir ve excel
komutlarını kullanamıyabilirsiniz. Bu durumda mavi yazı üzerinde iken
sağ tuşa basıp çıkan menu dan "save target as" komutunu kullanarak *xls
kütüğünü diskinizde uygun bir yere uygun bir isimle kopyaladıktan sonra
bilgisayarınızda excel programını çalıştırıp "open" komutu ile bu
kütüğü açabilirsiniz.
Bu tür paket programlarda eğer giriş parametresine göre diğer değerleri elde etmek için uygun ve doğru bir algoritma geliştirmiş isek, her hangi bir formülasyon yöntemini kullanabiliriz.
Örnek

Şekilde gösterilmiş olan mekanizma iki mekanizmanın seri bağlantısı olarak düşünülebilir. Birinci mekanizma (A0AB0, 1,2 ve 3 uzuvları), salınan kol-kızak mekanizması olup 2 krankının dönmesi ile 3 kolu salınım yapacaktır. İkinci mekanizma ise bir dört-çubuk mekanizması olup(B0BCC0 , 1,3,4 ve 5 uzuvları) 3 giriş uzvunun salınımı, 5 uzvunda farklı bir salınıma dönüşecektir. Önceden görüldüğü gibi, uygulamada mekanizmalar çoğunlukla belirli basit mekanizmaların seri bağlantısı olup bir basit mekanizmanın çıkış uzvu diğer mekanizmanın çıkış uzvu olmaktadır. Temel olarak karşılaşacağımız basit mekanizmalar dört-çubuk, kol-kızak, krank-biyel mekanizmalarıdır. Bu basit mekanizmaları tek bir fonksiyon kullanarak çözebilmek için Excel içinde program yazmamız ile mümkündür. Bunun için TOOLS menüsünden Macro seçilir ve VisualBasic Editörüne girilebilir ve VisualBasic programlama komutları kullanılarak Çeşitli fonksiyonlar ve alt programlar yazılabilir. Yazılan bu programlar "FILE- EXPORT"komutu ile diskte saklanabildiği gibi, başka bir Excel kütüğünde kullanmak istediğimizde "FILE - IMPORT" komutu ile çağırılabilir. Bu işlem basit mekanizmalar için bir defa hazırlanıp bir kütüphane oluşturulur ise, mekanizma analizi yazılmış olan bu fonksiyonlar ile bir iki komuta indirgenebilecektir.
- EK 2 için tıklayınız -
Ek 2 de Visual
Basic® ile hazırlanmış, Excel paket programı veya VisualBasic
programlama lisanı içinde kullanılabilecek temel bazı fonksiyonlar verilmektedir.
Bu örnekte verilmiş olan mekanizma için bu hazır programlar kullanılacaktır.
Bir önceki örnekten farklı olarak hücre adlarını kolon harfi ve sıra sayısı
olarak kullanmaktansa, bilhassa sabit uzuv boyutlarını yerleştirdiğimiz
hücrelere isimler verelim. Bu isimler aşağıda verilen excel tablosunda
gösterilmektedir. Sabit uzuv değerleri bu gösterilen hücrelere girildikten
sonra, ![]() 1
ve
1
ve ![]() 2
açıları ile A0B0
ve B0C0
uzunlukları bulunmalıdır. Bunun için Visual Basic te yazmış olduğumuz
Açı ve Boy fonksiyonlarını kullanalım. Örneğin hücre ismi
Alfa1 olan B5 hücresinde =Açı(SabitU_Y,SabitU_D) ve hücre
ismi SabitUzuv olan B6 hücresine ise =Boy(SabitU_Y,SabitU_D)
komutunu girmemiz yeterli olacaktır (INSERT menüsü altında functions seçeneğini
seçerseniz kullanıcı tarafından tanımlanmış fonksiyonlar anlamına gelen
"user defined functions" olarak tanımlamış olduğunuz fonksiyonları
görebilirsiniz). Ek 2de verilmiş olan basit mekanizmalarda açılar sabit
uzuv x-ekseni üzerinde olacak şekilde ölçüldüğünden örneğin kol-kızak
mekanizması için giriş kolu açısından
2
açıları ile A0B0
ve B0C0
uzunlukları bulunmalıdır. Bunun için Visual Basic te yazmış olduğumuz
Açı ve Boy fonksiyonlarını kullanalım. Örneğin hücre ismi
Alfa1 olan B5 hücresinde =Açı(SabitU_Y,SabitU_D) ve hücre
ismi SabitUzuv olan B6 hücresine ise =Boy(SabitU_Y,SabitU_D)
komutunu girmemiz yeterli olacaktır (INSERT menüsü altında functions seçeneğini
seçerseniz kullanıcı tarafından tanımlanmış fonksiyonlar anlamına gelen
"user defined functions" olarak tanımlamış olduğunuz fonksiyonları
görebilirsiniz). Ek 2de verilmiş olan basit mekanizmalarda açılar sabit
uzuv x-ekseni üzerinde olacak şekilde ölçüldüğünden örneğin kol-kızak
mekanizması için giriş kolu açısından ![]() 1değerini
çıkarmamız ve ve çıkış kolu açısına ise aynı
1değerini
çıkarmamız ve ve çıkış kolu açısına ise aynı ![]() 1değerini
eklememiz gereklidir. Ayrıca
1değerini
eklememiz gereklidir. Ayrıca ![]() 13
açısını elde etmek için çıkış kolu açısından 900
çıkarmamız gereklidir.
13
açısını elde etmek için çıkış kolu açısından 900
çıkarmamız gereklidir. ![]() 13
değerini giriş kolu açısından elde etmek için KolKızak(A,B,theta)
fonksiyonunu kullanmamız yeterli olacaktır. Bu fonksiyonu kullanmak için
ilk olarak A13-A31 hücrelerine 20 şer derece aralıkta giriş kolu açısı
değerlerini yerleştirelim. B13 hücresinde A13 de verilmiş olan açı değerini
radyana çevirelim (=A13*pi()/180 yazarak veya =RADIANS(A13) komutu ile).
C13 hücresinde ise =KolKızak(Krank;SabitUzuv;(B13-Alfa1))+Alfa1-PI()/2
yazdığımızda
13
değerini giriş kolu açısından elde etmek için KolKızak(A,B,theta)
fonksiyonunu kullanmamız yeterli olacaktır. Bu fonksiyonu kullanmak için
ilk olarak A13-A31 hücrelerine 20 şer derece aralıkta giriş kolu açısı
değerlerini yerleştirelim. B13 hücresinde A13 de verilmiş olan açı değerini
radyana çevirelim (=A13*pi()/180 yazarak veya =RADIANS(A13) komutu ile).
C13 hücresinde ise =KolKızak(Krank;SabitUzuv;(B13-Alfa1))+Alfa1-PI()/2
yazdığımızda ![]() 13
açısını radyan cinsinden elde edebiliriz. D13 de bu açıyı dereceye çevirebiliriz.
E13 hücresinde ise
13
açısını radyan cinsinden elde edebiliriz. D13 de bu açıyı dereceye çevirebiliriz.
E13 hücresinde ise ![]() 15
açısını hesap edebilmek için Visual Basic ile hazırlamış olduğumuz DörtÇubuk()
fonksiyonundan yararlanmamız mümkündür. Bunun için E13 hücresine =
DörtÇubuk(Krank2; Biyel; ÇıkışUzvu; SabitUzuv4;1; (C13+ Alfa2p ) ) - Alfa2p
yazmamız yeterli olacaktır. F13 hücresinde ise bu açıyı dereceye çevirebiliriz.
Bu işlemlerden sonra ise B13-F13 hücrelerini seçer, F13 hücresinin sağ
alt köşesinde imlecimiz "+" olduktan sonra farede sol tuşu bastırır F31ye
kadar çeker bırakır isek, her 200 de
çıkış kolu açısını belirlemiş oluruz (tabiiki işlemleri her derecede bir
yapmak aynı şekilde mümkündür). Burada sonuçları bir sayfa içinde gösterebilmek
için aralık büyük alınmıştır). Sonuç değerleri Excel grafik komutu ile
kolayca çizebiliriz.
15
açısını hesap edebilmek için Visual Basic ile hazırlamış olduğumuz DörtÇubuk()
fonksiyonundan yararlanmamız mümkündür. Bunun için E13 hücresine =
DörtÇubuk(Krank2; Biyel; ÇıkışUzvu; SabitUzuv4;1; (C13+ Alfa2p ) ) - Alfa2p
yazmamız yeterli olacaktır. F13 hücresinde ise bu açıyı dereceye çevirebiliriz.
Bu işlemlerden sonra ise B13-F13 hücrelerini seçer, F13 hücresinin sağ
alt köşesinde imlecimiz "+" olduktan sonra farede sol tuşu bastırır F31ye
kadar çeker bırakır isek, her 200 de
çıkış kolu açısını belirlemiş oluruz (tabiiki işlemleri her derecede bir
yapmak aynı şekilde mümkündür). Burada sonuçları bir sayfa içinde gösterebilmek
için aralık büyük alınmıştır). Sonuç değerleri Excel grafik komutu ile
kolayca çizebiliriz.
| A | B | C | D | E | F | G | |
| 1 | |||||||
| 2 | Krank | Krank2 | |||||
| 3 | SabitU_Y | Biyel | |||||
| 4 | SabitU_D | ÇıkışUzvu | |||||
| 5 | Alfa1 | SabitU_Y4ç | |||||
| 6 | SabitUzuv | SabitU_D4ç | |||||
| 7 | Alfa2 | ||||||
| 8 | Alfa2p | ||||||
| 9 | SabitUzuv4 |
İsim verilen hücreler
| A | B | C | D | E | F | G | |
| 1 | KOL-KIZAK | DÖRT-ÇUBUK | |||||
| 2 | a2 | 510 | b2 | 1160.00 | |||
| 3 | a1 | 1250 | b3 | 1995.00 | |||
| 4 | b1 | 200 | b4 | 820.00 | |||
| 5 | a1 | 0.1586553 | 9.0902769 | c1 | 1700.00 | ||
| 6 | A0B0 | 1265.8989 | d1 | 600.00 | |||
| 7 | |
2.80 | 160.55997 | ||||
| 8 | |
0.34 | 19.440035 | ||||
| 9 | B0C0 | 1802.78 | |||||
| 10 | |||||||
| 11 | |||||||
| 12 | |
||||||
| 13 | 0 | -0.1586553 | 1.9303575 | 110.60 | 2.0131936 | 115.35 | |
| 14 | 20 | 0.1904106 | 1.7080406 | 97.86 | 1.6884444 | 96.74 | |
| 15 | 40 | 0.5394764 | 1.4946539 | 85.64 | 1.3955571 | 79.96 | |
| 16 | 60 | 0.8885423 | 1.3629073 | 78.09 | 1.2159721 | 69.67 | |
| 17 | 80 | 1.2376081 | 1.3161515 | 75.41 | 1.1518678 | 66.00 | |
| 18 | 100 | 1.586674 | 1.3292533 | 76.16 | 1.1698627 | 67.03 | |
| 19 | 120 | 1.9357398 | 1.3801176 | 79.07 | 1.2394982 | 71.02 | |
| 20 | 140 | 2.2848057 | 1.454262 | 83.32 | 1.3405772 | 76.81 | |
| 21 | 160 | 2.6338715 | 1.5425227 | 88.38 | 1.4607571 | 83.70 | |
| 22 | 180 | 2.9829374 | 1.6387942 | 93.90 | 1.592535 | 91.25 | |
| 23 | 200 | 3.3320032 | 1.7385706 | 99.61 | 1.7312095 | 99.19 | |
| 24 | 220 | 3.6810691 | 1.8380047 | 105.31 | 1.8736639 | 107.35 | |
| 25 | 240 | 4.0301349 | 1.9331863 | 110.76 | 2.0176373 | 115.60 | |
| 26 | 260 | 4.3792008 | 2.0193991 | 115.70 | 2.1611884 | 123.83 | |
| 27 | 280 | 4.7282666 | 2.0901106 | 119.75 | 2.301759 | 131.88 | |
| 28 | 300 | 5.0773325 | 2.135382 | 122.35 | 2.4296394 | 139.21 | |
| 29 | 320 | 5.4263983 | 2.1394725 | 122.58 | 2.446482 | 140.17 | |
| 30 | 340 | 5.7754642 | 2.0789423 | 119.11 | 2.2769452 | 130.46 | |
| 31 | 360 | 6.12453 | 1.9303575 | 110.60 | 2.0131936 | 115.35 |
Excel tablosu
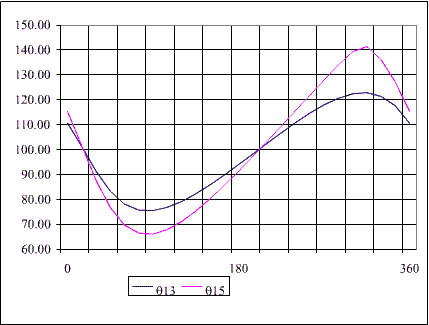
Grafik çıktı
Yukarıda gösterilen işlemlerin Excel kütüğü için (fivelink.xls) tıklayınız.
Örnek
Bu örnekte MathCad® paket programı kullanılacaktır. Bu
çeşit programlar her türlü matematik denklemi (sayısal veya sembolik olarak)
çözmek için geliştirilmişlerdir. Excel gibi programlarda genel olarak
sonucun yer aldığı veya kendi yerleştirdiğimiz değerlerin olduğu hücrelerin
her biri ayrı ayrı görülmekte, bir hücreye koyduğumuz değerleri oluştururken
yaptığımız işlemler perde arkasında kalmaktadır. Mathcad türü programlarda
ise bu hücreleri kolon harfi ve satır sayısı ile adlandırmaktansa biz
hücre kapağına bir etiket yerleştirip üstüne bu hücreyi temsil edecek
istediğimiz herhangi bir isim koyabiliriz. Bu durumda o hücrenin içinde
ne olduğunu etiketteki bu isimden biliriz. Ancak hücrenin kapağını açmadan
içinde ne kadar olduğunu bilemeyiz. Yani Excelde kapaksız olan hücrelerin
her birine kapak ve kapakların üzerinede birer etiket konmuştur (Excelde
bir hücreye ad verseniz bile etiketin üzerinde bulunan adı ancak imleci
hücreye götürdüğünüz zaman görebilirsiniz). MathCadde örneğin eğer : a:=120
, b:=50, ![]() :=20,
vb. tuşlarsanız program bilgisayar hafızasının bir yerinde oluşturduğu
hücrelere a,b,c ve q etiketleri yerleştirecek ve sizin belirtmiş olduğunuz
bu değerleri (sırası ile 120, 50 ve 20) bu hücrelere yerleştirecektir.
(bu işlem sırasında siz etiket ismini yazdıktan sonra ":" (iki nokta üst
üste) sembolünü girdiğinizde ekranda ":=" görülür ve bilgisayar etiketini
yerleştirdiğiniz hücreye değer girmenizi bekler. Bilgisayar etiketi yapıştırılmış
ancak içi boş bir hücreyi boşu boşuna tutmaz). Ayrıca paket program ile
bazı özel sayılar bazı hücrelere önceden yerleştirilmiştir ve bu isimleri
kullanamazsınız. Örneğin önceden etiketinde
:=20,
vb. tuşlarsanız program bilgisayar hafızasının bir yerinde oluşturduğu
hücrelere a,b,c ve q etiketleri yerleştirecek ve sizin belirtmiş olduğunuz
bu değerleri (sırası ile 120, 50 ve 20) bu hücrelere yerleştirecektir.
(bu işlem sırasında siz etiket ismini yazdıktan sonra ":" (iki nokta üst
üste) sembolünü girdiğinizde ekranda ":=" görülür ve bilgisayar etiketini
yerleştirdiğiniz hücreye değer girmenizi bekler. Bilgisayar etiketi yapıştırılmış
ancak içi boş bir hücreyi boşu boşuna tutmaz). Ayrıca paket program ile
bazı özel sayılar bazı hücrelere önceden yerleştirilmiştir ve bu isimleri
kullanamazsınız. Örneğin önceden etiketinde ![]() yazılı bir hücrede 3.141592654 sayısı bulunmaktadır. Excel de olduğu gibi,
çeşitli matematik işlem fonksiyonları programda mevcuttur.
yazılı bir hücrede 3.141592654 sayısı bulunmaktadır. Excel de olduğu gibi,
çeşitli matematik işlem fonksiyonları programda mevcuttur.
Örneğin xa:a*cos( ![]() *
*![]() /180)+b
işlemini tuşladığınızda ekranda:
/180)+b
işlemini tuşladığınızda ekranda:

Denklemini görürsünüz. Bu işlemle, etiketinde xa yazılı yeni bir hücre
oluşturulmuş ve denklemin sağında yazılmış olan operasyonlar ile a,b ve
![]() hücrelerinde
bulunan değerler kullanılarak gösterilen matematiksel işlemlerle yeni
bir değer elde edilerek bu hücreye yerleştirilmiştir. MathCad de bulunan
fonksiyonları unutur iseniz INSERT menüsünden fonksiyonlara bakabilirsiniz
(veya Help Menüsünden "functions" diye arayabilirsiniz). Eğer hücrenin
içeriğini görmek isterseniz bu denklemin altında veya sağında bir yere
xa = tuşlamalısınız. Eğer a:=120, b:=50,
hücrelerinde
bulunan değerler kullanılarak gösterilen matematiksel işlemlerle yeni
bir değer elde edilerek bu hücreye yerleştirilmiştir. MathCad de bulunan
fonksiyonları unutur iseniz INSERT menüsünden fonksiyonlara bakabilirsiniz
(veya Help Menüsünden "functions" diye arayabilirsiniz). Eğer hücrenin
içeriğini görmek isterseniz bu denklemin altında veya sağında bir yere
xa = tuşlamalısınız. Eğer a:=120, b:=50,
![]() :=20
değerleri önceden yazılmış ise, ekranda xa=143.969
değerini göreceksiniz. Yani bu durumda kullan-dığınız denklemler ekranda
istediğiniz yerlerde (ancak belirli bir sırada) olabilir. Her hangi bir
hücre değerini bilmek istiyor iseniz hücre adını yazdıktan sonra eşit
işaretini koymak yeterlidir. Tüm formülleri bir kitapta yazıldığı gibi
görmek mümkündür. Şimdi bu kavramları bir mekanizmanın analizinde kullanalım.
:=20
değerleri önceden yazılmış ise, ekranda xa=143.969
değerini göreceksiniz. Yani bu durumda kullan-dığınız denklemler ekranda
istediğiniz yerlerde (ancak belirli bir sırada) olabilir. Her hangi bir
hücre değerini bilmek istiyor iseniz hücre adını yazdıktan sonra eşit
işaretini koymak yeterlidir. Tüm formülleri bir kitapta yazıldığı gibi
görmek mümkündür. Şimdi bu kavramları bir mekanizmanın analizinde kullanalım.
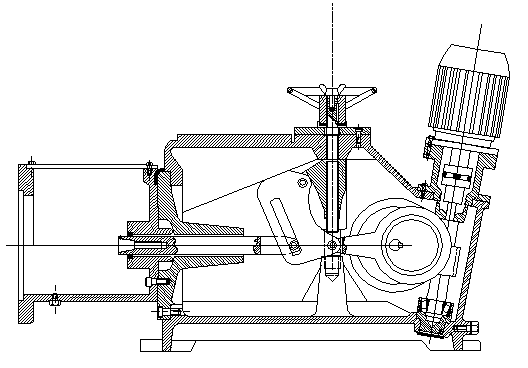
Yukarıda ayarlı bir pompa mekanizması görülmektedir. Eksantrik olarak tasarlanmış olan krank mili bir elektrik motorundan sonsuz vida - dişli sistemi ile devir sayısı gerektiği kadar düşürüldükten sonra döndürülmektedir.

Mekanizmanın şematik görünümü Şekil yukarıda gösterildiği gibidir. Pompanın kurs boyu ayarlaması B0 mafsal noktasının bir ayar vidası ile yukarı aşağı hareket ettirilerek, s1 uzunluğu değiştirilerek, yapılmaktadır.

A0ABB0 devresi (1,2,3 ve 4 uzuvları) bir dört çubuk mekanizmasını oluşturmaktadır. Önceki örneklerden farklı olarak A0B0 sabit mafsal noktaları yatay değildirler, B0 noktası A0 noktasının solunda ve yukarısındadır. Yine de vektör devre denklemi (A0A + AB = A0B0 + B0B) aynı şekilde yazılabilir:
Vektör denklemi
B0A
= B0A0
+ A0A
s![]() =
b1 - is1 +
a2
=
b1 - is1 +
a2![]()
eğer reel ve sanal kısımlar ayrı ayrı eşitlenir ise:
s cos![]() =
b1 + a2
cos(
=
b1 + a2
cos(![]() 12)
12)
s sin![]() =
s1 + a2
sin(
=
s1 + a2
sin(![]() 12)
12)
Önceden gösterildiği gibi s ve ![]() değerleri
bu iki denklemden çözülebilir . Bundan sonra B0AB
üçgeni kullanılarak (üç kenarı biliniyor)
değerleri
bu iki denklemden çözülebilir . Bundan sonra B0AB
üçgeni kullanılarak (üç kenarı biliniyor) ![]() açısı
kosünüs teoremi ile bulunur:
açısı
kosünüs teoremi ile bulunur:
![]()
![]() 14
açısı:
14
açısı:
![]() 14=
14=
![]() -
-![]() -
-![]() /2
/2

Pompanın ikinci kısmını oluşturan ve yukarıda gösterilen çift kızaklı mekanizma için (1,4 ve 5 uzuvları), vektör devre denklemi kompleks sayılarla:
c4
![]() + is4
+ is4
![]() = -is1
- s15 + b1
= -is1
- s15 + b1

MathCAD ile çözüm yapılırken bu denklemleri aynen yazmak yeterlidir.
Ancak her hangi bir işlem yapmadan önce sayısal parametrelerin (bağımsız
değişken veya sabit parametrelerin) değerleri mutlaka programda yazılmalıdır.
Program tanımlanmamış veya içi boş hücreler ile işlem yapamaz.![]() 12
= 3200 için Mathcad sayfası aşağıda
olduğu gibi görülecektir.
12
= 3200 için Mathcad sayfası aşağıda
olduğu gibi görülecektir.
MathCad Sayfası - 1
Ayarlanabilir Pompa
Verilen bir krank açısına göre çıkış uzvu konumu:
![]() (derece
ile verilen açı değerini radyana çevirme)
(derece
ile verilen açı değerini radyana çevirme)
A0A = a2:=55 AB = a3:=240 BB0 = a4:=165 b1:=185 s1:=90 c4:=70
![]() :=320
:=320
![]() :=
:=![]() .conv
(derece olarak verilen açı radyana çevrildi)
.conv
(derece olarak verilen açı radyana çevrildi)
xa
:= b1 + a2
.cos(![]() )
ya := -s1
+ a2 .sin(
)
ya := -s1
+ a2 .sin(![]() )
(uzuv boyutları ve bağımsız parametre değeri)
)
(uzuv boyutları ve bağımsız parametre değeri)
| |
(yatay ve dikey bileşenleri xa,ya olan vektörün yatay ile yaptığı açıyı belirlemek için "angle" fonksiyonu) |
 (Kosinüs teoremi)
(Kosinüs teoremi)

Eğer hareket analizini mekanizmanın tüm konumları için yapmak ister isek;
örneğin krank açısının her 50 aralığında
00 dan 3600
aralıkda değerlerin hesaplanması gerekli ise, bu durumda hücrelere yazacağımız
etiketlerde isim bulmakta zorluk çekebileceğimizden indis kullanmamız
gerekli olacaktır. Oluşacak 73 krank açısının her birini ![]() i
olarak (i=0,1,..72) gösterir isek, 73 hücre tanımlanmış olacaktır ve
i
olarak (i=0,1,..72) gösterir isek, 73 hücre tanımlanmış olacaktır ve ![]() 0
a 00 yerleştirilirken
0
a 00 yerleştirilirken ![]() 10
da 500 olacaktır. Bu durumda her etapta
tüm bu açılar için hesap yapıldığından alacağımız her cevapta 73 değerli
olacaktır. İkinci olarak elde ettiğimiz bu değerleri MathCad'in grafik
komutu kullanarak çizdirmemiz mümkün olacaktır (Excel de indis yerine
satırlar kullanılarak çok sayıda hücre elde edilmişti. Burada indisin
kullanılması gerekmektedir).
10
da 500 olacaktır. Bu durumda her etapta
tüm bu açılar için hesap yapıldığından alacağımız her cevapta 73 değerli
olacaktır. İkinci olarak elde ettiğimiz bu değerleri MathCad'in grafik
komutu kullanarak çizdirmemiz mümkün olacaktır (Excel de indis yerine
satırlar kullanılarak çok sayıda hücre elde edilmişti. Burada indisin
kullanılması gerekmektedir).
MathCad Sayfası - 2
Ayarlanabilir Pompa
Tüm devir analizi:



Yukarıda s15 in krank açısına göre
değişimi görülmektedir. Ancak s1 mesafesi
bir ayar vidası ile değiştirilmektedir. Eğer bu mesafenin 5 uzvu hareketine
etkisi incelenmek istenir ise, s15 konum
parametresinin s1 e göre nasıl değiştiği
belirlenmelidir. Bunun için değişkenlerde iki indis birlikte kullanılmalıdır
(bir indis değişik ![]() 12
açısı değerleri için diğer indis ise değişik s1
değerleri için. Sonuç MathCad yazılımı aşağıda görüldüğü gibi olur.
12
açısı değerleri için diğer indis ise değişik s1
değerleri için. Sonuç MathCad yazılımı aşağıda görüldüğü gibi olur.
MathCad Sayfası - 3
Ayarlanabilir Pompa
Tüm bir devir ve değişik ayar durumları için analiz


Görüldüğü gibi, s1 mesafesi azaldıkça, piston stroku azalacak, arttıkca strok artacaktır.
Örnek
Bir önceki MathCad ile çözülmüş olan denklemler Excel paket programı
kullanılarak aynen çözülebilir. Tabii ara basamaklar daha fazla olduğundan,
kullanılacak olan kolon sayısı fazla olur. Normal Excel Komutları yerine
bu işlemlerin tümünü yapan, verilen ![]() 12
krank açısına ve s1 ayar mesafesine
karşı gelen s15 mesafesini hesap eden
tek bir fonksiyonu kendimiz yazabiliriz. Bu şekilde tıpkı bir açının kosinüsünü
alır gibi, bu fonksiyon kullanılarak s15
mesafesi tek bir işlemde bulu-nabilir. Bunun için "Tools" menüsünden "Macro"
alt menüsünü seçelim ve buradan "Visual Basic Editor" olanağını açalım.
Bu editör kullanılarak hertürlü program yazılabilir. Biz bir fonksiyon
programı yazalım ve adı AyarlıPompa olsun. Bu program aşağıda gösterildiği
gibi olabilir (Programcıya göre tabiiki programın yazılımı bazı farklılıklar
gösterecektir)
12
krank açısına ve s1 ayar mesafesine
karşı gelen s15 mesafesini hesap eden
tek bir fonksiyonu kendimiz yazabiliriz. Bu şekilde tıpkı bir açının kosinüsünü
alır gibi, bu fonksiyon kullanılarak s15
mesafesi tek bir işlemde bulu-nabilir. Bunun için "Tools" menüsünden "Macro"
alt menüsünü seçelim ve buradan "Visual Basic Editor" olanağını açalım.
Bu editör kullanılarak hertürlü program yazılabilir. Biz bir fonksiyon
programı yazalım ve adı AyarlıPompa olsun. Bu program aşağıda gösterildiği
gibi olabilir (Programcıya göre tabiiki programın yazılımı bazı farklılıklar
gösterecektir)
Global Const PI = 3.1415926
Function AyarlıPompa(A_2,A_3, A_4, B_1, C_4, S_1, ThetaDerece)
Dim Xa, Ya As Double
Dim S, fi, si, Theta2, Theta4 As Double
Dim S_4 As Double
Theta2 = ThetaDerece * PI / 180
Xa = B_1 + A_2 * Cos(Theta2)
Ya = -S_1 + A_2 * Sin(Theta2)
S = Boy(Xa, Ya)
fi = Açı(Xa, Ya)
si = AçıCos(A_4, S, A_3)
Theta4 = fi - si - PI / 2
S_4 = -(S_1 + C_4 * Sin(Theta4)) /
Cos(Theta4)
AyarlıPompa = B_1 - C_4 * Cos(Theta4)
+ S_4 * Sin(Theta4)
End Function
AyarlıPompa() fonksiyonundaki denklemler, analiz sonucunda elde ettiğimiz denklemlerin BASIC lisanı ile yazılımıdır. Ayrıca bu fonksiyon içinde, Boy(X,Y) (X ve Y boyutları verildiğinde hipotenüs bulma), Açı(X,Y) (X ve Y değerleri verildiğinde açı bulma), AçıCos(U1,U2,U3) (Kosinüs teoremine göre üç kenarı verilen bir üçgenin U3 kenarının karşısındaki iç açıyı bulma) gibi üç ayrı fonksiyonu kullanmaktadır. Kullanılan bu fonksiyonlar EK-2 de verilmiştir.
Bu fonksiyon kullanılmadan önce sabit uzuv boyutlarını B1-B5 hücrelerine sırası ile yerleştirelim ve bu hücrelere sırası ile Krank, Biyel, Arakol, SabitU_Y, ve Eksantrik isimlerini verelim. B7 hücresine ise vidanın bir ayar boyutuna gelen s1 uzunluğunu yerleştirelim (s1=20mm).
İkinci olarak A8 - A26 hücrelerine krank açısını her 200 için yerleştirelim (ilk iki hücre doldurulduktan sonra, fare ile sağ alt köşeden tutup, A26 hücresine kadar uzatılabilir.
İmleci B8 hücresine getirelim. Basic lisanı ile yazmış olduğumuz fonksiyonu
kullanmak için bu hücreye = AyarlıPompa(Krank; Biyel; Arakol; SabitU_Y;
Eksantrik; B$7; $A8 ) komutunu tuşlayalım. Bu komut hazırlanmış olan
program devreye girer ve A8 hücresindeki ![]() 12
açısı, B7 hücresindeki s1 değeri ve
isimlendirmiş olduğumuz hücrelerde bulunan uzuv boyutlarına göre piston
konumu s15 bu programdaki işlem sırası
ve komutlarına göre bulunur. B8 hücresini B26 ya kadar kopyaladığımızda
tüm krank açıları için piston konumu bulunacaktır. Kopyalama sırasında
B7 hücresinin dikeyde değişmemesi için B$7 yazılmıştır (yatayda değişebilir).
Kopyalama sırasında krank açısı için $A8 yazıldığından 8 rakamı her satırda
o satır numarasını alacaktır ($A yazıldığından dolayı dikeyde değişmeyip
daima A kolonu olacaktır).
12
açısı, B7 hücresindeki s1 değeri ve
isimlendirmiş olduğumuz hücrelerde bulunan uzuv boyutlarına göre piston
konumu s15 bu programdaki işlem sırası
ve komutlarına göre bulunur. B8 hücresini B26 ya kadar kopyaladığımızda
tüm krank açıları için piston konumu bulunacaktır. Kopyalama sırasında
B7 hücresinin dikeyde değişmemesi için B$7 yazılmıştır (yatayda değişebilir).
Kopyalama sırasında krank açısı için $A8 yazıldığından 8 rakamı her satırda
o satır numarasını alacaktır ($A yazıldığından dolayı dikeyde değişmeyip
daima A kolonu olacaktır).
AyarlıPompa fonksiyonu artık Excel de hazır herhangi bir fonksiyon programı gibi kullanıma hazırdır.
s1 mesafesi bir ayar vidası ile değiştirilmektedir. Eğer bu ayarın 5 uzvunun hareketine etkisi incelenmek istenir ise, s15 konum parametresinin s1 e göre nasıl de-ğiştiği belirlemek gerekecektir. Bunun için B7, C7, D7, E7, F7 ve G7 hücrelerine değişik s1 değerleri yerleştirilmiştir. B8 hücresinde yazmış olduğumuz formülü şimdi B8-G27 arasında bulunan tüm hücrelere kopyalamamız gerekecektir. C kolonuna gelindiğinde s1 in bulunduğu hücreler B$7 şeklinde yazıldığından, B yerine C kolon harfi gelecek ancak hangi satırda olursak olalım, satır sayısının önüne $ işareti bulunduğundan (B$7) C kolonunun her hangi bir hücresine formül kopyalandığında, C7 hücresindeki s1 değeri kullanılacaktır. Benzer bir şekilde C kolonuna gelindiğinde krank açısı olarak $A8 yazıldığından krank açısı değeri mutlaka A kolonunda bulunan hücre olacak ve bulunduğumuz satır A kolonunda kullanılacak olan krank değerinin bulunduğu satır ile aynı olacaktır. Sonuç Şekil aşağıda de görülmektedir ve Mathcad ile yapılmış olan çözüm ile aynıdır. Excel kütüğü için (ayarlıpompa.xls) tıklayınız.
| A | B | C | D | E | F | G | |
| 1 | A2 | 55 | |||||
| 2 | A3 | 240 | |||||
| 3 | A4 | 165 | |||||
| 4 | B1 | 185 | |||||
| 5 | C4 | 70 | |||||
| 6 | |||||||
| 7 | 20 | 50 | 100 | 150 | 200 | 250 | |
| 8 | 0 | 252.0937 | 247.4078 | 249.6989 | 254.5738 | 251.8945 | 231.2036 |
| 9 | 20 | 252.1405 | 245.7816 | 248.1027 | 255.8408 | 258.3663 | 245.9161 |
| 10 | 40 | 252.2511 | 245.3691 | 249.6373 | 261.9564 | 270.8585 | 266.6617 |
| 11 | 60 | 252.2215 | 246.2394 | 254.6551 | 273.3395 | 289.4999 | 292.9677 |
| 12 | 80 | 252.0927 | 248.7137 | 263.8473 | 290.7546 | 314.6072 | 324.3855 |
| 13 | 100 | 252.2614 | 253.48 | 278.3194 | 315.0693 | 345.947 | 359.3292 |
| 14 | 120 | 253.5854 | 261.6704 | 299.246 | 346.0074 | 380.8984 | 393.3704 |
| 15 | 140 | 257.3465 | 274.4691 | 325.9924 | 379.1378 | 412.1455 | 418.5263 |
| 16 | 160 | 264.4316 | 291.0171 | 352.1259 | 403.739 | 429.014 | 426.5381 |
| 17 | 180 | 272.9428 | 305.118 | 365.8015 | 409.1448 | 425.2503 | 414.8999 |
| 18 | 200 | 277.6904 | 308.9373 | 361.3043 | 395.2032 | 404.2678 | 388.3058 |
| 19 | 220 | 276.148 | 302.3755 | 344.4052 | 370.4372 | 374.5207 | 354.1352 |
| 20 | 240 | 270.7803 | 291.0105 | 323.5058 | 343.1006 | 343.1258 | 318.3708 |
| 21 | 260 | 264.7198 | 279.2832 | 303.5609 | 317.7134 | 314.1433 | 284.8884 |
| 22 | 280 | 259.5959 | 269.1044 | 286.4366 | 296.0851 | 289.5916 | 256.4869 |
| 23 | 300 | 255.902 | 260.9577 | 272.5591 | 278.8124 | 270.5826 | 235.7459 |
| 24 | 320 | 253.6054 | 254.7785 | 261.8858 | 266.0913 | 257.8185 | 224.6681 |
| 25 | 340 | 252.4534 | 250.3422 | 254.2934 | 258.0019 | 251.617 | 223.5825 |
| 26 | 360 | 252.0937 | 247.4078 | 249.6989 | 254.5738 | 251.8945 | 231.2036 |
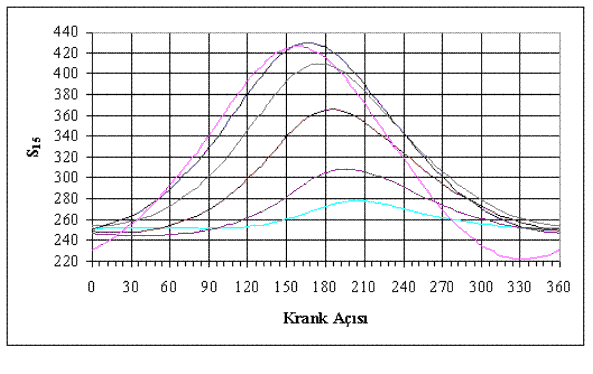
Hesaplama hassasiyeti ile ilgili not:
Bilgisayarlarda sayılar belirli sayıda rakam ile depo edilir. Örneğin Excel de sayılar 15 hane olarak depolanır. Hane sayısı programa ve bilgisayara göre 6 ila 64 arasında olabilir. Mekanizmaların analizi veya sentezi sırasında bu hassasiyet gereğinden fazladır ve çok hassas sonuçlar, eğer doğru yöntem kullanılır ise, alınabilir. Bu önlemlerden birincisi yapılacak hesaplama miktarının minimuma indirilmesi ve bilhassa bölme işlemlerinde paydanın sıfıra yakın olmamasına dikkat edilmesidir. Ayrıca mekanizmanın özel konumlarında (ölü konumlar, kilitlenme konumları gibi uzuvlarda mafsalların birkaçının aynı doğru üzerinde olması durumu) hassasiyet azalabilir ve ayrıca bilgisayardan hata (sıfıra bölme veya negatif bir sayının kökü gibi) mesajları alınabilir. Yapılan işlemler doğru ise, Bu aynı zamanda o mekanizmanın pratikte sorunu olacağını da gösterir.
Mühendislikte hiçbir sonuç başlangıç değerlerinden daha hassas olamaz. Bu nedenle elde edilen sonuç rakamlar sınırlı sayıda hane ile gösterilmelidir. Örneğin ±.1mm toleransla üretilmiş uzuvlardan oluşan bir mekanizmada sonuç s konum değişken değerini x=26.231456789mm olarak göstermek yanlıştır (mühendislik açısından mantıksızdır) x=26.2 ±.1mm den daha hassas elde edilmiş olamaz. Bu nedenle ekranda görülen rakamlar mutlaka kullanıcı tarafından incelenmelidir.

