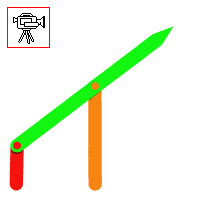
7.1 Dört Çubuk Mekanizması

Dört uzuvlu ve dört döner mafsala sahip mekanizmaya dört-çubuk mekanizması denmektedir. Genelde hareket eden üç uzuv görülse de, sabit gövde de bir uzuv sayılmaktadır.

Dört-çubuk mekanizmalarının uygulamada çeşitliliği hayret edici miktarlarda olup genelde kullanan kişiler onun bir mekanizma olduğunun bile farkına varmayabilirler. Uygulama alanı bu kadar geniş olsa bile, bu uygulamalar üç değişik gurupta toplanabilir:

a)

Sabit uzva bağlı uzuvların açısal dönme miktarları arasında belirli bir ilişkinin olması (bu fonksiyon sentezi olarak bilinir). Bu tür uygulamalarda giriş ve çıkış uzuvlarının açısal konumları arasında 14 = f(12) gibi bir fonksiyonun dört-çubuk mekanizması kullanılarak sağlanması istenmektedir. Buna basit bir örnek, aşağıda görüldüğü gibi, lineer bir ölçü ile dönmeyi (1< x <10) belirli bir aralıkda logaritmik bir ölçüde dönmeye (y = ln(x)) çevirmek olabilir. Bir pencerenin belirli bir açı kadar açılmasını uzak bir noktadan sağlama, bir vananın 900 açılmasını, bir kolun 1800 dönmesi ile sağlama (bu şekilde mekanik avantaj sağlanacaktır) gibi çok değişik alanlarda kullanılabilir (örneğin araç gaz pedalı)

 
b) Sabit uzva bağlı olmayan uzva biyel uzvu denmektedir. Bu uzuv üzerinde bulunan bir nokta (biyel noktası) sabit uzuv üzerinde bir eğri çizecektir. Genel olarak altıncı dereceden olan bu eğriye biyel eğrisi denir. Biyel eğrisi, uzuv boyutlarına ve biyel noktasının biyel üzerinde konumuna göre değişik şekillerde olabilir. Uygun uzuv boyutları ve biyel noktası seçimi ile biyel eğrisi belirli bir aralıkda bir doğruya, bir daireye veya başka bir eğriye (örneğin film sürme mekanizmasında bir kısmı bir doğru ile benzeşen D şeklinde bir eğri) benzeştirilebilir. Bu tür problemlere yörünge sentezi denmektedir.

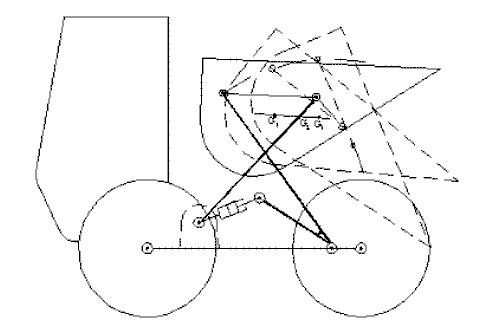
c) Biyel uzvunun değişik konumları bir dört-çubuk mekanizmasından istenilen bir hareket olabilir. Şekilde bir dört-çubuk mekanizması olan damperli kamyonda damper ağırlık merkezinin yükü boşaltması (damperin dönmesi) ve boşaltırken ağırlık merkezinin eğik bir doğru üzerinde olması istenmektedir. Benzer uygulama katlanabilir sandalye ve koltuklarda, yataklı kanapelerde görülebilir. Bu tür problemlere konum sentezi denmektedir.

 

 

 Grasshof Teoremi:

Bir mekanizmanın tipi uzuv boyutları ile değişmez isede hareket özellikleri tabiiki uzuv boyutlarına bağlıdır. Bir dört-çubuk mekanizmasında hareket özellikleri uzuv boyutlarının birbirlerine göre oranı ile belirlenecektir. Sabit uzva döner mafsal ile bağlı uzuvlar iki değişik hareket yapabilir:

i) Uzuv, sabit uzva göre tam bir dönme yapabilir. Bu tip uzva kol (krank) diyeceğiz.
ii) Uzuv belirli bir açısal aralıkda salınım yapabilir. Bu tip uzva sarkaç diyeceğiz.

Sabit uzva bağlı kolların krank veya sarkaç olmasına göre hareket açısından üç değişik dört-çubuk mekanizması oluşacaktır:

i) Sabit uzva bağlı iki uzuvda tam bir dönme yapabilir. Bu tipte dört-çubuk mekanizmasına "çift-krank " veya "çift-kol" diyeceğiz.
ii) Sabit uzva bağlı iki uzuvda sadece salınım yapabilir. Bu tipte dört-çubuk mekanizmasına "çift-sarkaç" diyeceğiz.
iii) k) Sabit uzva bağlı uzuvlardan birisi tam bir dönme yapabilir iken, diğer uzuv salınım yapabilir. Bu tipte dört-çubuk mekanizmasına "kol-sarkaç" diyeceğiz.

 

Dört-çubuk mekanizmasının hareket açısından değişik bu dört tipi uzuv boyutlarına bağlıdır. Grashof teoremi (veya Grashof kuralı) uzuv boyutlarına bağlı olarak bu değişik dört-çubuk mekanizmasını şu şekilde belirler:

Bir dört uzuvlu dört döner mafsallı zincirde:

      l = en uzun uzvun uzuv boyutu

      s = en kısa uzvun uzuv boyutu

      p,q = diğer uzuvların uzuv boyutları

Uzuv boyutları, önceden belirtildiği gibi, mafsal eksenleri arasında kalan mesafedir. Bu tanıma göre:

1. Eğer l + s < p + q ise (en uzun uzuv boyutu ile en kısa uzvun uzuv boyutu toplamı diğer iki uzvun uzuv boyutlarının toplamından kısa ise):

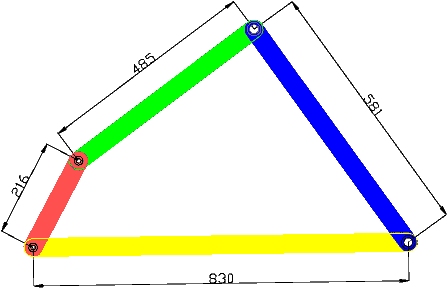
l=830, s=216 , p=485 , q=581

830+216=1046<485+581=1066

a,b) Eğer en kısa uzva komşu uzuvlardan birisi sabit ise, en kısa uzuv krank olmak üzere iki değişik kol sarkaç mekanizması elde edilir.(Yukarıda gösterilmekte olan mekanizmada en kısa uzuv =kırmızı uzuv olduğuna göre, komşu uzuvlar yeşil veya mavi uzuv sabit olduğunda kırmızı uzuv krank mavi uzuv ise sarkaçdır.)

 

c) Eğer en kısa uzuv sabit ise, dört-çubuk mekanizması çift kranktır.

d) Eğer en kısa uzvun karşısındaki uzuv sabit ise, dört-çubuk mekanizması çift sarkaçtır.

2. Eğer l + s > p + q (en uzun uzuv boyutu ile en kısa uzvun uzuv boyutu toplamı diğer iki uzvun uzuv boyutlarının toplamından fazla ise):

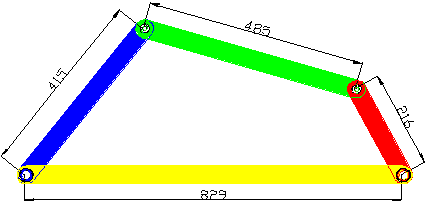
l=829, s=216 , p=485 , q=415

829+216=1045>485+415=900

Bu durumda hangi uzuv sabit olursa olsun sadece değişik salınım açıları olan çift sarkaç mekanizmaları elde edilecektir.
Elde edilen 8 değişik mekanizmanın animasyonları için tıklayınız.

3. Eğer l + s = p + q ise, (1) de açıklanmış olan üç değişik dört-çubuk mekanizması tipi elde edilir. Ancak bu mekanizmalarda tüm uzuvların bir doğru üzerinde olduğu bir kritik bir konum oluşacaktır.

Bu konumda her krank açısı için iki çıkış kolu açısı olan mekanizmada çözüm teke düşer. Bundan dolayı krankın bu konumdan hafif bir sapması durumunda hareketli diğer iki uzvun nasıl bir hareket yapacağı bilinemez. Örneğin, sabit uzva bağlı diğer kol saat yelkovanı yönünde veya ters yönünde dönebilir . Bu nedenle hareket belirsizdir.

4. i) (3) ün özel bir durumu çok bilinen paralelogram mekanizmasıdır Bu durumda karşı uzuv boyutları birbirlerine eşittir. Elde edilebilecek iki değişik çift kol mekanizması vardır. Ancak her iki çift kol mekanizmasınında kritik konumu olacak ve bu kritik konumda mekanizma çapraz bir konuma geçebilecektir.

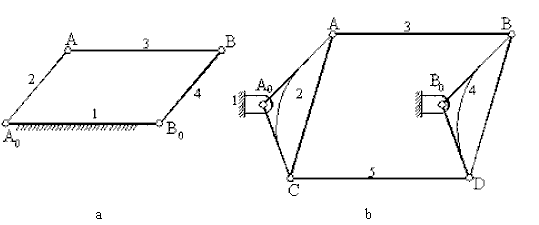
Mekanizmanın kritik konumlarında sorun olmaması için iki krank arasında iki değişik paralelogram mekanizması oluşturulabilir. Dikkat edilir ise, parallelogram mekanizmalarından birisi kritik konumda iken (örneğin A0ABB0 bir doğru üzerine olursa) diğeri kritik konumda olmayacağından mekanizma her konumda çift kol olarak hareket iletecektir.

ii) (3) ün bir diğer özel durumu ise deltoid mekanizmasıdır. Bu durumda iki aynı uzunlukta uzuv, iki aynı uzunlukta diğer uzuvlarla bağlıdır. Uzun uzuvlardan birisinin sabit olması ile bir kol-sarkaç meka-nizması elde edilebilir. Kısa uzuvlardan birinin sabit olması durumunda ise, kranklardan birisinin iki turu sırasında diğer krankın bir tur attığı bir çift-kol mekanizması elde edilebilir (bu mekanizmaya 1844 de patentini alan kişi olduğundan, Galloway mekanizmasıda denmektedir)

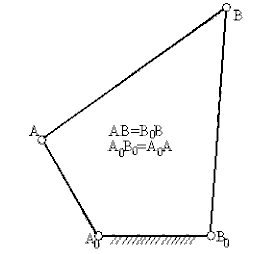
Dikkat edilir ise, uzuv boyutlarının tümünü bir sabit değer ile çarptığımızda veya böldüğümüzde uzuv boyutları arasında bulunan oran sabit kaldığı müddetce, mekanizmanın hareket özellikleri değişmeyeceği gibi, uzuvların birbirlerine göre açısal konumlarıda aynı kalacaktır. Yani, açısal değerler uzuv boyutlarının birbirlerine göre oranlarına bağlı olup, uzuv boyutlarına bağlı değildir. Bir başka deyişle, uzuv boyutlarının oranları sabit kalmak şartı ile bir dört-çubuk mekanizmasını ne kadar küçültürseniz küçültün, veya ne kadar büyütürseniz büyütün, giriş kolu açısına karşı gelen diğer kol açıları, uzuv boyu oranları aynı kaldıkca, daima aynıdır (mekanizmada oranların sabit kalarak mekanizmayı büyütme veya küçültme, mekanizmanın farklı ölçeklerde çizilmesi, veya devre denkleminin bir sabit değerle çarpılması olarakda düşünülebilir).

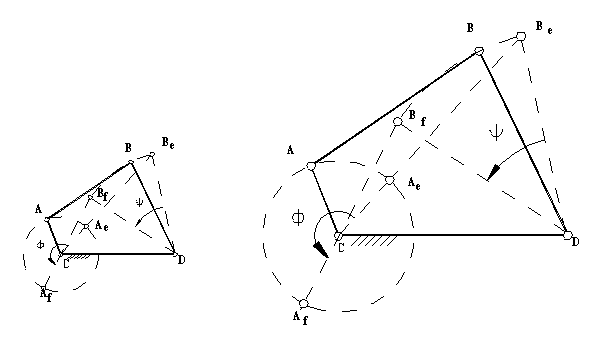
Mekanizmayı ne kadar büyütürseniz büyütün veya ne kadar küçültürseniz küçültün, eğer uzuv oranları aynı ise, açısal konumlar aynıdır.

Dört-çubuk mekanizmaları arasında kol-sarkaç mekanizması makina tasarımında önemli bir yer alır. Bu mekanizma kullanılarak bir elektrik motorunun sürekli bir dönüş hareketini kolayca bir salınım hareketine dönüştürülebilir. Bu nedenle kol-sarkaç oranlarına sahip dört-çubuk mekanizmalarının biraz daha detaylı incelenmesinde yarar bulunmaktadır.

Kol-sarkaç mekanizmalarının ölü konumları

Kol-sarkaç mekanizmasında sarkaç iki sınır açı değeri arasında salınır. Genellikle krank giriş uzvu olup sarkaç ise çıkış uzvudur. Sarkacın bir yöne doğru yapmakta olduğu salınım yavaşlar ve bir konumda durduktan sonra yön değiştirerek ters yöne doğru salınım yapar. Bu, krankın 3600 dönmesi sırasında iki defa tekrarlar. Sarkacın limit konumları, veya hızının sıfır olduğu konumlar, kol-sarkaç mekanizmasının ölü konumları olarak tanımlanır. Kısım 2 de dört-çubuk mekanizmasının hız analizinde her hangi bir konumda, 4 uzvunun açısal hızı için verilmiş olan denklem:

      (denklemin cıkarılışı için örnek-2)

Bu denklemde:

      sin(12-13)=0   ise giriş kolu hızı ne olursa olsun sarkaç hızı sıfır olacaktır.

      sin(12-13)=0 olması 12-13=0 (12=13) veya (13=12±p) olduğunda gerçekleşir.

Bu durumlarda biyel ve krank aynı doğru üzerindedir. Bu konumlara açık ve kapalı ölü konumlar denir.

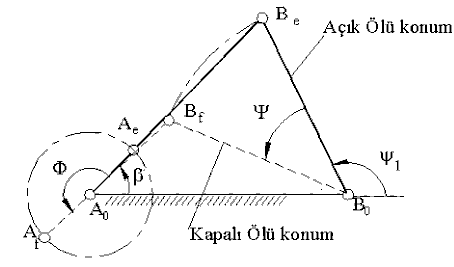
Salınım açısı, , sarkacın açık ölü konumdan kapalı ölü konuma geçerken yapmış olduğu açıdır.

Açık ölü konumdan kapalı ölü konuma hareket edilirken krankın yapmış olduğu dönme miktarı ise kadar, kapalı ölü konumdan açık ölü konuma hareket sırasında ise 3600- kadardır.

Genellikle sarkacın bir yönde hareketi sırasında iş yapılır diğer yönde sistem başlangıç noktasına boş olarak getirilir. Mühendis olarak genel hedefimiz sürati, dolayısı ilede verimliliği artırmakdır. Hız ise yapılan işin tipine bağlı olup maksimum çalışma hızı işin türü ile belirlenir. Ancak iş, sarkacın bir yönde dön-mesi sırasında yapılıyor ise, ters yönde dönme sırasında iş yapılmadığından sürat artırılabilir. Bu şekilde bir birim iş için geçen süre kısaltılabilir. Sabit dönen bir krank için bu, iş yapılan sarkaç dönme yönünde buna karşı gelen krank dönme açısını 1800 fazla olması, ters yönde hareket sırasında ise, krank dönme açısının 1800 az tutulması ile sağlanır. Bu durumda sabit krank dönme açısı için Zaman Oranı olarak:

      

tanımlanabilir. İş yapılırken krank dönme açısının fazla olması, geri dönüşte kalan krank dönme açısının azaltılması ile verim belirli bir miktar artırılacaktır.

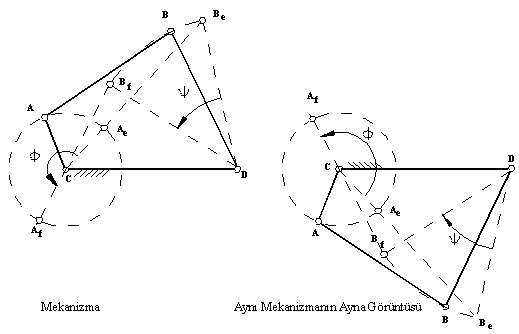
Kol-sarkaç oranlarında bir dört-çubuk mekanizmasını ele aldığımızda, bu mekanizmanın sabit uzva göre ayna görüntüsü alındığında yine bir kol-sarkaç oranında dört-çubuk mekanizması elde edilecek ve bu mekanizmanın salınım açısı orijinal mekanizma ile aynı olacaktır. Ancak krankın açık ölü konumdan kapalı ölü konuma orijinal mekanizmada açısı kadar saat yelkovanına ters yönde dönmesi gerekirken bu ayna görüntü mekanizmada 3600- kadar saat yelkovanına ters yönde dönmesi gerekecektir.

Bu sınır konumlara ölü konum denmesinin sebebi, bu konumlarda sarkaca etki eden kuvvet, mekanizmanın hareket etmesini sağlayamaz. Veya 14 açısal hızı ile sarkaç dönüyor ise, 2 uzvunun açısal hızı sonsuz olacaktır- ki bu mümkün değildir. Yani mekanizma, 4 uzvundan gelen herhangi bir uyarıya karşı ölüdür.

Bağlama Açısı

Kinematik analiz sırasında, bir mekanizmanın yük altında nasıl bir davranış göstereceğini bilmek önemlidir. Yük altında davranış olarak giriş uzvunda oluşan hareket ve kuvvet çıkış uzvuna nasıl ve ne şekilde iletildiğidir. Bu etapta hedefimiz kinematik analizini yaptığımız bir mekanizmanın yük altında davranışını belirlemek için kullanabileceğimiz bir kinematik parametre bulmaktır. Sürtünme ve atalet kuvvetleri ihmal edildiğinde, enerji sakınımından dolayı giriş uzvunda birim zamanda yapılan iş (T1212) çıkış uzvunda birim zamanda yapılan işe (T1414) eşittir. Bu değerler iki mekanizmada aynı olduğunda bile, kuvvet dağılımı açısından (mafsal kuvvetleri değerleri bakımından) iki mekanizma farklı özellikler gösterebilir. Şu ana kadar yapılmış olan kinematik analiz sırasında, moment ve kuvvet kavramları konu dışında olmuştur ve kullanacağımız kinematik parametre atalet kuvvetlerini hesaba almayacağından sadece mekanizmanın statik kuvvet özellikleri için bir fikir verebilecektir. Dinamik kuvvetlerin statik kuvvetlere göre çok büyük olduğu durumlarda bu parametrenin önemi kuşkulu olabilir. Ancak bütün bu olumsuzluklara rağmen, mekanizmanın yük altında davranışını gösterebilen bir kinematik parametre uygulamada önemlidir. Bu konu 1930 lu yıllarda Alt tarafından ortaya atılmış ve uygulamada önemi kanıtlanmıştır. Alt bağlama açısı () olarak:

      

tanımlamıştır. Bağlama açısı aynı zamanda:

      

Bağlama açısı mekanizmanın hareketi sırasında değişecektir. Sabit bir direnç karşısında gerekli sabit bir Ft kuvvetine karşı çıkış uzvuna hareketli mafsal noktasında etki eden toplam kuvvet de tüm hareket sırasında artar. Mekanizmanın mukavemet açısından tasarımı etki edecek olan maksimum kuvvete göre olacağından F kuvvetinin mümkün olduğunca Ft den büyük olmamasına çalışılmalıdır. Bu bağlama açısının hareket sırasında 900 den en az sapmasını gerektirir.

Şekilde yukarıda verilmiş olan tanıma göre bir dört-çubuk ve krank-biyel mekanizmasında bağlama açısı gösterilmektedir. Görüldüğü gibi, bağlama açısı basit bir kinematik parametre olup çıkış uzvuna giriş uzvundan iletilen kuvvetin ne kadarının iş yapar olduğunu göstermektedir. Bu basit parametre ile mekanizmanın uygulamada doğru çalışıp çalışmayacağını kinematik tasarım sırasında karar verilebilir. Aynı zamanda, bağlama açısının mekanizmada hareketin uzuv boyutlarındaki toleranslara karşı hassasiyetinide gösteren bir parametre olduğu bilinmektedir.

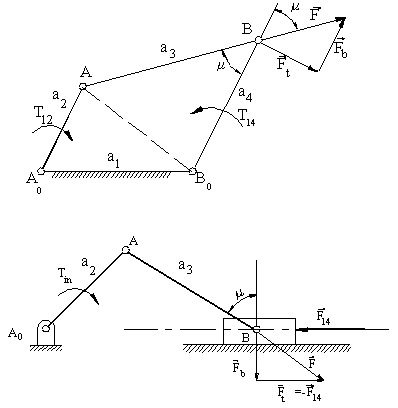
Bağlama açısı 900 olduğunda biyel uzvundan çıkış koluna iletilen tüm kuvvet çıkış kolunu çevirmek içindir. Bağlama açısının 00 olduğu durumda ise, giriş koluna ne kadar kuvvet uygularsak uygulayalım, çıkış kolunu çevrilemiyeceği açıkca görülmektedir. Ayrıca, bağlama açısının mekanizmanın sabit bir parametresi olmadığı, giriş kol açısına göre değişeceği açıktır. En optimum bağlama açısı 900, bir dört-çubuk mekanizmasının sadece bir veya iki giriş kolu açısında olacak, diğer konumlarda farklı bağlama açısı değerleri olacaktır. Öyle ise, dört-çubuk mekanizması için bağlama açısını giriş kolu açısına göre bulalım.

Bağlama açısını giriş kolu açısına göre belirlemek için ikinci kısımda konum analizi için kullandığımız yöntemi kullanmak uygun olacaktır. Şekilde gösterilen dört-çubuk mekanizması için A0AB0 üçgeni ile ABB0 üçgenlerini göz önüne alalım ve her iki üçgende kosinüs teoremini kullanarak AB0 uzunluğunu yazalım.

(1)

bu denklemden bağlama açısı çözüldüğünde:

(2)

veya:

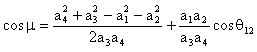(3)

olarak yazılabilir. Bağlama açısının minimum veya maksimum değerini elde etmek için (3) denkleminin 12 bağımsız değişkenine göre türevini alır ve d/d12 sıfıra eşitlenir ise:

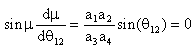(4)

Bu denklemden görüldüğü gibi bağlama açısı, 12=0 veya iken minimum veya maksimum değerde olacaktır ve bu konumlarda bağlama açısı değeri:

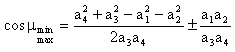(5)

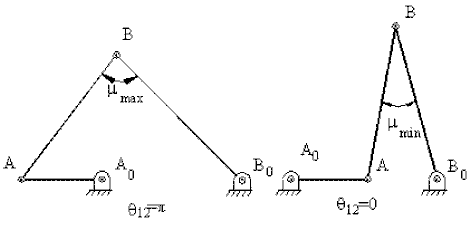
dir. Bu konumlar şekilde görülmektedir. En kritik bağlama açısı 900 dereceden en fazla sapan bağlama açısıdır. Bu nedenle min veya max değerlerinden her hangi birisi verilen uzuv boyutlarına göre daha kritik olabilir. Bazı yayınlarda 900 daha büyük bağlama açısı kullanılmayıp 900 den büyük açısında yerine (1800-) kullanıldığı ve bu şekilde iki farklı min değeri olduğu, bu değerlerden hangisi küçük ise, onun minimum bağlama açısı olduğuda gösterilmiştir. Bağlama açısı için bulunan 900 den en fazla sapma yapan değer, uygulamada kullanım yerine bağlı olarak değişir isede, 400 veya 500 den fazla olmaması önerilmektedir (900- min <400 veya 500 ) . Bu genel bir hatırlatma olup, bazı uygulamalar için 700 sapma müsaade edilebildiği gibi (örneğin uçak iniş takımları) bazı durumlarda ise 200 den az bir sapma olmamasına çalışılabilir (örneğin pompalar). Ancak uygulama tam olarak incelenememiş ise, maksimum sapmanın 400 ile 500 altında olmasına özen gösterilmesi gerekir.

(5) numaralı denklem incelendiğinde, uzuv boyutları:

a12+a22=a32+a42 (6)

denklemini sağladığı durumda, minimum ve maksimum bağlama açılarının 900 den sapması eşittir. Bu durum genel olarak optimum bir çözümdür. Bu özelliğe sahip dört-çubuk mekanizmalarına santrik dört-çubuk mekanizması denir ve zaman oranları 1 dir. Yani, sarkacın her iki yönde salınımı krankın 1800 dönmesi sırasında olur.

      1=|90-min|      2=|90-max|

      max=max(1,2)

 

Örnek

Bir dört-çubuk mekanizmasında uzuv boyutları: a2=4, a3=8, a4=6, a1=7 dir. Grashof kuralına göre 1 uzvu sabit uzuv 2 uzvu krank olmak üzere bu mekanizmanın bir kol-sarkaç olduğunu gösterin, salınım açısını, karşı gelen kol dönme açısını ve en kritik bağlama açısını bulun.

En uzun uzuv boyutu ile en kısa uzuv boyutu toplamı (4+8=12) diğer iki uzuv boyutu toplamından (6+7=13) az olması nedeni ile 2 uzvu krank, ona komşu 1 uzvu sabit ise mekanizma kol sarkaç oranını sağlamaktadır. Ölü konumlarda mekanizma üçgen şeklinde olduğundan bu konumlarda kosinüs teoremi uygulandığında:

Açık ölü konumda:

      

veya =20.850 ve

      

veya 1=45.380

Kapalı ölü konum için ise:

      

veya

      =217.960

      

veya

      =99.850

Bağlama açısının maksimum ve minimum değerleri ise:

      

      min=18.570 (1=71.430) ve max=102.640 (2=12.640).

min açısı 900 dereceden daha fazla sapma gösterdiğinden dolayı , min kritik bağlama açısıdır ve maksimum sapma 71.430 dir.

Alt Bağlama Açısı Problemi

Bağlama Açısı En İyi Olan Çift Kol Mekanizması Tasarımı

©es