7.2 Krank-Biyel Mekanizması
Makina tasarımında yoğun bir şekilde kullanılan bir başka mekanizmada krank-biyel mekanizmasıdır. Genel olarak bir dönme hareketini bir öteleme hareketine çevirmek için kullanıldığı gibi bir öteleme hareketini dönme hareketine çevirmek içinde kullanılabilir. Şekilde krank-biyel mekanizması, değişken açıları ve boyutları tanımlayan sabit parametreleri görülmektedir. Dört-çubuk mekanizmasında olduğu gibi, ölü konumlar krank ile biyelin aynı doğru üzerinde olduğu konumlardır. Krankın tam bir dönmesi için c eksantrikliğinin biyel ile krank uzunluklarının farkından az ve krankın en kısa uzuv boyutu olması gerekir. (yani c<(a3-a2) ve a3>a2 olmalıdır).
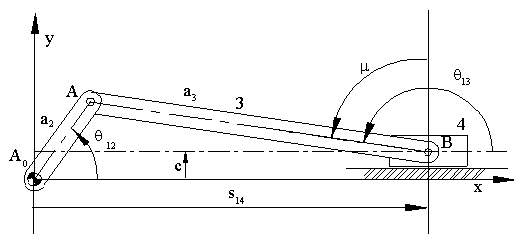
Krank biyel mekanizmasında strok (s) pistonun ölü konumlar arasında yaptığı öteleme mesafesi olup:
![]()
dur burada:
s = Strok
![]() =
a2/a3
=
a2/a3
![]() = c/a3
= c/a3
Eksantriklik sıfır ise( c = 0), krank biyel mekanizması santriktir ve bu durumda strok iki krank boyu olur (s = 2a2).
Bağlama açısı, ![]() ,
dört çubuk mekanizmasında verilmiş olan tanım ile aynı olup Şekilde görüldüğü
gibidir. Bağlama açısının dik açıdan sapması krank-biyel mekanizmalarında
daha önemli olup sürtünmeden dolayı kilitlenme (veya kasılma) ihtimali
daha fazladır. Ayrıca bağlama açısının dik açıdan sapması kayar mafsala
etki eden normal kuvveti artıracağından sürtünme kuvveti artacağından,
önemli enerji kaybına neden olur. Herhangi bir krank açısına göre bağlama
açısı:
,
dört çubuk mekanizmasında verilmiş olan tanım ile aynı olup Şekilde görüldüğü
gibidir. Bağlama açısının dik açıdan sapması krank-biyel mekanizmalarında
daha önemli olup sürtünmeden dolayı kilitlenme (veya kasılma) ihtimali
daha fazladır. Ayrıca bağlama açısının dik açıdan sapması kayar mafsala
etki eden normal kuvveti artıracağından sürtünme kuvveti artacağından,
önemli enerji kaybına neden olur. Herhangi bir krank açısına göre bağlama
açısı:
| a3cos |
(1) |
Bağlama açısının dik açıdan maksimum sapmasını belirlemek için ![]() nun krank açısı
nun krank açısı ![]() 12
ye göre türevi alınır sıfıra eşitlenir. Denklem (1) den:
12
ye göre türevi alınır sıfıra eşitlenir. Denklem (1) den:
| (2) |
Bağlama açısının maksimum veya minimum değeri ![]() 12
= 900 veya
12
= 900 veya ![]() 12
= 2700 olduğu konumlardır ve bu konumlarda
bağlama açısının maksimum veya minimum değeri:
12
= 2700 olduğu konumlardır ve bu konumlarda
bağlama açısının maksimum veya minimum değeri:
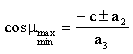 |
(3) |
dir. Eğer c Şekilde görüldüğü gibi, pozitif ise bağlama açısı ![]() 12
= 2700 iken dik açıdan maksimum sapar.
c negatif ise, en kritik bağlama açısı
12
= 2700 iken dik açıdan maksimum sapar.
c negatif ise, en kritik bağlama açısı ![]() 12
= 900 konumundadır.
12
= 900 konumundadır.
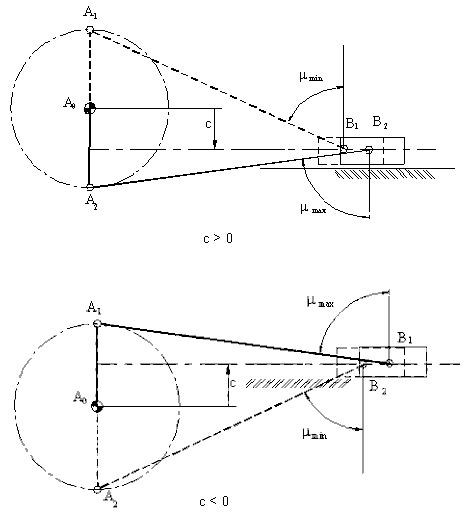
Eksantriklik sıfır ise (c=0), maksimum ve minimum bağlama açısı değerlerinin dik açıdan sapması eşit olup:
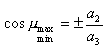 |
(4) |
Bir örnek olması açısından, pistonlu pompalarda, krank-biyel oranının genellikle ¼ den az bir oran olması istenilir. Bu ise bağlama açısının dik açıdan sapmasını 14.480 den az bir değerde tutacaktır. Santrik bir krank biyelde krank boyu istenilen stroka bağlı olduğundan (a2 = s/2), bu oranın elde edilmesi için biyel boyunun büyütülmesi, dolayısı ile mekanizmanın daha fazla hacim kapsamasını gerektirir.
Dört çubuk mekanizması için açıklanmış olan bağlama açısı problemi gibi, krank-biyel mekanizmaları içinde benzer bir problem ortaya konabilir:
| "Verilen bir strok, s, ve buna karşı gelen
krank dönme açısını ( |
Problemin yine iki kısmı bulunmaktadır. Birinci kısım, verilen strok
(s) ve karşı gelen kol dönme açısını (![]() )
sağlayan krank biyel mekanizmalarının bulunması ikinci kısım ise bu kinematik
özellikleri sağlayan krank-biyel mekanizmaları arasından bağlama açısı
dik açıdan en az sapma gösteren mekanizmanın bulunmasıdır.
)
sağlayan krank biyel mekanizmalarının bulunması ikinci kısım ise bu kinematik
özellikleri sağlayan krank-biyel mekanizmaları arasından bağlama açısı
dik açıdan en az sapma gösteren mekanizmanın bulunmasıdır.
Problemin birinci kısmı için strokun uzuv boyutları oranına bağlı olduğuna dikkat etmemiz gerekmektedir. Örneğin uzuv boyutlarını iki misli büyütür isek strok iki misli artacaktır. Bu dört çubuk mekanizmalarında kol dönme açıları için olmayan bir durumdur. Bu nedenle strok bir birim (s=1) olarak ele alınacak , sonuçta elde edilen krank ve biyel boyutları istenilen strok değeri ile çarpılarak gerçek olması gerekli boyutlar bulunacaktır.
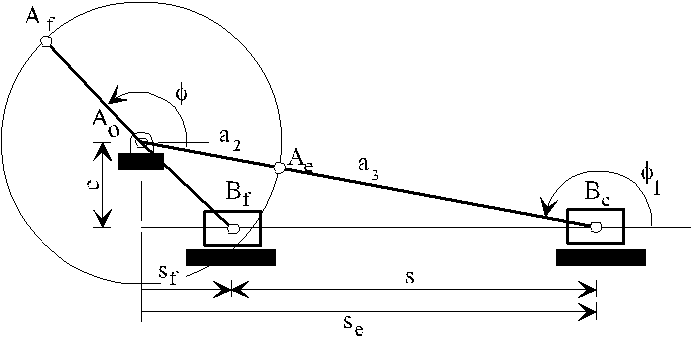
Şekilde gösterilmiş olan ölü konumlar için vektör devre denklemi:
| A0Be+BeAe+AeA0=0 | (5) |
| A0Bf+BfAf+AfA0=0 | (6) |
veya kompleks sayılar kullanılarak
| (7) | |
| (8) |
dır. Denklem (8) i denklem (7) den çıkarıp se-sf = s = 1 olarak alır isek:
| (9) |
olacaktır. ![]() ve
ve
![]() = a2/a3
olarak tanımlar isek, denklem (8):
= a2/a3
olarak tanımlar isek, denklem (8):
| (10) |
Olarak yazılabilir. Krankın tam bir dönme yapabilmesi için gerekli (yeterli
değil) |![]() |<
1 dir. Denklem (10) Z için çözüldüğünde:
|<
1 dir. Denklem (10) Z için çözüldüğünde:
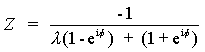 |
(11) |
elde edilir. Eğer ![]() bağımsız
parametre olarak kabul edilir ise,
bağımsız
parametre olarak kabul edilir ise, ![]() nın
değişik değerleri ile Z vektörünün uç noktası bir daire çizecektir (ka
dairesi). Bu, mekanizmanın ölü konumunda Ae
noktasının Be noktasına göre geometrik
yeridir. Sabit döner mafsal ekseni ise Z(1+
nın
değişik değerleri ile Z vektörünün uç noktası bir daire çizecektir (ka
dairesi). Bu, mekanizmanın ölü konumunda Ae
noktasının Be noktasına göre geometrik
yeridir. Sabit döner mafsal ekseni ise Z(1+![]() )
vektörü ile tanımlanan farklı bir daire (ko
dairesi) olacaktır. Her iki vektörde merkezi Be
den geçen ve reel ekseni piston öteleme ekseni ile çakışan sabit koordinat
eksenine göre çizilebilir. Şekilde bu daireler
)
vektörü ile tanımlanan farklı bir daire (ko
dairesi) olacaktır. Her iki vektörde merkezi Be
den geçen ve reel ekseni piston öteleme ekseni ile çakışan sabit koordinat
eksenine göre çizilebilir. Şekilde bu daireler ![]() =1600
durumu için çizilmiştir.Be den çizilen
herhangi bir doğru bu daireleri Ae ve
Ao noktalarında kesecektir.
=1600
durumu için çizilmiştir.Be den çizilen
herhangi bir doğru bu daireleri Ae ve
Ao noktalarında kesecektir.
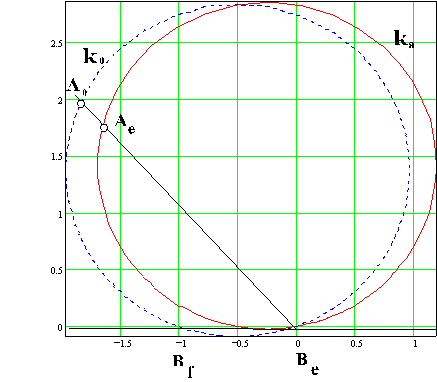
c, eksantriklik değeri ise:
BeAo=BeAe+AeAo
olan vektörün sanal bileşeni olarak elde edilecektir. Bir kompleks sayıdan kompleks eşleniği çıkarılır ise, sanal kısmın iki katı olacağından bu vektör denkleminden:
| (12) |
elde edilir. Bu denklemde önceden tanımlanmış olan Z ve ![]() parametreleri
kullanıldığında:
parametreleri
kullanıldığında:
| (13) |
olacaktır. Denklem (11) den elde edilen Z değeri kullanıldığında:
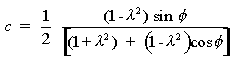 |
(14) |
olur. Bu durumda uzuv boyutları:
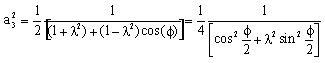 |
(15) |
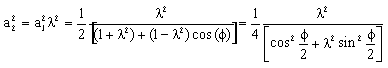 |
(16) |
olacaktır. (14-16) denklemleri kullanılarak verilen krank dönme açısı
ve stroku bir birim olan krank biyel mekanızmaları ![]() bağımsız parametresine göre elde edilmiştir ve sonsuz sayıda çözüm vardır.
İstenildiğinde
bağımsız parametresine göre elde edilmiştir ve sonsuz sayıda çözüm vardır.
İstenildiğinde ![]() parametresi yerine eksantriklik, krank veya biyel boyu bağımsız parametre
olarak kullanılabilir.
parametresi yerine eksantriklik, krank veya biyel boyu bağımsız parametre
olarak kullanılabilir.
Problemin Geometrik olarak çözümü için:
Örnek
Stroku s=120 mm, buna karşı gelen krank dönme açısı ![]() =1600
olan ve krank uzunluğunun biyel uzunluğuna oranı,
=1600
olan ve krank uzunluğunun biyel uzunluğuna oranı, ![]() =0.5
olan krank-biyel mekanizmasını bulun.
=0.5
olan krank-biyel mekanizmasını bulun.
Stroku bir birim alarak denklem (14), (15) ve (16) kullanılarak uzuv boyutları:
a2 = 0.47881, a3= 0.95762 ve c = 0.23523 olarak bulunur. s = 120 için ise a3= 114.91mm, a2 = 57.46mm ve c = 28.23mm olur.
Elde edilmiş olan bu mekanizma için minimum bağlama açısı değeri: ![]() min
= 41.790 dir.
min
= 41.790 dir.
Örnek
Örnekde strok ve krank dönme açısı olan ancak krank uzunluğunun biyel uzunluğuna göre oranı tanımlanmıyarak, eksantrikliği c = 20 mm olması istenilen krank biyel mekanizması boyutlarını bulalım.
Birim stok için c = 20/120 = 0.16667 dir. Denklem (10) u ![]() için
çözdüğümüzde:
için
çözdüğümüzde:
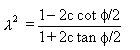 |
(13) |
olacaktır. c = 0.16667 ve ![]() =1600
için
=1600
için ![]() 2
= 0.325635 (
2
= 0.325635 (![]() =
0.5706) bulunur. (11) ve (12) numaralı denklemler kullanılarak a2=
0.48508 ve a3 = 0.85006 bulunur. s =
120 mm için c = 20mm , a2 = 58.21 mm
ve a3 = 102.01mm olacaktır. Bu krank
biyel mekanizması için minimum bağlama açısı değeri:
=
0.5706) bulunur. (11) ve (12) numaralı denklemler kullanılarak a2=
0.48508 ve a3 = 0.85006 bulunur. s =
120 mm için c = 20mm , a2 = 58.21 mm
ve a3 = 102.01mm olacaktır. Bu krank
biyel mekanizması için minimum bağlama açısı değeri: ![]() min
= 39.940. dikkat edilir ise, biyel uzunluğu
veya krank uzunluğu önceden verilir ise, benzer bir yöntem kullanılabilir.
min
= 39.940. dikkat edilir ise, biyel uzunluğu
veya krank uzunluğu önceden verilir ise, benzer bir yöntem kullanılabilir.
![]() =
=
![]() /2 iken
pozitif c değerleri için minimum bağlama açısı olacaktır ve değeri:
/2 iken
pozitif c değerleri için minimum bağlama açısı olacaktır ve değeri:
| (15) |
dir. Ayrıca, krankın tam dönme yapabilmesi için c+a <b veya c <b-a
olmalıdır. Sınır şart olarak (c = b-a) alındığında ![]() min
= 0 olur. Denklem (10), (11) ve (12) kullanılarak bu şartlar ölü konumlar
rasında krank dönme açısı
min
= 0 olur. Denklem (10), (11) ve (12) kullanılarak bu şartlar ölü konumlar
rasında krank dönme açısı ![]() için sınırlar getirecektir:
için sınırlar getirecektir:
| (16) |
ve ![]()
olur. Denklem 15 i ![]() ve
ve ![]() parametreleri ile yazdığımızda:
parametreleri ile yazdığımızda:
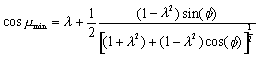 |
(17) |
olacaktır. ![]() bağımsız parametre olduğundan, en küçük bağlama açısı değerinin maksimum
olması için gerekli şart
bağımsız parametre olduğundan, en küçük bağlama açısı değerinin maksimum
olması için gerekli şart ![]() dır.
Bu türevi sıfır yapan
dır.
Bu türevi sıfır yapan ![]() değerine
değerine
![]() =
=
![]() opt
dersek, (17) denkleminin türevini alıp
opt
dersek, (17) denkleminin türevini alıp ![]() olur ise:
olur ise:
| t2Q3+(1-t2)Q2-(t4+t2+1)Q+(1+t2)=0 | (18) |
denklemi elde edilir. Bu denklemde Q = (![]() opt)2t2
ve t = tan(
opt)2t2
ve t = tan(![]() /2)
dir. Denklem (18) in üç kökü:
/2)
dir. Denklem (18) in üç kökü:
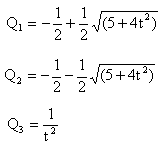 |
(19) |
Q pozitif olması gerektiğinden (= (![]() opt)2t2
daima pozitiftir), Q2 çözüm değildir.
Q3, değerinden
opt)2t2
daima pozitiftir), Q2 çözüm değildir.
Q3, değerinden ![]() =1/t2
elde edilir. Bu değere göre elde edilen mekanizmada bağlama açısının dik
açıdan sapması maksimumdur ( cos
=1/t2
elde edilir. Bu değere göre elde edilen mekanizmada bağlama açısının dik
açıdan sapması maksimumdur ( cos![]() min=1)
ve bu değerde optimum çözüm değildir. Q1
kökünden elde edilen
min=1)
ve bu değerde optimum çözüm değildir. Q1
kökünden elde edilen ![]() opt
değeri (1/t2, 1) aralığındadır ve bağlama
açısının dik açıdan sapmasını en aza indirir. Bu değer:
opt
değeri (1/t2, 1) aralığındadır ve bağlama
açısının dik açıdan sapmasını en aza indirir. Bu değer:
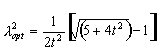 |
(20) |
dir ve aranılan çözüm tekdir.
Örnek
Stroku s=120 mm ve krank dönme açısı ![]() =1600
istenilmektedir. Bu kinematik özellikleri sağlayan ve en iyi bağlama açısı
özelliklerine sahip krank biyel mekanizmasını bulun.
=1600
istenilmektedir. Bu kinematik özellikleri sağlayan ve en iyi bağlama açısı
özelliklerine sahip krank biyel mekanizmasını bulun.
Denklem (20) den, ![]() opt=0.405185.
(14), (15) ve (16) numaralı denklemler kullanılarak birim strok için uzuv
boyutları: ac= 0.465542; a3=
1.14896 ; c= 0.377378 dir. s= 120 mm strok olduğunda ise:
opt=0.405185.
(14), (15) ve (16) numaralı denklemler kullanılarak birim strok için uzuv
boyutları: ac= 0.465542; a3=
1.14896 ; c= 0.377378 dir. s= 120 mm strok olduğunda ise:
a2= 55.87 mm; a3= 137.88 mm ; c= 42.81 mm
Sonuç Mekanizma Şekilde görülmektedir. Mekanizmanın minimum bağlama açısı
![]() min=
42.80 dir.
min=
42.80 dir.
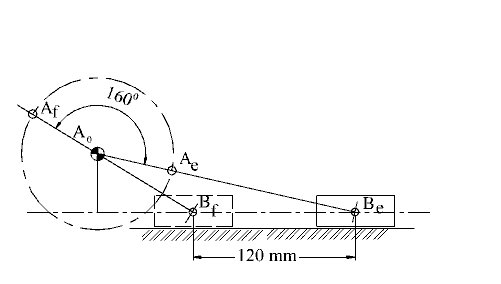
Elde edilen sonuç ölü konumlar arası kol dönme açısına göre bulunabilir.
Bu sonuçlar Kitapta Abak 2 de görülmektedir. Krank biyel mekanizması uzuv
boyutları (a2, a3,
c) ve ![]() opt
değeri ile birlikte en küçük bağlama açısı değeri mmin krankın ölü konumlar
arasında dönme açısına (
opt
değeri ile birlikte en küçük bağlama açısı değeri mmin krankın ölü konumlar
arasında dönme açısına (![]() )
göre verilmiştir. Abak 3 (Abak için kitaba bakınız) de ise tüm sonuçlar
eksantrikliğin stroka oranı (c/s) ve ölü konumlar artasında kalan krank
dönme açısına göre (
)
göre verilmiştir. Abak 3 (Abak için kitaba bakınız) de ise tüm sonuçlar
eksantrikliğin stroka oranı (c/s) ve ölü konumlar artasında kalan krank
dönme açısına göre (![]() )
verilmektedir (yatay eksen c/s olup lineer bir ölçekte değildir).
)
verilmektedir (yatay eksen c/s olup lineer bir ölçekte değildir).