8.3 Hareket Eğrileri
Uygulamada çok sayıda farklı hareket eğrileri kullanılmaktadır. Burada genel özellikleri açıklayan temel hareket eğrileri ele alınacaktır.
| 1. | Doğrusal Hareket: Doğrusal hareket eğrisi: |
s= C t
Kam için sabit açısal hız (![]() )
kabul edilir ise:
)
kabul edilir ise:
s= C![]() /
/![]() dır.
dır.
H= Strok boyu
![]() = kamın
tüm hareket sırasında döndüğü açı ise:
= kamın
tüm hareket sırasında döndüğü açı ise:
s=0 iken ![]() = 0 ve s = H iken
= 0 ve s = H iken ![]() =
= ![]() sınır
şartları kullanılarak:
sınır
şartları kullanılarak:
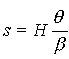
ve
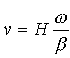
a=0, ancak başlangıç ve bitiş noktalarında
a=![]() olacaktır
olacaktır
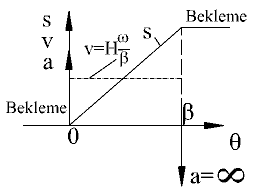
Şekilde Hareket, hız ve ivme eğrileri gösterilmiştir. Uç noktalarda ivmenin sonsuz olması bu tip bir eğrinin düşük hızlarda bile kullanılmasına müsaade etmemek-tedir. Ayrıca bu eğri kam eğrisi olarak çizildiğinde, süreksizlik hareket diyagramında görüldüğü gibi kam profilinde de olacaktır.
| 2. | Basit Harmonik hareket: |
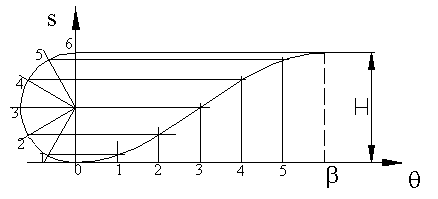
Tasarımı kolay ve sürekli bir hareket olmasından dolayı basit harmonik hareket bilhassa düşük veya orta hızlı kamlarda çok sıkca kullanılan bir harekettir. Geometrik olarak basit harmonik hareket Şekilde gösterildiği gibi, bir daire üzerinde bulunan noktaların s öteleme eksenine projeksiyonu ile elde edilir. Çapı toplam öteleme strokuna eşit yarım daire kam yükselme açısı bölümü kadar bölümlere ayrılır ve daire üzerinde alınan her noktanın dikey eksene projeksiyonu sırasında kamın belirlenen aralık kadar döndüğü öngörülür. Şekilden anlaşılacağı gibi, hareket başlangıç ve bitişte daha yavaş, orta noktalarda daha hızlı olacaktır. Bu tüm bekleme-hareket-bekleme için kullanılan eğrilerde aranılan özelliktir. Basit harmonik hareketin denklemi:
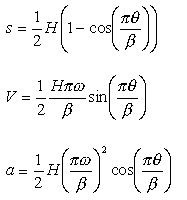
dir.
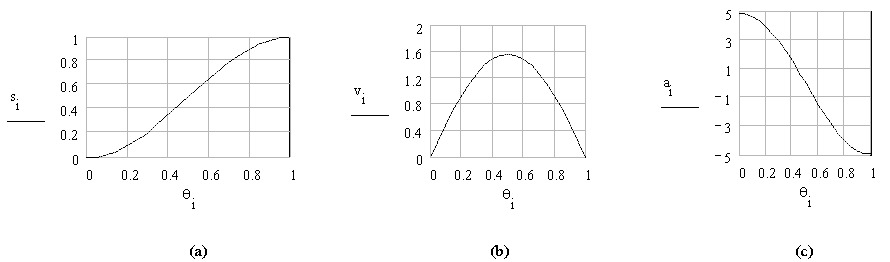
Hız ve ivme diyagramları Şekilde görülmektedir ve maksimum hız ve ivme değerleri:
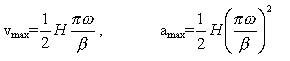
dir.
| 3. | Parabolik veya sabit ivmeli hareket: |
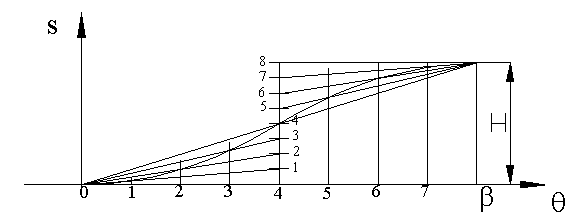
Parabolik harekette hareketin ilk yarısında izleyici sabit bir ivme ile hızlandırılırken ikinci yarısında sabit bir eksi ivme ile yavaşlatılır. Bu hareket eğrisini grafik olarak çizmek için izleyici yükselişi ile kamın dönme açılarını eşit sayılara bölmemiz gerekir. Yükseliş bölümlerini orta noktada bir dikey doğru üzerinde gösterelim. O başlangıç noktasından dikey doğru üzerinde bulunan 1,2,3 ve 4 noktalarına çizilen doğrular ile kam dönme açısı bölümlerinden çizilen dikey doğruların kesiştiği noktalar bu parabol üzeride bulunan noktalardır. Hareketin ikinci yarısı için O yerine O' noktası kullanılarak aynı işlem tekrarlanır.
İzleyicinin hareketi, hızı ve ivmesi kam dönme açısına göre:
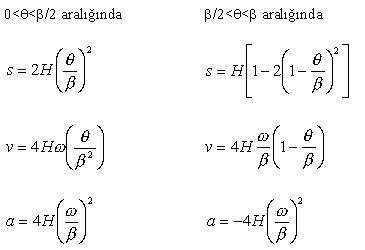
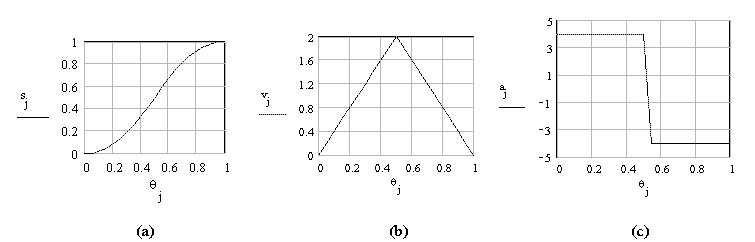
İvme her konumda belirli bir değer alırsa da, ivme değişimi (sadme) sonsuz olacaktır. Hareket, hız ve ivme diyagramları Şekilde gösterilmektedir.
| 4. | Sikloid Hareket Eğrisi: |
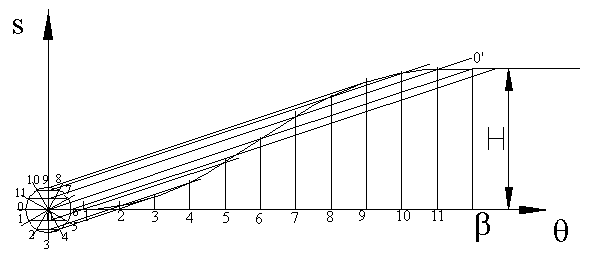
Eğer bir daire bir doğru üzerinde yuvarlanır ise, daire çemberi üzerinde
bir nokta sikloid eğrisini çizer. İzleyicide sikloid hareketi elde etmek
için çevresi H veya çapı H/![]() olan, merkezi ise OO' doğrusu üzerinde bulunan daire çizilir. Daire çemberi
ve kam yükseliş açısı aynı sayıda eşit aralıklara bölünür. Bu daire üzerinde
bulunan bir noktadan (örneğin 1 noktası) çizilen yatay doğrunun dikey
ekseni kestiği noktadan OO' ye paralel çizilen doğru ile aynı noktaya
karşı gelen yatay eksen üzerindeki noktadan (1 noktası) çizilen dikey
doğrunun kesiştiği nokta yükselme eğrisi üzerinde bir noktayı belirler.
Analitik olarak hareket, hız ve ivme eğrileri :
olan, merkezi ise OO' doğrusu üzerinde bulunan daire çizilir. Daire çemberi
ve kam yükseliş açısı aynı sayıda eşit aralıklara bölünür. Bu daire üzerinde
bulunan bir noktadan (örneğin 1 noktası) çizilen yatay doğrunun dikey
ekseni kestiği noktadan OO' ye paralel çizilen doğru ile aynı noktaya
karşı gelen yatay eksen üzerindeki noktadan (1 noktası) çizilen dikey
doğrunun kesiştiği nokta yükselme eğrisi üzerinde bir noktayı belirler.
Analitik olarak hareket, hız ve ivme eğrileri :
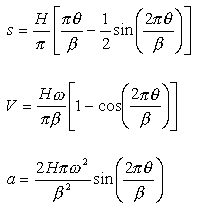
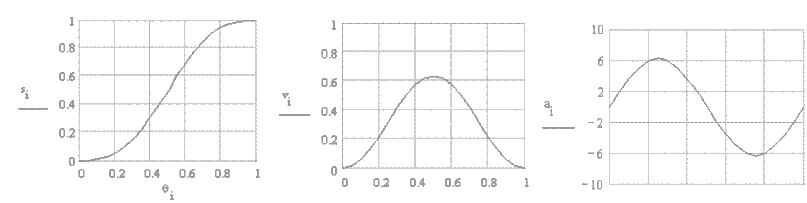
Hareket, hız ve ivme diyagramları
Şu ana kadar açıklanmış olan eğriler arasında sikloid hareket eğrisi en iyi dinamik özellikere sahip kam sistemini verebilecektir. İvme her noktada sınırlı olup başlangıç ivmeside sıfırdır. Bu en az titreşim, gürültü oluşturan bir kam sistemini vereceğinden genellikle tavsiye edilir. Ancak bu özelliklere erişilebilmesi için kamın çok hassas imal edilmesi şarttır.
| 5. | Doğru ve Daire Yayı - Birleşik eğriler: |
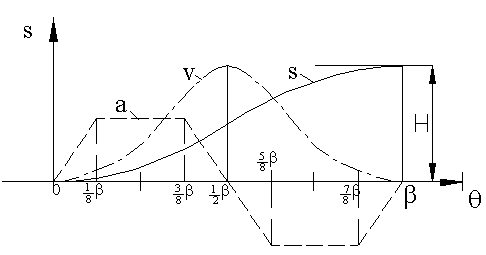
Doğrusal hareket eğrisinde, başlangıç ve bitiş noktaları sonsuz ivme olduğundan dolayı uygulamada sorun yaratacaktır. Başlangıç ve bitiş noktalarında sonsuz ivmeyi önlemek için başlangıç ve bitiş bir daire yayı, arada ise bu iki daire yayına teğet bir doğru çizilerek elde edilen yükseliş eğrisinde hareket ve hareketin birinci türevi sürekli olacak, ivme ise her noktada sonlu bir değer alacaktır. Aşağıdaki şekilde gösterildiği gibi, genel olarak daire yayı yarı çapı yükselme mesafesine (H) eşit alınır ise de, farklı bir çapta kullanılabilir.
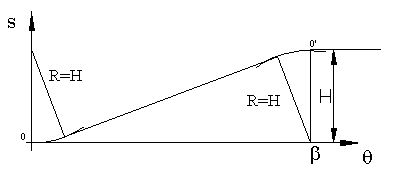
Kalkış sırasında belirli bir aralıkda sabit bir hız elde edilebilmesi için doğrusal hareket eğrileri bir çok uygulama için gereklidir. Hareketin sürekliliğini sağlamak için ise, başlangıç ve bitiş noktalarında daire yayı kullanılabileceği gibi, harmonik haraketin, parabolik hareketin veya sikloid hareketin yarısı bu doğruyu başlangıç ve bitiş noktalarına sıfır eğim ile bağlayabilir.
Örnek 1 :
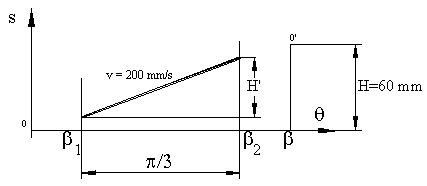
50 devir/dakika açısal hız ile dönen bir kam mekanizmasında, izleyicinin ilk olarak sabit ivme ile 200 mm/s hıza çıkmasını, 600 bu sabit hız ile hareket etmesini ve sonra sabit ivme ile toplam 60 mm yükseliş yaptıktan sonra beklemeye girmesi istenmektedir.
Bu yükseliş eğrisini, hızını ve ivmesini belirleyelim.
Şekilde görüldüğü gibi, yükseliş eğrisi üç kısımdan oluşacaktır. 0<![]() <
<![]() 1
aralığında sabit ivme,
1
aralığında sabit ivme, ![]() 1<
1<![]() <
<![]() 2
aralığında sabit hız ve
2
aralığında sabit hız ve ![]() 2<
2<![]() <
<![]() aralığında ise yine sabit ivme ile durmadır. Kamın açısal hızı
aralığında ise yine sabit ivme ile durmadır. Kamın açısal hızı ![]() =50*
=50*![]() /30=
5.238 radyan/s olduğuna göre
/30=
5.238 radyan/s olduğuna göre ![]() /3
aralığı,
/3
aralığı, ![]() t=0.2
saniyede alınacak 200 mm/s hızla yükseliş H'=200*0.2= 40 mm olacaktır.
Diğer iki aralıkta toplam yükselme 20 mm dir. Başlangıç ve bitiş ivmelenmeleri
sırasında aynı yükseliş olduğu kabul edilir ise, her iki kısımda 10'ar
mm yükseliş alınabilir. Dikkat edilir ise sabit ivme sırasında kamın dönme
açısı belirli değildir (mümkün olduğunca artırılması amaçlanmalıdır).
t=0.2
saniyede alınacak 200 mm/s hızla yükseliş H'=200*0.2= 40 mm olacaktır.
Diğer iki aralıkta toplam yükselme 20 mm dir. Başlangıç ve bitiş ivmelenmeleri
sırasında aynı yükseliş olduğu kabul edilir ise, her iki kısımda 10'ar
mm yükseliş alınabilir. Dikkat edilir ise sabit ivme sırasında kamın dönme
açısı belirli değildir (mümkün olduğunca artırılması amaçlanmalıdır).
0<![]() <
<![]() 1
aralığı sırasında sabit ivme için parabolik hareket olacaktır.
İkinci dereceden hareket eğrisi:
1
aralığı sırasında sabit ivme için parabolik hareket olacaktır.
İkinci dereceden hareket eğrisi:
s=c0+c1![]() +c2
+c2![]() 2
2
şeklinde yazılabilir. Sınır şartlar olarak ![]() =0
iken s=0 ve
=0
iken s=0 ve ![]()
![]() =
=![]() 1
iken ise, s=10 mm ve
1
iken ise, s=10 mm ve ![]() olmalıdır.
olmalıdır.
![]() =0 şartları
kullanıldığında c0=c1=0
elde edilir.
=0 şartları
kullanıldığında c0=c1=0
elde edilir. ![]() =
=![]() 1
de konum ve hız şartlarından ise:
1
de konum ve hız şartlarından ise:
c2![]() 12
= H1 = 10mm
12
= H1 = 10mm
2c2![]() 1
1![]() = 200mm/s
= 200mm/s
dir. bu denklemlerden ![]() 1
=
1
= ![]() /6 (300)
ve c2=360/
/6 (300)
ve c2=360/![]() 2
olarak elde edilir.
2
olarak elde edilir.
![]() 2<
2<![]() <
<![]() aralığında yine sabit ivme olacağından aynı ikinci derece eğri kullanılacak
ve sınır şartlar
aralığında yine sabit ivme olacağından aynı ikinci derece eğri kullanılacak
ve sınır şartlar ![]() =
=
![]() 2=
2=
![]() /2 için
s=50 mm,
/2 için
s=50 mm, ![]()
![]() =
=![]() için ise s=H=60 mm ve
için ise s=H=60 mm ve ![]() olacaktır.
Bu şartlar kullanıldığında
olacaktır.
Bu şartlar kullanıldığında ![]()
![]() =
=![]() -
-![]() 2
=
2
= ![]() /6,
/6,
![]() olarak
bulunur. Bu durumda yükseliş eğrisi denklemleri:
olarak
bulunur. Bu durumda yükseliş eğrisi denklemleri:
0<![]() <
<![]() /6
için
/6
için
![]()
![]() /6<
/6<![]() <
<![]() /2
için
/2
için
![]()
![]() /2<
/2<![]() <2
<2![]() /3
için
/3
için
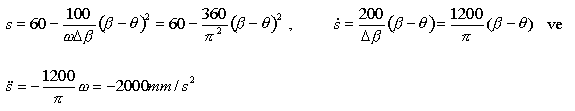
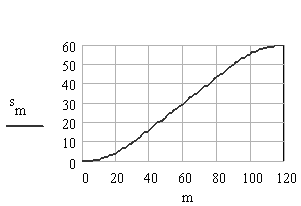
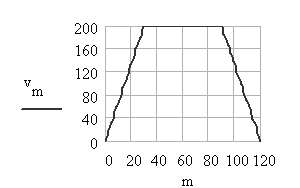
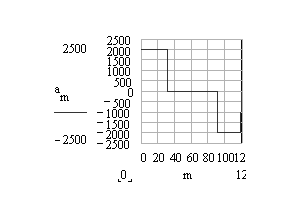
Hareket, hız ve ivme eğrileri
| 6. | Trapezoid ivme eğrisi: |
Açıklanmış olan parabolik veya sabit ivmeli harekette başlangıç ve bitiş noktalarında ivmenin bir basamak şeklinde değişmesi yerine, ivmenin zamana göre türevinin sonsuz olmasını önlemek için diktörtgen şeklinde olan ivme eğrisinin dikey kenarlarını meyillendirerek trapez şeklinde bir ivme diyagramı elde edilebilir (Şekil ). Genellikle ivmenin düzgün değiştiği bu kısım yükselme açısının 1/8 i kadar alınır. Kalan aralıkda sabit ivmeli hareket vardır. Trapezoid ivme eğrisi:
| a. | Parabolik eğriye göre titreşim ve gürültüsü daha az , aşınma ve şok etkisi daha uygun kam sistemi ile sonuçlanır. |
| b. | Üçüncü derece hareket veya sikloidal harekete göre daha küçük kam ebatları ve daha düşük maksimum ivme değerleri elde edilir. |
| c. | Bağlama açısı aynı taban dairesi için üçüncü derece hareket eğrisine nazaran daha iyidir. |
Bu nedenlerden dolayı trapezoid ivme eğrisi (veya bu eğrinin daha iyileştirilmiş şekilleri) bilhassa otomotiv sanayiinde en fazla kullanılan eğridir (İleri tasarım şartlarında bu trapez ivme diyagramında köşelerinde sürekliliğin sağlanması düşünülmelidir).
| 7. | Üçüncü Derece Hareket Eğrisi (#1): |
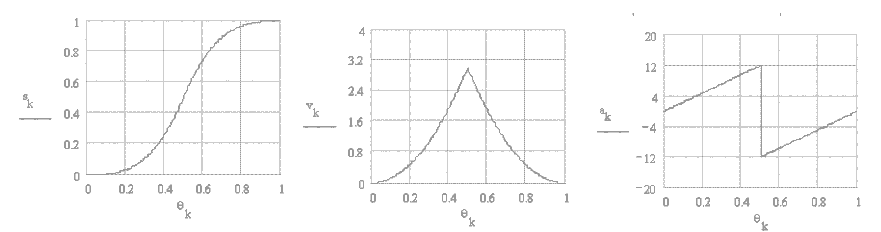
İvmenin sabit olmayıp düzgün olarak değişmesi istenilir ise hareket üçüncü dereceden olacaktır. Birinci tip (#1) üçüncü derece hareket eğrisinde ivmenin zamana göre değişimi pozitifdir. Bu nedenle eğri iki üçüncü derece eğrinin birleşiminden elde edilir. Hareketin başlangıç ve bitişinde ivmenin sıfır olması avantajlı isede, orta noktada ivmenin sürekli olmayışı uygulamada sorunlar yaratır (sadme sonsuz olacaktır). Bu nedenle tavsiye edilmemektedir. Analitik olarak hareket, hız ve ivme denklemleri:
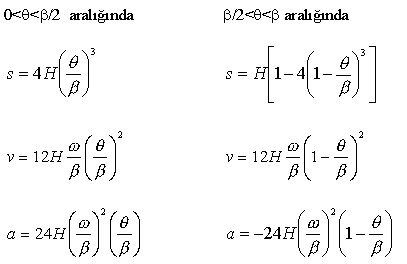
| 8. | Üçüncü Derece Hareket Eğrisi (#2): |
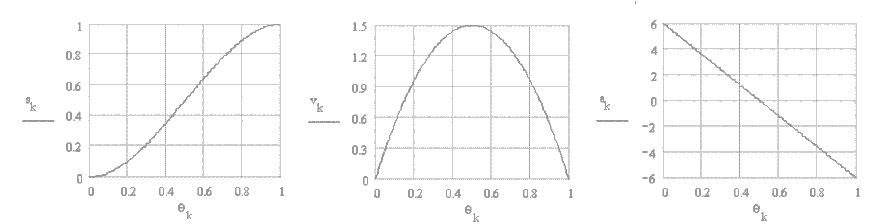
İkinci tip üçüncü derece hareket eğrisi ise tek bir eğriden oluşmuştur ve süreklidir. Bu eğriye aynı zamanda 2-3 polinomu da denmektedir. Hareket, hız ve ivme eğrileri Şekilde verilmiştir. Analitik olarak denklemler:
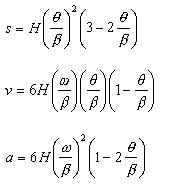
| 9. | Çift Harmonik Hareket eğrisi: |
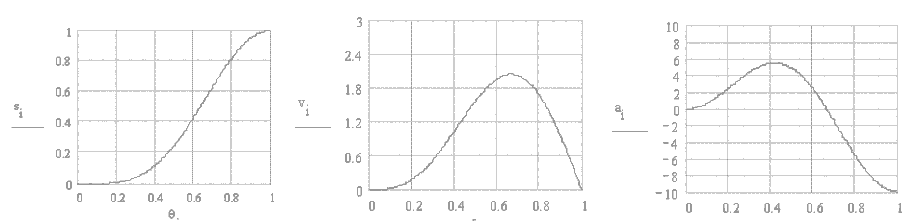
Bu eğri iki harmonik hareketin farkından oluşmaktadır. Şu ana kadar elde edilmiş eğriler simetrik iken, bu eğri simetrik değildir (Şekil). Bu nedenle Bekleme-Hareket veya Bekleme-Hareket-Doğrusal Hareket gibi durumlarda kullanımı daha uygundur. Hareket, hız ve ivme denklemleri:
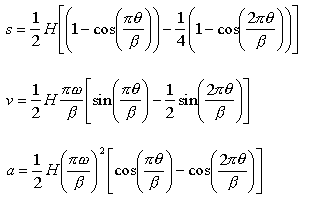
| 10. | Polinom hareket eğrileri: |
Pratikte kullanılan temel hareket eğrileri genel olarak yukarıda açıklanmış olan hareket eğrileridir. Ancak yüksek hızlarda ve özel uygulamalarda değişik hareket eğrileri kullanılabilir. Bu eğrilerde dördüncü türeve kadar süreklilik aranmaktadır. Çok sayıda harmoniklerden oluşan hareket eğrilerinin titreşim açısından uygun olmadığı görülmüştür. Çeşitli çalışmalarda sabit ivme - parabolik hareket eğrisini trapezoid iv-mede olduğu gibi, düzeltme yolları araştırılmıştır (örneğin ilk 1/8 de doğrusal ivme yerine harmonik ivme gibi). Bir başka yaklaşım ise çeşitli derecede bir polinomların hareket eğrisi olarak kullanılmasıdır.
Bir polinomun genel denklemi:
s=c0+c1![]() +c2
+c2![]() 2+...+cn
2+...+cn![]() n
n
dir. Burada:
s= izleyici hareketi
![]() =
kam dönme açısı
=
kam dönme açısı
ci = sabit değerler (i= 0,,,n)
n= polinom derecesi
Bu polinomun kam açısı ![]() kadar döndüğünde izleyiciyi H kadar yer değiştirmesi istendiği gibi başlangıç
ve bitişte bekleme olduğundan bu konumlarda izleyicinin hızı, ivmesi sıfır
olması gerekir (bu şekilde, bekleme ile başlayıp biten harekette süreklilik
sağlanabilir):
kadar döndüğünde izleyiciyi H kadar yer değiştirmesi istendiği gibi başlangıç
ve bitişte bekleme olduğundan bu konumlarda izleyicinin hızı, ivmesi sıfır
olması gerekir (bu şekilde, bekleme ile başlayıp biten harekette süreklilik
sağlanabilir):
![]() =0
iken
=0
iken ![]() =
=![]() iken
iken
s=0 s=H
![]() =0
=0
![]() =0
=0
![]() =0
=0 ![]() =0
=0
olması gerekir. Bu altı sınır şartın sağlanabilmesi için polinomda altı sabit bulunmalı, yani polinom beşinci dereceden olmalıdır. Bu polinom ve türevleri:
s=c0+c1![]() +c2
+c2![]() 2+c3
2+c3![]() 3+c4
3+c4![]() 4+c5
4+c5![]() 5
5
![]() /
/![]() =c1
+2 c2
=c1
+2 c2![]() + 3c3
+ 3c3![]() 2
+4c4
2
+4c4![]() 3
+5c5
3
+5c5![]() 4
4
![]() /
/![]() =2
c2 + 6c3
=2
c2 + 6c3![]() +12c4
+12c4![]() 2
+20c5
2
+20c5![]() 3
3
olacaktır. Yukarıda verilmiş olan sınır şartlar kullanıldığında:
0 = c0
H = c0
+ c1![]() + c2
+ c2![]() 2
+ c3
2
+ c3![]() 3
+c4
3
+c4![]() 4
+c5
4
+c5![]() 5
5
0= c1
0= c1
+ 2c2![]() + 3c3
+ 3c3![]() 2
+4c4
2
+4c4![]() 3
+5c5
3
+5c5![]() 4
4
0=2c2
0=2 c2
+ 6c3![]() +12c4
+12c4![]() 2
+20c5
2
+20c5![]() 3
3
c0=c1=c2=0 değerleri diğer denklemlerde kullanılır ise, diğer üç denklem bilinmeyen diğer üç kat sayı için çözüldüğünde:
![]()
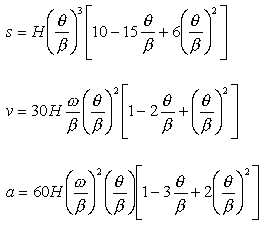
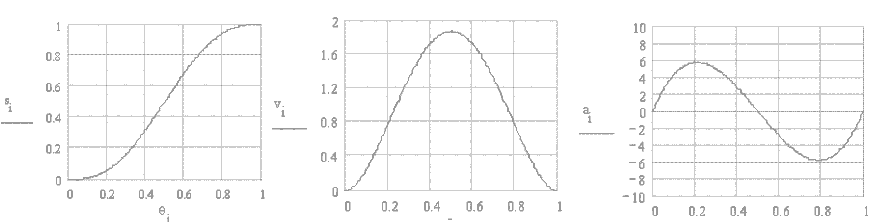
Bu polinom literatürde 3-4-5 polinomu olarak bilinmektedir. Yüksek dereceli
polinomların hareket eğrilerinde başlangıç ve bitiş noktalarında gittikçe
daha az izleyici hareketi olacaktır. Bu tür eğrilerin kamda gerçekleştirilebilmesi
için çok hassas imalat gereklidir. Örneğin başlangıç ve bitiş noktalarında
üçüncü türevinde sıfır olması şartı getirilir ise (![]() =0),
sınır şartı sekize çıkacak ve yedinci derece bir polinom ile sınır şartlar
sağlanacaktır. Ancak iki uç noktada hareketin az olması, ara konumlarda
hızın ve ivmenin daha yüksek olmasını gerektirecektir. Bu nedenlerden
dolayı, kullanılacak eğriye hem imalat ve hemde uygulamanın gerektirdiği
şartlar birlikte göz önüne alınarak karar verilmelidir.
=0),
sınır şartı sekize çıkacak ve yedinci derece bir polinom ile sınır şartlar
sağlanacaktır. Ancak iki uç noktada hareketin az olması, ara konumlarda
hızın ve ivmenin daha yüksek olmasını gerektirecektir. Bu nedenlerden
dolayı, kullanılacak eğriye hem imalat ve hemde uygulamanın gerektirdiği
şartlar birlikte göz önüne alınarak karar verilmelidir.
Örnek 2 :
Aşağıda verilmiş olan hareketi sağlayan kamın 3600si için hareket diyagramını verecek denklemleri bulun, hareket eğrisini çizin.
Sikloidal Hareket ile 1200 de 40 mm yükseliş
300 kam dönüşü sırasında bekleme
900 kam dönmesi ile 20 mm geri dönüş (basit harmonik hareket)
300 kam dönüşü sırasında bekleme
600 kam dönmesi ile 20 mm geri dönüş (parabolik hareket).
(Genel olarak bir kamda tüm hareketler için uygulama ve imalat şekline bağlı olarak tek hareket tipi seçilir. Burada değişik kam eğrisi örneklerini göstermek için üç değişik hareket eğrisi seçilmiştir)
İstenilen hareket eğrileri, verilen yükseliş ve krank dönme açılarına
göre (hepsi yükseliş eğrisi olarak ve hepsi ![]() =00
de yükselişe başlayacak şekilde):
=00
de yükselişe başlayacak şekilde):
Sikloid hareket (H=40 mm, ![]() =2
=2![]() /3) s=(20/
/3) s=(20/![]() )(3
)(3![]() -sin3
-sin3![]() )
)
Basit harmonik hareket (H=20 mm, ![]() =
=![]() /2) s=10(1-cos2
/2) s=10(1-cos2![]() )
)
Parabolik hareket (H=20 mm, ![]() =
=![]() /3)
/3)
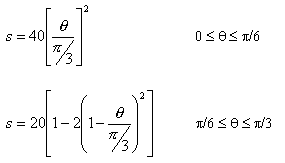
Bu denklemleri uygun bölgeye taşır, geri dönüş eğrileri haline getirirsek kamın 3600 dönmesi sırasında izleyici hareket eğrisini elde edebiliriz:
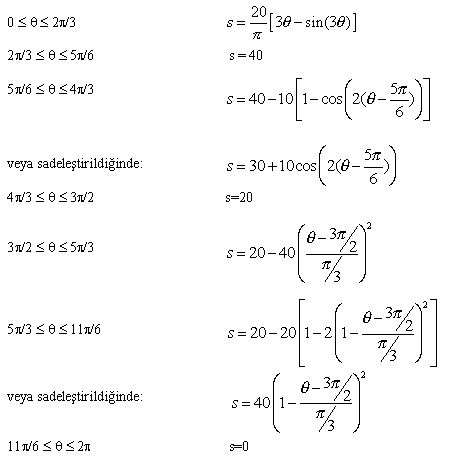
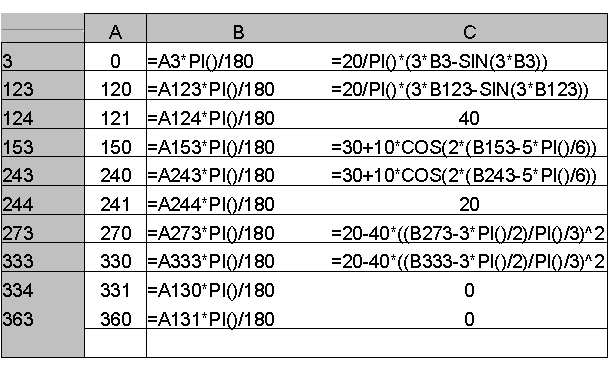
Hareket eğrisi kamın tam bir devri için hareket eğrisi Excel programı kullanılarak hesap edilmiş ve çizilmiştir. Şekilde Excel tablosunun belirli satırlarında yazılmış olan formüller gösterilmektedir. A kolonunda hücrelere 3 den 363 e kadar bir derece aralıklarla kam açısı, B kolonunda aynı satırlarda bulunan hücrelerde ise bu açının radyan olarak değeri bulunmaktadır. C kolonunda ise örneğin 3 ile 123 satırları arasında hücrelere sikloid eğri formülü yazılmıştır (formül C3 hücresine yazıldıktan sonra C4-C123 arasındaki hücrelere kopyalanır. Burada ara satırlar gösterilmemiştir). 124 ile 152 satırları arasında beklemeden dolayı C sütünunda hücrelere sadece 40 değeri girilmiştir. Benzer işlem geri dönüş eğrileri içinde tekrarlanmıştır. Sonuçta elde edilen değerler Şekilde Excel grafik komutu ile elde edilen hareket diyagramıdır (aralık istenir ise 0.10 olarakda alınabilir).
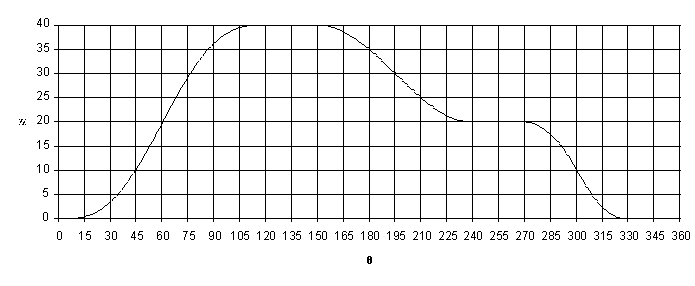
Elde edilmiş olan bu hareket eğrisi denklemi ile istenilen sıklıkta ve istenilen hassasiyette hareket eğrisi değerleri elde edilebilecektir. İleride kam profili elde edilmesi sırasında bunun önemi anlaşılacaktır.