6.2 Planet Dişli Sistemleri

Basit dişli zincirlerinde uzvun bir kinematik elemanı dişli çifti oluşturuyor ise, diğer kinematik elemanı sabit uzuv ile döner mafsal oluşturması gerekmekte idi. Eğer diğer kinematik eleman hareketli bir uzuv ile döner mafsal oluşturuyor ise, elde edilen zincire planet dişli sistem diyeceğiz. Dikkat edilir ise, şekil kapalı dişli çiftinin oluşturulabilmesi için dairesel dişlilerin eksenleri arasında uzaklığın sabit bir uzaklık olması şarttır. Planet dişli sistemlerde bazı dişlilerin dönme merkezi sabit olmayacak ancak diş eksenleri arasında uzaklık bir kol aracılığı ile sabit kalacaktır. Bu durumda dönen uzuvlar arasında hız oranı ile dişli oranı basit dişli sistemlerde olduğu gibi eşit değildir. Planet dişli sistemleri küçük hacimde yüksek hız oranları elde etmeyi sağlayan önemli bir sistemdir. Diferansiyel kutularında, otomatik vitesli arabalarda, çeşitli alet ve cihazda, iş makinalarında, vinçlerde kullanılmaktadır.

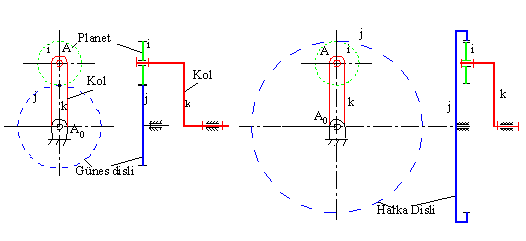
Planet dişli sistemin tek bir dişli çiftten oluşan en basit şekli aşağıdaki şekilde görülmektedir. Kol (k uzvu) A₀ dan geçen bir eksen etrafında dönebilmektedir. j uzvu (genellikle bu uzva, dıştan dişli oluşturuyorsa güneş dişli, içten dişli oluşturuyor ise halka dişli denir) bir döner mafsal ile sabit uzva A₀ noktasından bağlanmıştır. Planet dişli olarak adlandırılan i uzvu ise, j uzvu ile dişli çift oluştururken, kola A noktasından bir döner mafsal ile bağlıdır. Sistem bu şekli ile iki serbestlik derecelidir.

Şematik gösterimde planet dişli sistemlerinin yan görünümü tercih edilir.

Planet dişli üzerinde bulunan her hangi bir noktanın konumunun koordinatları parametrik olarak:

x = a₁cosθ + a₂cos(Rθ)

y = a₁sinθ + a₂sin(Rθ)

veya karmaşık sayılar ile:

z = a₁e^iθ + a₂e^iRθ

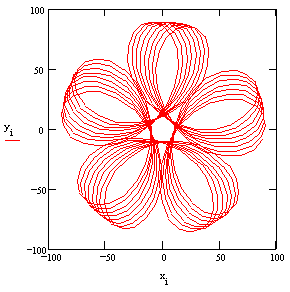
denklemi ile ifade edilebilir. Bu denklemde θ bağımsız değişkendir ve genellikle kolun dönme açısıdır. a₁, a₂ ve R sabit değerlerdir (R diş sayılarının oranına bağlıdır, a₁ ve a₂ ise kol uzunluğu ve incelenen noktanın planet dönme merkezi, A noktasına uzaklığıdır). Yörünge genellikle çok ilginç eğriler oluşturur. Bu eğriler episkloid ve hiposikloid eğrilerdir. Planet dişli sistemlerin bu özelliğinden dolayı episikloid dişli sistem olarakda adlandırılırlar. Aşağıda bir örnek gösterilmiştir. Bu tür hareketler, örneğin karıştırıcılarda karıştırıcı kanadın her defada değişik bir nokta ile temas etmesi ve tüm hacmi taraması için kullanılır.Diş oranlarına ve planet dişli üzerinde seçilen noktanın geometrik yerine göre bu eğri bir elips olabileceği gibi, doğruda olabilir.

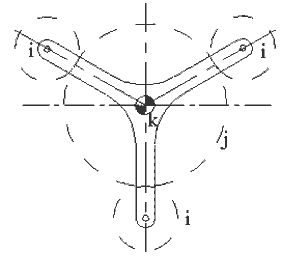
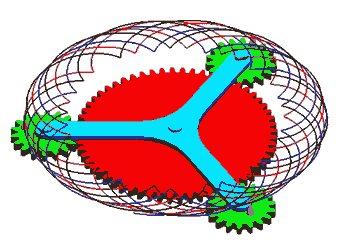
Büyük yük altında çalışan planet dişli sistemlerde yükü dengelemek ve bölmek için aynı kola mafsallanmış ve aynı güneş dişli ile dişli çift oluşturan çok sayıda planet dişli bulunabilir. Genellikle planet dişliler eşit aralıklarla güneş dişli çevresine yerleştirilmiştir. Üç planet dişlili bir örnek Şekilde görülmektedir. Bu planet dişlilerin kinematik analizleri sırasında tek bir planet dişli göz önüne alınması gerekir.

Planet dişli sistemlerin hareket analizi için önceden açıklanmış olan bağıl hareket kavramı göz önüne alınmalıdır. Planetin hareketi iki hareketin toplamı olarak düşünülebilir. Bunlardan birisi planet dişlinin A merkezli dönme hareketidir. İkinci hareket ise, A noktası sabit olmadığından, planet dişli üzerinde bulunan A noktasının kol üzerinde hareketidir.

Aşağıda gösterilmiş olan planet dişli sistemini ele alalım. P noktası iki dişli elemanının temas noktasıdır ve sadece yuvarlanma olduğundan P_i ve P_j noktalarının hızları aynıdır. Öyle ise:

v_Pi = v_Pj = v_A + v_P/A

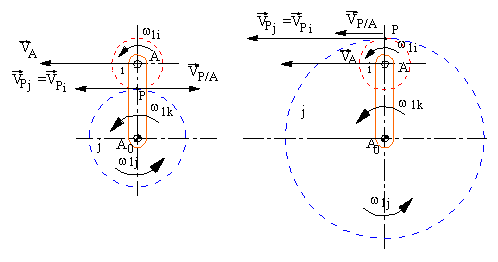
Açısal hızları saat yelkovanına ters yönde olduklarında pozitif kabul edelim. Hız bileşenlerinin yönleri aynı doğrultuda olacaklarından hızlar pozitif veya negatif olacak ve vektörel hız denklemi skaler toplam olarak ele alınabilecektir. Hız bileşenleri açısal hız ve dişli yarıçapları ile yazıldığında

v_pj = v_pi = ω_1j r_j

v_A = ω_1k(r_j ± r_i)            (+ dış dişli, − iç dişli olur ise)

v_P/A = ±ω_1ir_i                  (− dış dişli, + iç dişli olur ise)

Bu denklemlerde r_i ve r_j şekilde görüldüğü gibi dişli bölüm dairesi yarıçapıdır. Bu durumda hız denklemi:

ω_1jr_j = ω_1k(r_j \displaystyle \mp r_i) ± ω_1ir_i

olur. veya:

\displaystyle \mp \frac{{{{\text{r}}_{\text{i}}}}}{{{{\text{r}}_{\text{j}}}}}=\frac{{{{\text{ω}}_{{\text{1j}}}}-{{\text{ω}}_{{\text{1k}}}}}}{{{{\text{ω}}_{{\text{1i}}}}-{{\text{ω}}_{{\text{1k}}}}}}          (− dış dişli, + iç dişli olur ise)

denklemin sol tarafı için dişli teorisi kullanılarak:

\displaystyle \mp \frac{{{{\text{r}}_{\text{i}}}}}{{{{\text{r}}_{\text{j}}}}}=\mp \frac{{{{\text{d}}_{\text{i}}}}}{{{{\text{d}}_{\text{j}}}}}=\mp \frac{{{{\text{T}}_{\text{i}}}}}{{{{\text{T}}_{\text{j}}}}}={{\text{R}}_{{\text{ij}}}}

yazılabilir. Dikkat edilir ise R_ij diş sayısı oranıdır ve basit dişli sistemlerde olduğu gibi, o uzuvların hız oranı değildir. Dış dişli çift için R_ij = −T_i/T_j ve iç dişli için R_ij = +T_i/T_j basit dişli sistemler için tanımlandığı gibidir. Ayrıca denklem incelendiğinde diş sayısı oranı hız oranına eşit değilsede, ω_1j − ω_1k teriminin ω_1i − ω_1k terimine oranıdır. Bu terimler ise, düzlemsel harekette i ve j uzuvlarının kola (k uzvu) göre bağıl hızlarıdır. Yani:

ω_kj = ω_1j − ω_1k            (j uzvunun k uzvuna göre bağıl hızı)

ω_ki = ω_1i − ω_1k            (i uzvunun k uzvuna göre bağıl hızı)

Öyle ise:

\displaystyle {{\text{R}}_{{\text{ij}}}}=\frac{{{{\text{ω}}_{{\text{kj}}}}}}{{{{\text{ω}}_{{\text{ki}}}}}}=\frac{{{{\text{ω}}_{{\text{1j}}}}-{{\text{ω}}_{{\text{1k}}}}}}{{{{\text{ω}}_{{\text{1i}}}}-{{\text{ω}}_{{\text{1k}}}}}}

Bazı durumlarda bu denklemi:

ω_1iR_ij + ω_1k(1 − R_ij) − ω_1j = 0

yazmak doğru olacaktır. Eğer diş sayısı veya dişli çapları biliniyor ise, denklemde üç açısal hız değişkeni vardır (ω_1j, ω_1i, and ω_1k). Eğer iki açısal biliniyor ise, üçüncü açısal hız bulunabilir.

Basit dişli sistemlerde hız oranı (N_ij = ω_1j/ω_1i ) ve dişli sayısı oranı (R_ij = T_i/T_j) aynıdır. Bu nedenle R_ij sembolü her iki oran için kullanılmıştır. Planet dişli sistemler için bu iki oran farklı olacağından, R_ij sembolü dişli çifti oluşturan iki dişlinin diş sayısı oranı olarak (T_i/T_j ) kullanılacak, uzuvlar arasında hız oranı ise N_ij sembolü ile gösterilecektir. Sadece basit dişli sistemler için R_ij = N_ij geçerlidir.

Örnek:

Basit bir örnek olarak Şekilde görülen planet dişli sistemini ele alalım. Güneş dişlide 60 diş ve planet dişlide 22 diş bulunmaktadır. Kol 100 dev/dk hızla saat yelkovanına ters yönde güneş dişli ise 150 dev/dk saat yelkovanı (SY) yönünde dönmektedir. Saat yelkovanına ters (SYT) yönde dönmeyi pozitif kabul ederek:

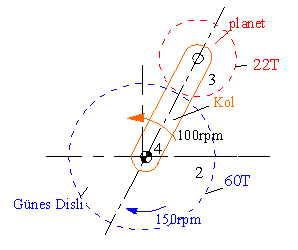
\displaystyle -\frac{{60}}{{22}}=\frac{{{{\text{ω}}_{{\text{1j}}}}-100}}{{150-100}}

veya:

ω₁₃ = 250×60/22 + 100 = 782 dev/dk (SYT)

Örnek:

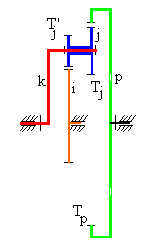
İkinci bir örnek olarak da yukarıda görülen planet dişli sistemini ele alalım. Diş oranı olarak:

i ve j uzuvları arasında \displaystyle {{\text{R}}_{{\text{ij}}}}=\frac{{{{\text{ω}}_{{\text{kj}}}}}}{{{{\text{ω}}_{{\text{ki}}}}}}=\frac{{{{\text{ω}}_{{\text{1j}}}}-{{\text{ω}}_{{\text{1k}}}}}}{{{{\text{ω}}_{{\text{1i}}}}-{{\text{ω}}_{{\text{1k}}}}}}

p ve j uzuvları arasında \displaystyle {{\text{R}}_{{\text{pj}}}}=\frac{{{{\text{ω}}_{{\text{kj}}}}}}{{{{\text{ω}}_{{\text{kp}}}}}}=\frac{{{{\text{ω}}_{{\text{1j}}}}-{{\text{ω}}_{{\text{1k}}}}}}{{{{\text{ω}}_{{\text{1p}}}}-{{\text{ω}}_{{\text{1k}}}}}}

i ve p uzuvları arsında \displaystyle {{\text{R}}_{{\text{ip}}}}=\frac{{{{\text{ω}}_{{\text{ik}}}}}}{{{{\text{ω}}_{{\text{pk}}}}}}=\frac{{{{\text{ω}}_{{\text{1p}}}}-{{\text{ω}}_{{\text{1k}}}}}}{{{{\text{ω}}_{{\text{1i}}}}-{{\text{ω}}_{{\text{1k}}}}}}

R_jp = 1/R_pj olduğundan:

\displaystyle {{\text{R}}_{{\text{ip}}}}={{\text{R}}_{{\text{ij}}}}{{\text{R}}_{{\text{jp}}}}={{\left( {-1} \right)}^{1}}\frac{{{{T}_{\text{j}}}{{T}_{\text{i}}}}}{{{{T}_{\text{j}}}^{\prime }{{T}_{\text{p}}}}}=\frac{{{{\text{ω}}_{{\text{1p}}}}-{{\text{ω}}_{{\text{1k}}}}}}{{{{\text{ω}}_{{\text{1i}}}}-{{\text{ω}}_{{\text{1k}}}}}} 

olacaktır. Dikkat edilir ise, k kol uzvu sabit olduğunda, sistem basit dişli sistemidir ve dişli oranı yukarıda belirtildiği gibi olur (tahrik eden dişli, diş sayılarının çarpımının tahrik edilen dişlilerde diş sayılarının çarpımına oranı). Basit dişliye göre bir önemli fark bu tahrik edilen uzuv hızının tahrik eden uzuv hızına oranı olmayıp, tahrik edilen uzvun kola göre bağıl hızının tahrik eden uzvun kola göre bağıl hızına oranıdır.

Eğer bir dişli sistemde birden fazla kol ile taşınan faklı planet dişliler var ise bu durumda birleşik planet dişli sistemi vardır. Bu durumda her bir basit planet dişli sistemi için yukarıda gösterilmiş olan denklem yazılmalıdır. Genel olarak birleşik planet dişli sistemlerde ilk olarak planet dişli tanımlanmalıdır. Planet dişli ekseni sabit olmayan dişlidir. Bu planet dişli tanımlandıktan sonra, onu taşıyan ve planet dişliye döner mafsalla bağlı kolu tanımlamak gereklidir. Her kol bir basit planet dişli sistemidir. Kolu sabit kabul ederek dişli oranı ve bu orana eşit olan dişlilerin kola göre bağıl hızları oranı yazılabilir. Aşağıda verilmişm olan iki örnekle konu açıklanmaya çalışılacaktır.

Örnek:

Şekilde gösterilen dişli kutusunda giriş mili 3000 dev/dk dönerken çıkış milinin açısal hızını bulun.

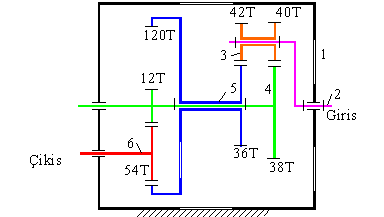
3 uzvu, sabit bir eksen etrafında dönmediğinden planet dişlidir. 2 uzvuna döner mafsal ile bağlı olduğundan 2 uzvu koldur. Kolun sabit olduğu var sayılır ise, 5 ile 4 uzvu arasında dişli oranı:

\displaystyle {{\text{R}}_{45}}={{\left( {-1} \right)}^{2}}\frac{{38\cdot 42}}{{40\cdot 36}}=\frac{{{{\text{n}}_{15}}-{{\text{n}}_{12}}}}{{{{\text{n}}_{14}}-{{\text{n}}_{12}}}}

veya

n₁₅ − n₁₂ = (133/120)(n₁₄ − n₁₂)

olacaktır. Bu denklemde n₁₂ bilinmekte, n₁₄ ve n₁₅ bilinmemektedir. Dişli kutusunun kalan kısmında bulunan 5, 4 ve 6 uzuvları sabit eksen etrafında döndüğünden basit dişli sistemlerini oluşturur. Bu durumda:

\displaystyle {{\text{R}}_{46}}={{\text{N}}_{46}}=-\frac{{12}}{{54}}=\frac{{{{\text{n}}_{16}}}}{{{{\text{n}}_{14}}}}     ve    \displaystyle {{\text{R}}_{56}}={{\text{N}}_{56}}=\frac{{120}}{{54}}=\frac{{{{\text{n}}_{16}}}}{{{{\text{n}}_{15}}}}

veya

n₁₄ = −(9/2)n₁₆     ;    n₁₅ = (9/20)n₁₆

olacaktır. Bu denklemler ilk planet dişli denklemine yerleştirilir ve n₁₆ için çözüm yapılır ise (n₁₂ = 3000 dev/dk):

n₁₅ = −(26/1305)n₁₂ ≅ −59.8 dev/dk      (giriş miline ters yöndedir)

Örnek:

Yüksek hız elde etmek için tasarlanmış bir dişli kutusu Şekilde görülmektedir. Giriş mili 1800 dev/dk. hızla dönmektedir. Çıkış milinin hızını ve giriş miline göre dönme yönünü bulunuz.

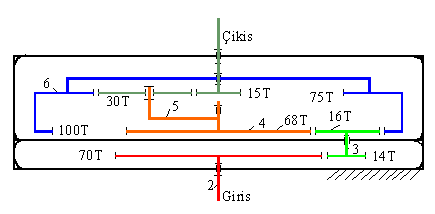
Dişli kutusunun ilk kısmında (2, 3, 4 ve 6 uzuvları) dişlilerin sabit eksenleri bulunmaktadır. Öyle ise:

\displaystyle {{\text{R}}_{24}}={{\left( {-1} \right)}^{2}}\frac{{70\cdot 16}}{{14\cdot 68}}=\frac{{{{\text{n}}_{14}}}}{{{{\text{n}}_{12}}}}     veya    n₁₄ = (20/17)n₁₂ ≅ 2117.65 dev/dk

\displaystyle {{\text{R}}_{26}}={{\left( {-1} \right)}^{1}}\frac{{70\cdot 16}}{{14\cdot 100}}=\frac{{{{\text{n}}_{16}}}}{{{{\text{n}}_{12}}}}    veya    n₁₆ = −(4/5)n₁₂ = 1440 dev/dk

Dişli kutusunun üst kısmında 5 uzvunun sabit bir ekseni olmadığına göre bu uzuv bir planet dişlidir. 4 uzvu planet dişliye döner mafsal ile bağlı olduğuna göre koldur. Bu durumda:

\displaystyle {{\text{R}}_{{67}}}={{\left( {-1} \right)}^{1}}\frac{{75}}{{15}}=\frac{{{{\text{n}}_{{17}}}-{{\text{n}}_{{14}}}}}{{{{\text{n}}_{{16}}}-{{\text{n}}_{{14}}}}}=-5

yazılabilir. n₁₇ için çözüm yapıldığında:

n₁₇ = 6n₁₄ − 5n₁₆ = (120/17 + 20/5)n₁₂ = (940/85)n₁₂ ≅ 19906 dev/dk     (dönüş yönü, giriş uzvu ile aynı yöndedir)

Genellikle tam sayı olan diş sayılarını en son hesap yapılana kadar tam sayı olarak korumak doğru olacaktır. Aksi takdirde küçük farklardan oluşan büyük bir dişli oranı ve küçük bir dişli oranı bulunamaz ve çok hatalı sonuçlar çıkabilir. Bu nedenle son etaba kadar hesap makinasının kullanılmaması önerilir.

Örnek:

Şekilde gösterilen dişli kutusunda 2 uzvu giriş uzvu olup 2000 dev/dk. açısal hızla dönmektedir. 6 uzvununun açısal hızını ve giriş uzvuna göre yönünü bulunuz.

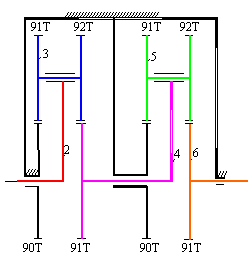
Dişli kutusu incelendiğinde, 3 ve 5 uzuvlarının sabit bir eksen etrafında dönmediği görülecektir. 3 uzvu 2 uzvuna 5 uzvuda 4 uzvuna döner mafsalla bağlı olduğundan, iki ayrı kol ve iki ayrı planet dişli gurubu bulunmaktadır. 2 uzvunu sabit alarak elde ettiğimiz sistem için diş oranını yazdığımızda:

\displaystyle {{\text{R}}_{{14}}}={{\left( {-1} \right)}^{2}}\frac{{90\cdot 92}}{{{{{91}}^{2}}}}=\frac{{{{\text{n}}_{{14}}}-{{\text{n}}_{{12}}}}}{{{{\text{n}}_{{11}}}-{{\text{n}}_{{12}}}}}

n₁₁ = 0 olduğundan:

n₁₄ = (1 − 90×92/91²)n₁₂ = n₁₂/8281

dir. Benzer bir şekilde 4 uzvunu sabit alarak elde ettiğimiz sistem için diş oranını yazdığımızda:

\displaystyle {{\text{R}}_{{16}}}={{\left( {-1} \right)}^{2}}\frac{{90\cdot 92}}{{{{{91}}^{2}}}}=\frac{{{{\text{n}}_{{16}}}-{{\text{n}}_{{14}}}}}{{{{\text{n}}_{{11}}}-{{\text{n}}_{{14}}}}}

olacaktır ve n₁₁ = 0 olduğundan:

n₁₆ = (1 − 90×92/91²)n₁₄ = n₁₄/8281 = n₁₂/68574961

n₁₂ = 2000 dev/dk olduğuna göre n₁₆ = 2.916516×10^-5 dev/dk = 0.041998 devir/gün veya 23.81 günde bir devir yapacaktır!!!!. Eğer yanılıp 90×92/91² ≅ 1 derseniz, 6 uzvunun hareketsiz olduğu sonucuna varabilirsiniz.