6.3 Konik Dişli Kullanan Dişli Kutuları
Hareket iletimi paralel olmayan miller arasında yapılacak ise, genellikle konik dişliler kullanılır. Kinematik açıdan konik dişliler birbiri üzerinde yuvarlanan iki koniğe eşdeğerdir. Konik dişliler basit veya planet dişli sistemlerde kullanılabilirler. Kinematik analizleri, iki fark dışında düz dişliler ile oluşturulan dişli sistemlerle aynıdır. Birinci önemli fark burada anlatılacak olan yöntem ekseni sabit olmayan planet dişlilerin açısal hızlarının hesaplanmasında kullanılamaz, çünkü uzayda paralel olmayan eksenler etrafında dönemler toplanamaz. İkinci fark ise, düz dişlilerde kullanılan açısal yön belirleme yöntemi konik dişliler için uygulanamaz.
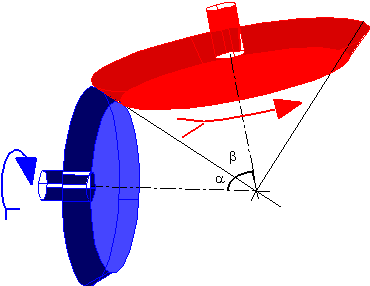
Şekilde birbirleri ile dişli çift oluşturan iki konik dişli görülmektedir. Eksenler arasında açı θ dır. P noktasında sadece yuvarlanma olduğundan, iki uzuv üzerinde hızlar eşit olacaktır:
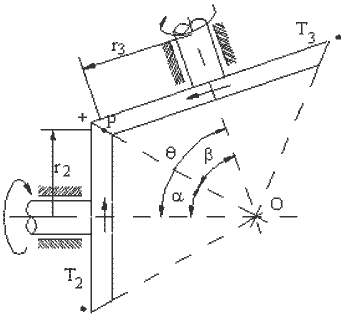
θ = α + β
ve
\displaystyle \frac{{{{\text{ω}}_{{13}}}}}{{{{\text{ω}}_{{12}}}}}=\frac{{{\text{r}_{2}}}}{{{\text{r}_{3}}}}=\frac{{{\text{T}_{2}}}}{{{\text{T}_{3}}}}=\frac{{{{\text{r}}_{2}}/\text{OP}}}{{{{\text{r}}_{3}}/\text{OP}}}=\frac{{\sin \text{α}}}{{\sin \text{β}}}={{\text{R}}_{{23}}}
dür. Uzuvların dönme yönünü belirlemek için yine P noktasında iki koninin hızının aynı olması gerektiğini not edelim. Eğer 2 uzvu O noktasından baktığımızda saat yelkovanı yönünde dönüyor ise, 3 uzvu O noktasından baktığımızda saat yelkovanına ters yönde dönecektir. Bunu belirlemek için dönen bir ok düşünelim 2 uzvu saat yelkovanı yönünde döndüğünden bu ok şekilde görülen kesit düzlemine P noktasından (koninin üst kısmından) girecek, koninin alt kısmından ise dışarı çıkacaktır. Bir oka arkadan baktığımızda “+” önden baktığımızda ise “•” görürüz. Öyle ise 2 uzvu için ok şekilde gösterildiği gibi yukarıda + aşağıda ise • görülecektir. 3 uzvunda ise koninin P tarafında “+” yani okun içeriye doğru olduğu bilindiğine göre, diğer tarafta “•” yani okun kağıdı delerek çıkması gerekir. O noktasından baktığımızda ise 3 uzvu saat yelkovanı yönüne ters dönüyor görülecektir. Bu yöntem ile uzuvların dönme yönleri belirlenebilir.
Örnek:
Şekilde gösterilen birleşik basit dişli zincirinde 4 uzvunun 2 uzvuna göre açısal hız oranını (R24 = N24) bulunuz.
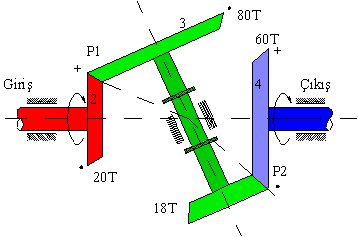
\displaystyle {{\text{R}}_{{23}}}=\frac{{80}}{{20}}=\frac{{{\text{ω}_{{13}}}}}{{{\text{ω}_{{12}}}}} ve \displaystyle {{\text{R}}_{{34}}}=\frac{{18}}{{60}}=\frac{{{\text{ω}_{{14}}}}}{{{\text{ω}_{{13}}}}}
veya
\displaystyle {{\text{R}}_{{24}}}=\frac{{{\text{ω}_{{14}}}}}{{{\text{ω}_{{12}}}}}=\frac{{20\cdot 18}}{{80\cdot 60}}=\frac{3}{40}=\frac{{\text{Tahrik eden dişli diş sayıları çarpımı}}}{{\text{Tahrik edilen dişli diş sayıları çarpımı}}}
0larak bulunur. Ancak bu hesaplamada düz dişlilerde olduğu gibi yön göz önüne alınmamıştır. 2 uzvunun her hangi bir yönde döndüğünü kabul edelim. Örneğin sağdan baktığımızda 2 uzvu saat yelkovanı yönünde dönüyor olsun. Bu dönme yönünü gösteren ok dişlinin üst tarafından kağıttan dışarı çıkacak, alt tarafından ise içeri doğru girecektir. Buna uygun olarak ilk işaretimizi koyduğumuzda, 3 uzvunun dönme yönü, P1 noktasında okun içeri doğru girmesi, P2 noktasında ise okun dışarı doğru çıkması ile neticelenir. 4 uzvu ise bu durumda P2 noktasında ok dışarı çıkıyor ise, koninin üst tarafında ok içeri doğru girecektir. Öyle ise, 2 ve 4 uzuvları aynı yönde dönmektedirler. Şekilde görüldüğü gibi (+) ve (•) sembollerini sıra ile bu kurala uygun yerleştirdiğimizde uzuvların yönleri belirlenmiş olur. Öyle ise:
\displaystyle {{\text{R}}_{{24}}}=\frac{{{\text{ω}_{{14}}}}}{{{\text{ω}_{{12}}}}}=\frac{{20\cdot 18}}{{80\cdot 60}}=+\frac{3}{40}=+0.075
Eğer konik dişliler planet dişlilerde kullanılıyor ise, sabit eksenli dişliler arasında dişli oranını, hızların kola göre bağıl hızlarına eşitliyerek bulmamız mümkündür. Ancak planet dişlinin hızını bu yöntemle bulmak doğru değildir.
Örnek:
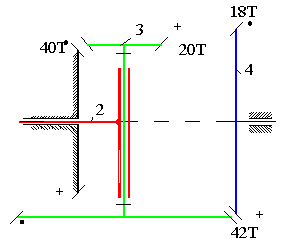
Şekilde gösterilen dişli sisteminde 2 ve 4 uzuvları arasında açısal hız oranlarını ve bu açısal hızların birbirlerine göre yönünü bulmak istiyoruz. Dikkat edilir ise 3 uzvu planet dişlidir ve 2 uzvuna döner mafsalla bağlı olduğundan 2 uzvu koldur. 2 uzvunu sabit tuttuğumuzda 1, 3 ve 4 uzuvları arasında elde edilen basit dişli sistem için dişli oranı:
\displaystyle {{\text{R}}_{{14}}}=\frac{{40\cdot 42}}{{20\cdot 18}}=\frac{14}{3}=\frac{{{{\text{n}}_{{14}}}-{{\text{n}}_{{12}}}}}{{{{\text{n}}_{{11}}}-{{\text{n}}_{{12}}}}}
Bu basit dişli sistem için (2 uzvu sabit varsayıldığında) dönme yönleri dönme okunun yönüne uygun olacak şekilde işaretlenerek belirlendiğinde, 1 ve 4 uzuvlarının aynı yönde döndükleri görülmektedir. n11 = 0 olduğundan n14 için:
n14 = (1 − 14/3)n12
veya
N24 = n14/n12 = −11/3
elde edilir. Dikkat edilir ise, sonuçta 2 ve 4 uzuvları birbirlerine ters yönde dönmektedir.
Örnek:
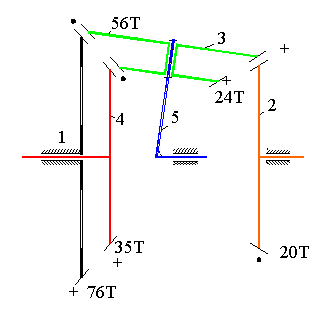
Şekilde “Humpage’in konik dişli diferansiyeli” olarak adlandırılan sistem görülmektedir. N24 hız oranını bulmamız istenmektedir.
2, 3 ve 1 uzvundan oluşan zincir incelendiğinde, 3 uzvu planet dişli ve 5 uzvu koldur. Öyle ise:
\displaystyle {{\text{R}}_{12}}=\frac{{{{\text{n}}_{12}}-{{\text{n}}_{15}}}}{{{{\text{n}}_{11}}-{{\text{n}}_{15}}}}=-\frac{{76\cdot 56}}{{56\cdot 20}}=-\frac{19}{5}
n11 = 0 olduğundan n15 = (5/24)n12
1, 3 ve 4 uzvundan oluşan zincirde 3 uzvu planet ve 5 uzvu onu taşıyan koldur. Öyle ise:
\displaystyle {{\text{R}}_{14}}=\frac{{{{\text{n}}_{14}}-{{\text{n}}_{15}}}}{{{{\text{n}}_{11}}-{{\text{n}}_{15}}}}=+\frac{{76\cdot 24}}{{56\cdot 35}}=+\frac{228}{245}
yazılabilir. n11 = 0 olduğundan n14 = (1 − 228/245)n15 = (17/245)n15 = (17/1176)n12 veya N24 = n14/n12 = 0.0145 olacaktır.
Bir diferansiyel nasıl çalışır?
Tüm arabalarda viraj alırken dışarda bulunan teker daha fazla mesafe kat edeceğinden daha içerde bulunan tekere göre daha hızlı dönecektir. Tahrik edilen tekerler aynı motor tarafından tahrik edildiğinden eğer tek serbestlik dereceli bir mekanizma kullanılır ise, her iki teker aynı miktar döndürüleceğinden dolayı, araç kayar. Bunu önlemek için tekerlekler diferansiyel olarak adlandırılan iki serbestlik dereceli bir konik planet dişli sistemi ile tahrik edilirler.
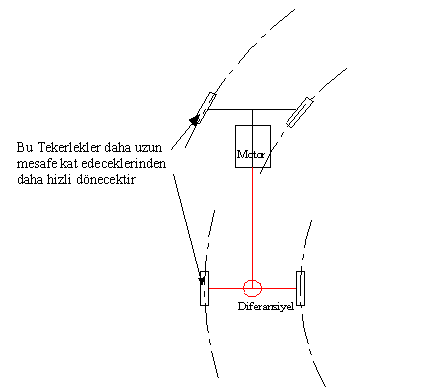
Viraj sırasında teker dönmesi
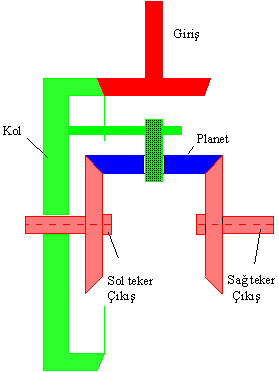
Dişli kutusundan çıkan milin çevirdiği giriş dişlisi planet dişli sistemde kolu çevirmektedir. Kola döner mafsal ile planet dişli bağlıdır (genellikle 3 veya 4 planet dişli bulunur). Sağ ve sol teker dişlileri sabit ve çakışan bir eksende dönmektedir. Sistem görüldüğü şekilde iki serbestlik derecesine sahiptir.
Eğer iki tekere gelen yük eşit ise tüm sistem, kolun dönme açısı hızında birlikte döner.
Eğer tekerlerden birine etki eden yük diğer tekere gelen yüke göre çok fazla ise, bir teker sabit durur ve diğer teker iki misli hız ile döner. Virajlarda iç teker dış tekere göre daha fazla sürtünme kuvveti ile karşılacağından iç teker dış tekere göre daha az dönecektir.
Sistem iki serbestlik dereceli olduğundan uygulamada tekerleklerin dönme miktarı etki eden dış kuvvetlere ve sistemin dinamiğine bağlı olacaktır.
Benzer diferansiyel sistemi bir engele çarptığında yön değiştiren oyuncak arabalarda görürsünüz.
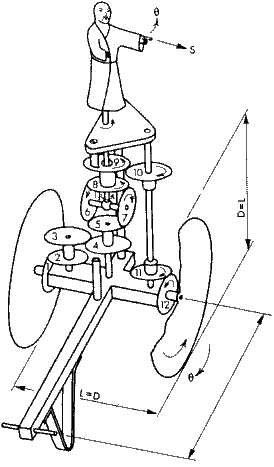
Güneyi Gösteren Savaşcı (Milattan önce 2600 yıllarında):
Aşağıda görülen araba Çinliler tarafından Gobi çölünü geçerken kullanılan öküzler tarafından çekilen bir arabanın temsili resmidir. Dişliler görüldüğü gibi zamanında tahta pimlerden yapılmıştır. Ancak o devirdede planet dişli sistemi ve diferansiyel kavramını bildikleri görülmektedir. Araba düz giderken savaşcının yönü değişmemekte, araç sağa veya sola döndüğünde, aynı açıda savaşcı arabaya göre ters yönde dönmekte ve yere göre hiç bir açısal dönme yapmamış olmaktadır. Bu şekilde savaşcı yola başlarken gösterdiği yönü devamlı göstermektedir.