7.5 Dört Çubuk ve Krank-Biyel Mekanizmaları Eşlenikleri: Robert- Çebişev Teoremi
Bir dört-çubuk veya bir krank-biyel mekanizmasında temel sorunumuz bir biyel eğrisi ise, aynı biyel eğrisini çizen başka dört-çubuk veya krank-biyel meka-nizması boyutları bulmamız mümkündür. Aynı biyel eğrisini veren farklı uzuv boyutlarına sahip dört çubuk mekanizmalarına birbirlerinin eşleniği diyeceğiz. Bu eşleniklerin bulunması için geçerli kural Robert-Çebişev teoremi ile verilmektedir:
Robert-Çebişev Teoremi
Aynı biyel eğrisini çizen değişik uzuv boyutları olan üç değişik dört-çubuk mekanizması vardır.
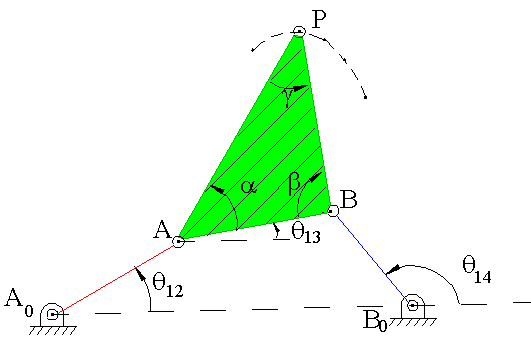
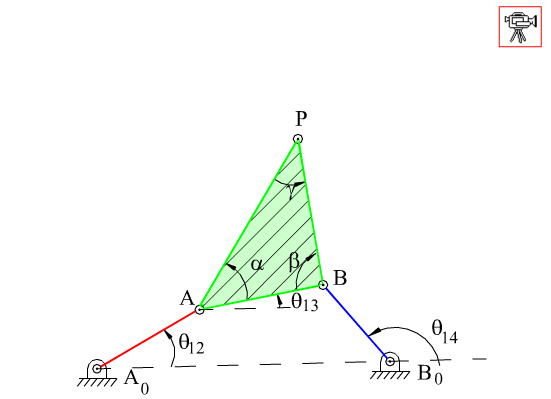
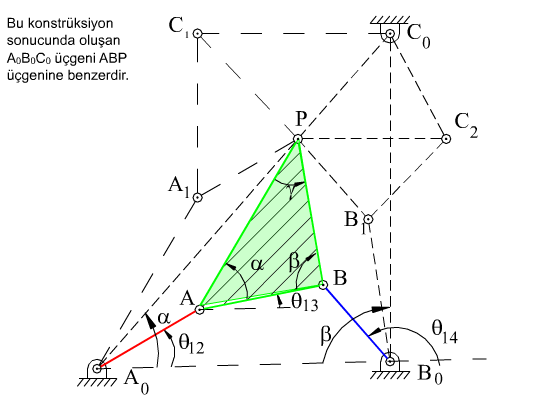
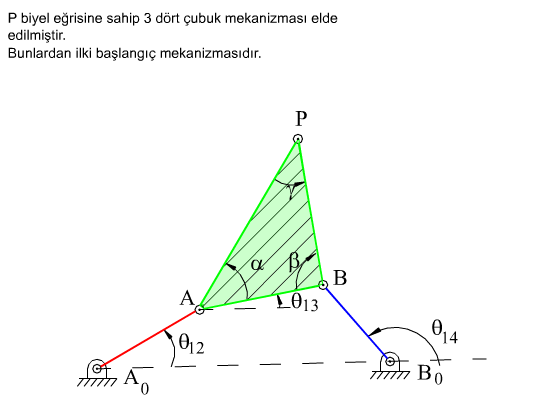
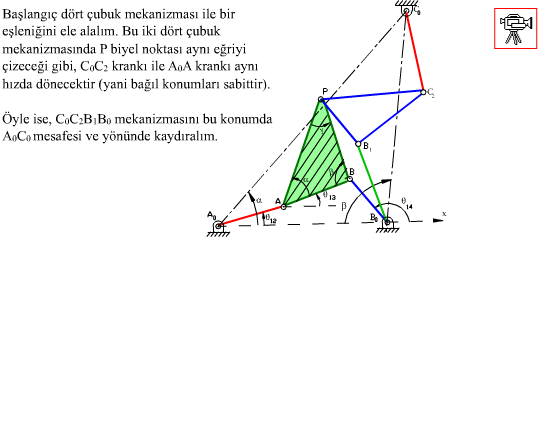
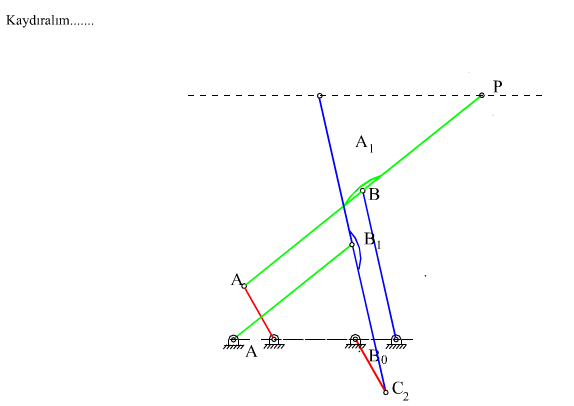
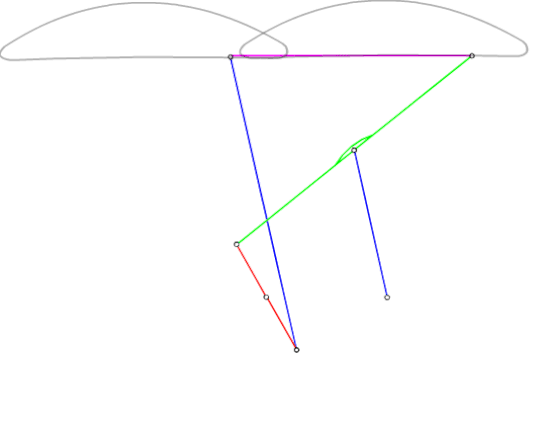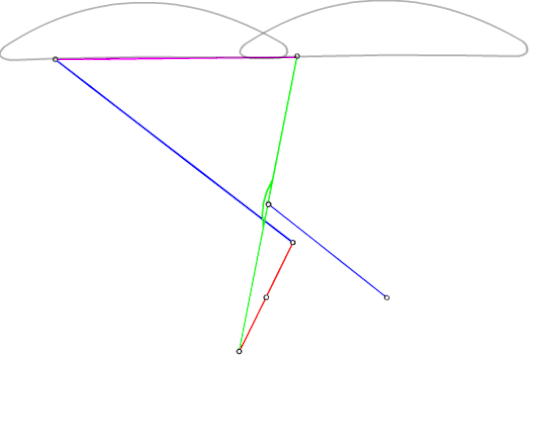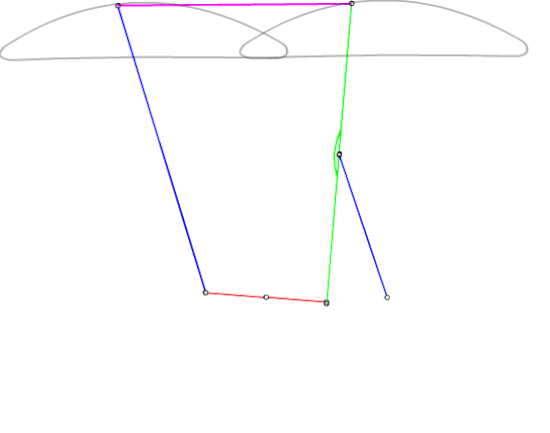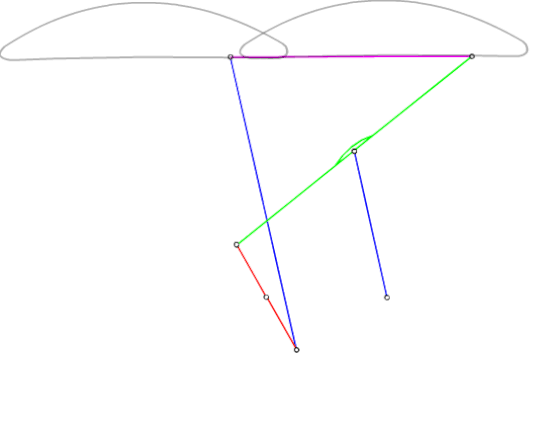
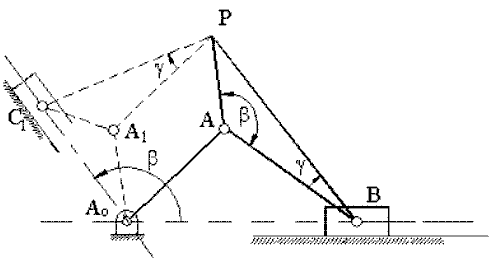
Şekilde gösterilen dört-çubuk mekanizmasını ele alalım (|A0B0| = a1, |A0A| = a2, |AB| = a3, |B0B| = a4, |AP| = b3, |BP| = c3 tür). P biyel noktası gösterilen bir biyel eğrisini çizmektedir. Bu mekanizma için devre kapalılık denklemi:
| a2eiθ12 + a3eiθ13 = a1 + a4eiθ14 | (1) |
P biyel noktasının her hangi θ12 açısı için kompleks konum vektörü:
| ZP = a2eiθ12 + b3ei(θ13 + α) | (2) |
veya
| ZP = a1 + a4eiθ14 + c3ei(θ13 + π − β) | (3) |
ile tanımlanır. Dikkat edilir ise (2) ve (3) denklemlerinde bulunan bağımlı konum değişkenleri θ13 ve θ14 her krank açısı θ12 için (1) numaralı devre kapalılık denkleminden 3. kısımda açıklandığı gibi çözülür.
Eşleniklerin bulunması:
Aynı biyel eğrisini çizen dört-çubuk mekanizmaları:
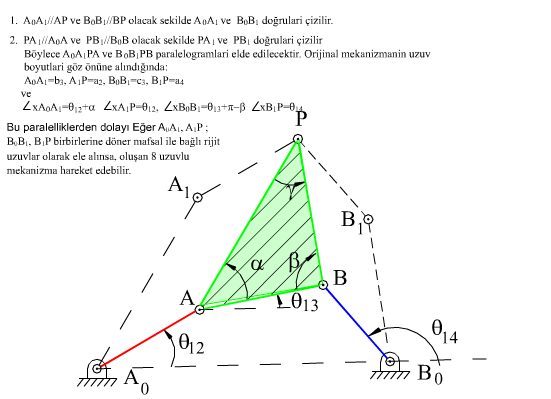
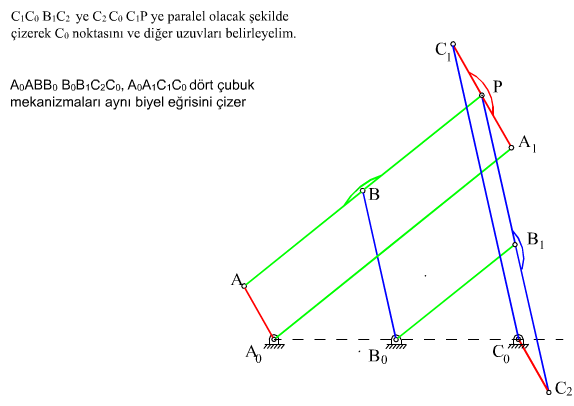
A0ABB0 (P, AB uzvu üzerinde)
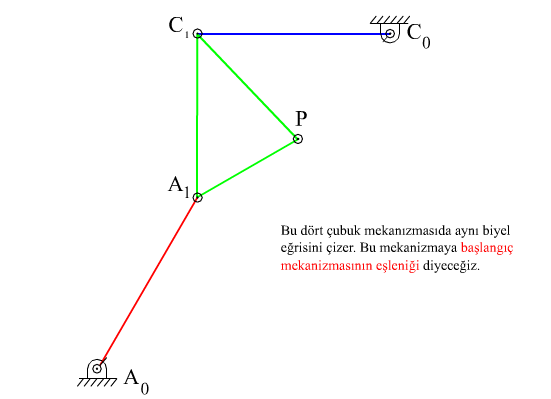
C0C1A1A0 (P, C1A1 uzvu üzerinde)
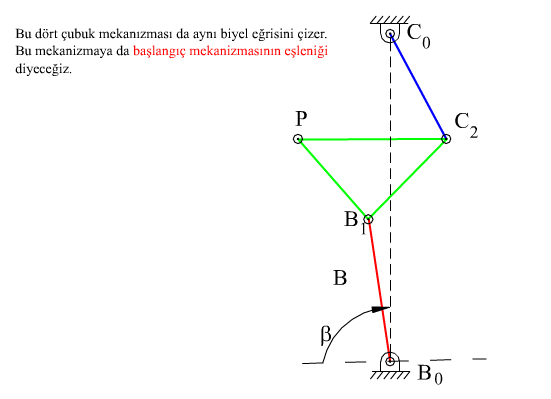
C0C2B1B0 (P, C1B1 uzvu üzerinde)
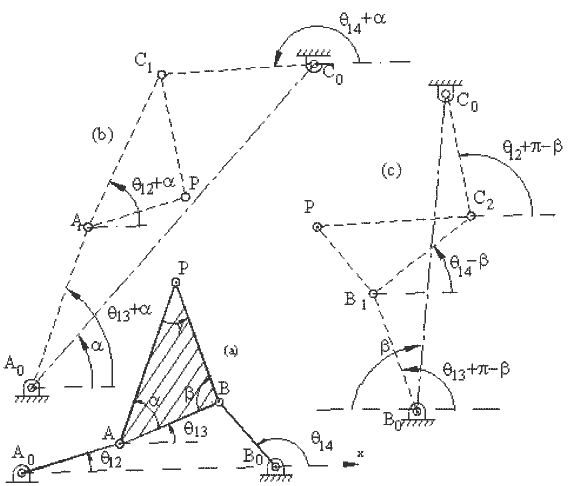
Şimdi, C0 noktasının konumu :
A0C0 = A0A1 + A1C1 + C1C0
veya
A0C0 = A0B0 + B0B1 + B1C2 + C2C0
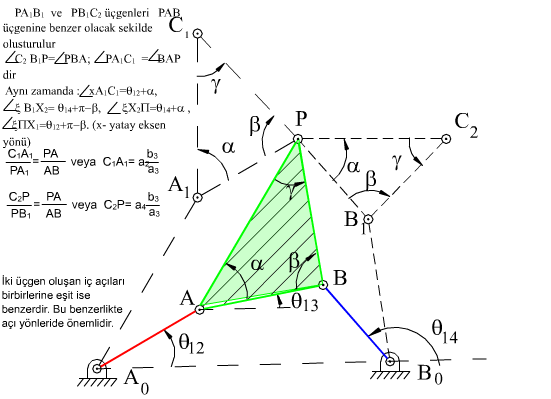
şeklinde yazılabilir. Kompleks sayılar kullanarak ve yukarıda elde edilmiş olan açısal ve boyutsal eşitliklikleri göz önüne alarak her iki denklem:
| A0C0 = b3ei(θ13 + α) + (a2b3/a3)ei(θ12 + α) − (a4b3/a3)ei(θ14 + α) | (4) |
veya
| A0C0 = a1 + c3ei(θ13 + π − β) + (a2c3/a3)ei(θ12 + π − β) + (a4c3/a3)ei(θ14 − β) | (5) |
şeklinde yazılabilir. Elde edilen (4) denkleminde sağ tarafta bulunan terimleri b3/a3eiα ve (5) denkleminde sağ tarafta bulunan terimleri c3/a3ei(π − β) parantezine alır isek:
| A0C0 = b3/a3eiα(a2eiθ12 + a3eiθ13 − a4eiθ14) | (6) |
veya
| A0C0 = a1 + c3/a3ei(π − β)(a2eiθ12 + a3eiθ13 − a4eiθ14) | (7) |
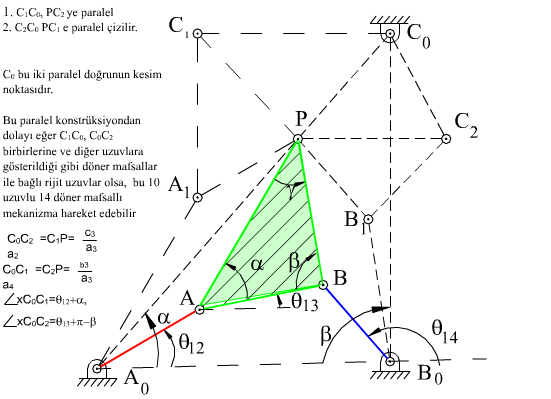
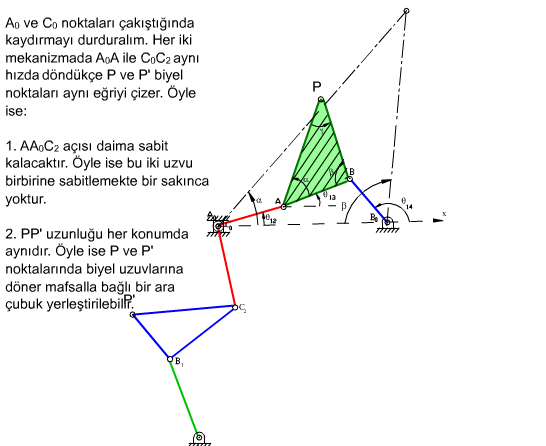
olacaktır. Denklem (1) göz önüne alındığında parantez içinde bulunan terimlerin toplamı a1 değerine eşittir ve C0 sabit bir nokta olacaktır, diğer iki dört-çubuk mekanizmasının devre kapalılık denklemleri, eğer ilk mekanizmanın devre kapalılık denklemi (1) sağlanıyor ise, sağlanmış olacaktır. C0 sabit noktası konum vektörü a1b3/a3eiα, θ12, θ13 ve θ14 denklem (1) e göre ilintili olmak üzere, her üç dört çubuk mekanizmasının P biyel noktası aynı konumda olacak ve aynı biyel eğrisini çizecektir. Böylece Robert-Çebişev teoremi ispat edilmiş olur.
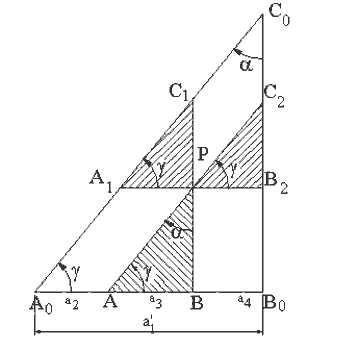
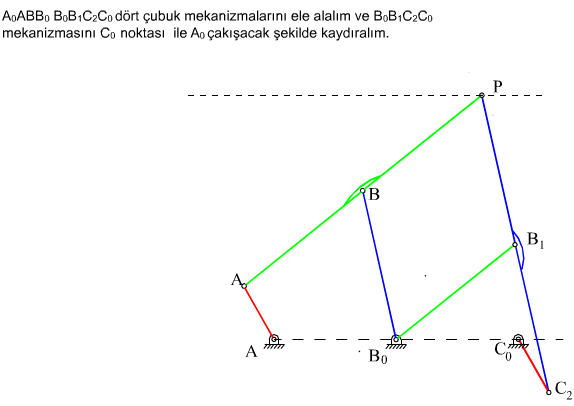
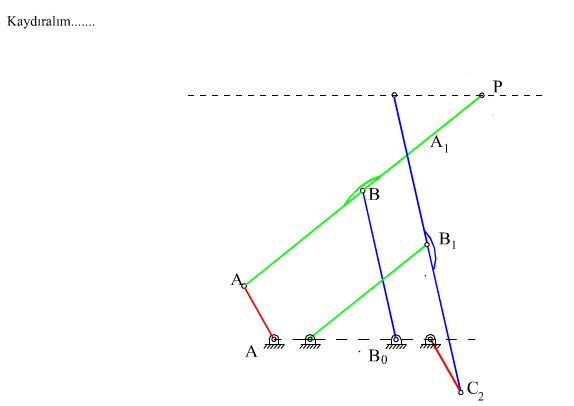
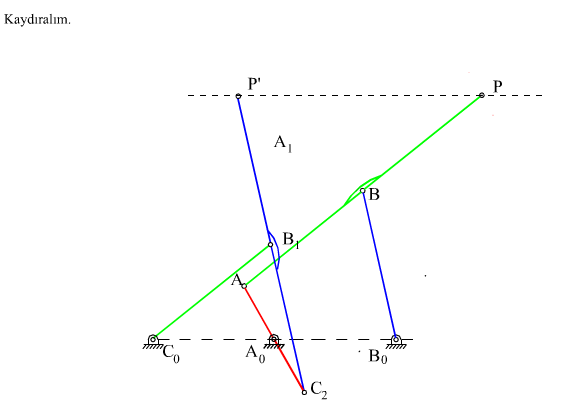
Gösterilen yöntem diğer dört-çubuk mekanizmalarının hem boyutlarını ve hemde birbirlerine göre konumlarını belirlemektedir. Sadece uzuv boyutlarını bulmak için daha basit bir yöntem kullanılabilir. Bunun için ele alınan dört-çubuk mekanizmasında sabit uzuv boyutunu ihmal ederek A0ABB0 noktaları bir doğru olacak şekilde hareketli uzuvları uzatalım. Robert-Çebişev teoremi böyle bir (hareketsiz) mekanizma içinde geçerli olduğundan aynı grafik kurallar kullanılarak yapılabilir ancak bu durumda yeni sabit uzuv boyutu: a′1 = a2 + a3 + a4 dir. Sonuç yukarıda da görülmektedir. Yeni C0 noktasının konumu ise:
A0C0 = a1b3/a3eiα = a1 + a1c3/a3ei(π − β) , |A0C0| = a1b3/a3 , |B0C0| = a1c3/a3
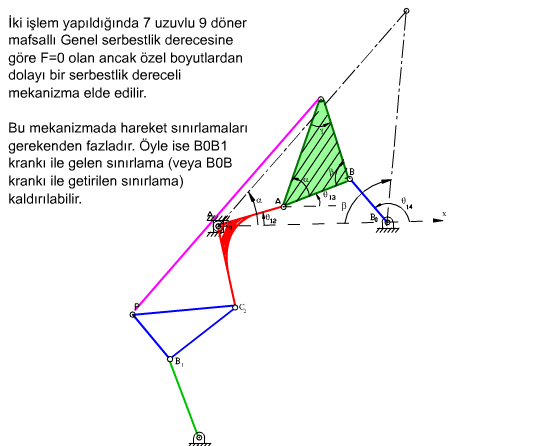
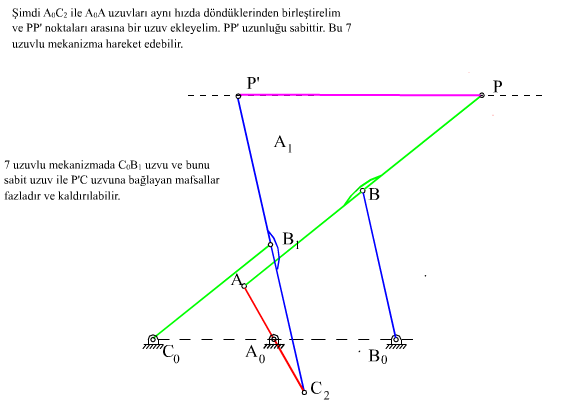
olacak şekilde belirlenir. Üç eşlenik dört-çubuk mekanizması elde edildikten sonra, dikkat edilir ise, P noktasında bir döner mafsal olduğu durumda her üç dört-çubuk mekanizması döner mafsallarla birbirlerine bağlı olduğu halde, paralelogram yapıdan dolayı yine hareket edeceklerdir. Şekilde elde edilen mekanizma 10 uzuvlu ve 14 döner mafsallı (6 tekli, 4 çiftli döner mafsal) olup serbestlik derecesi denklemine göre serbestlik derecesi −1 olduğu halde, hareket edebilir. Mekanizma daimi kritik haldedir.
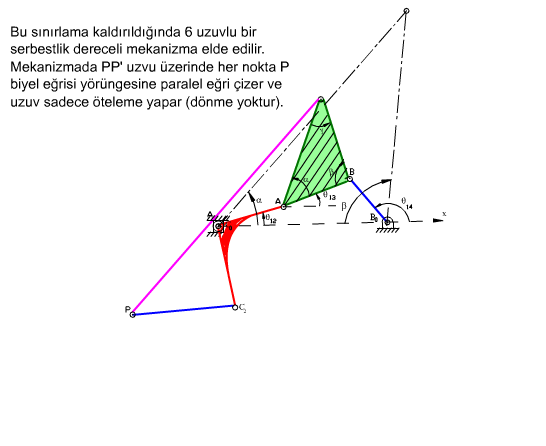
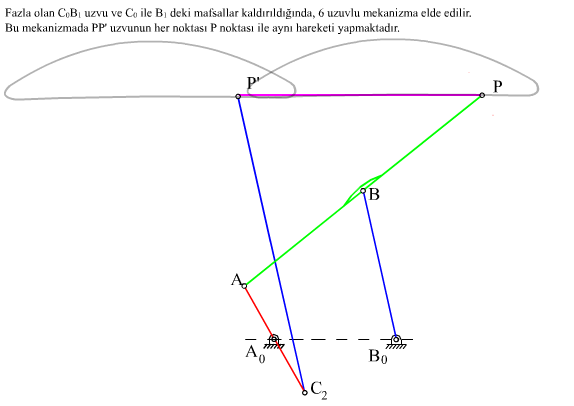
Eşlenik mekanizmalar, uygun bir biyel eğrisi elde edildiğinde tasarımcaya üç değişik boyuta sahip dört-çubuk mekanizması olanağı vermesi açısından önemlidir. Eşlenik mekanizmaların bir başka kullanım şekli ise, bu mekanizmalardan yararlanarak bir uzvun her noktası aynı biyel eğrisini çizerek öteleme yapan altı uzuvlu bir mekanizmanın tasarımının yapılabilmesidir. Bu mekanizmanın bir uzvu sadece öteleme yapacak, bu uzuv üzerinde alınan herhangi bir doğru ilk konumuna daima paralel kalacaktır.
Örnek:
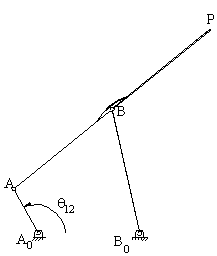
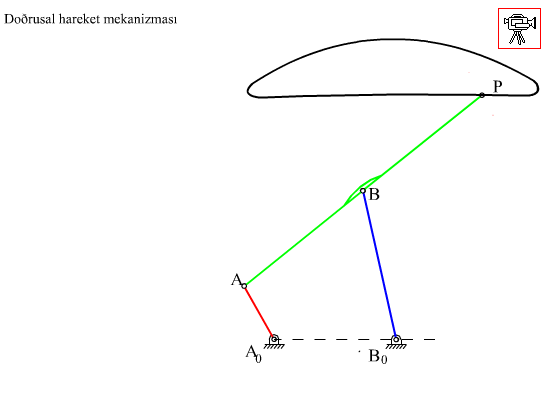
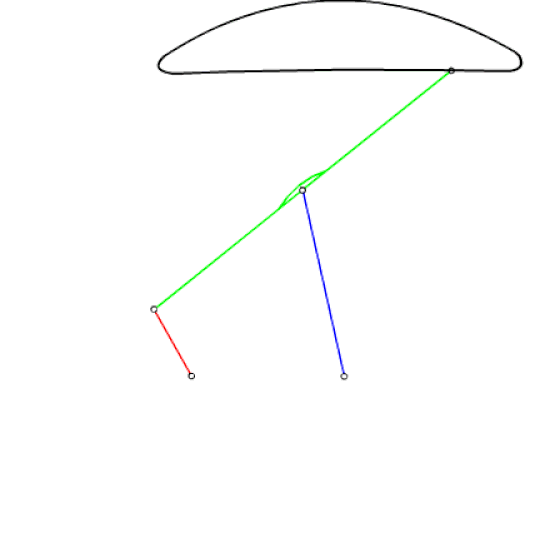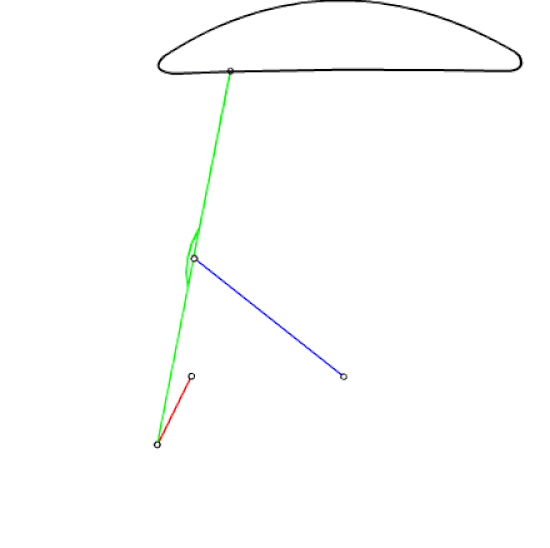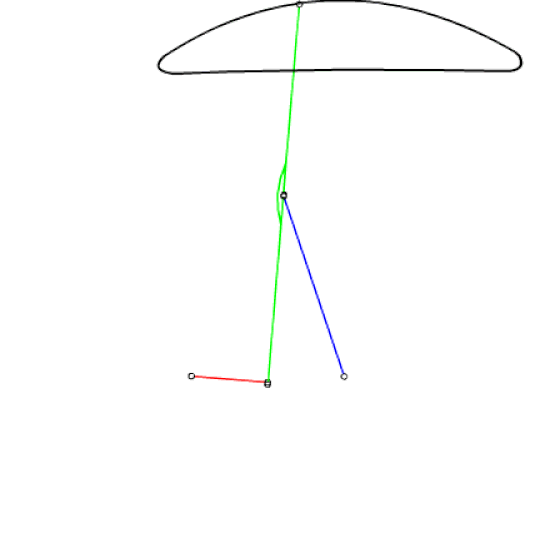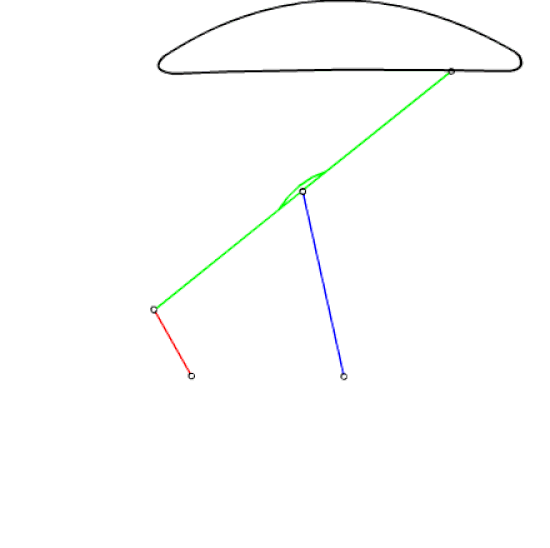
Şekilde görülmekte olan mekanizma Çebişev lambda mekanizması veya Hoecken doğrusal hareket mekanizması olarak bilinmektedir. P biyel noktası krankın belirli bir dönme aralığında yaklaşık olarak bir doğru çizer. Uzuv boyutları oranı: |AB| = |BP| = |B0B| = 2.5|A0A|, |A0B0| = 2|A0A| dır. Bu mekanizmadan yola çıkarak bir uzvu yaklaşık olarak doğrusal öteleme yapan altı uzuvlu bir mekanizma elde etmek istiyoruz. yöntem aşağıda açıklanmaktadır.
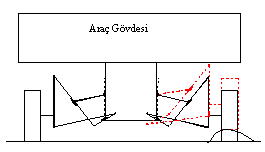
Elde edilmiş olan bu 6 uzuvlu mekanizma arazide gidecek bir aracın suspansiyon sıstemi olarak kullanılabilir. Bu durumda her hangi bir teker bir çukura veya tümseğe geldiğinde, diğer tekerleri etkilemeden, yere dik olacak şekilde yukarı-aşağı hareket edebilecektir.
Krank biyel mekanizması eşleniği
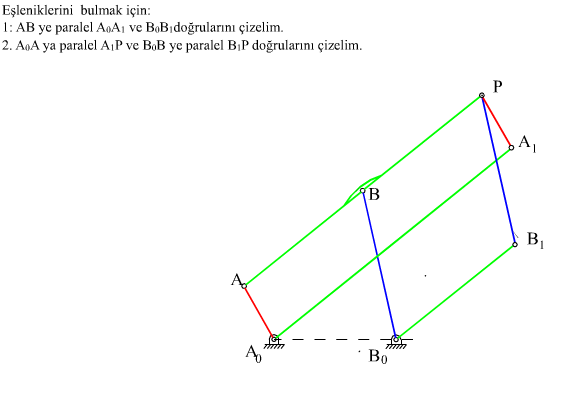
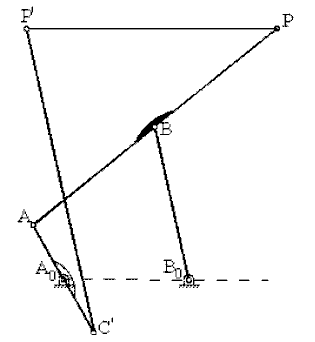
Krank biyel mekanizmalarında aynı biyel eğrisini çizen iki değişik krank-biyel mekanizması boyutu bulunmaktadır. Verilen bir krank-biyel mekanizmasının eşleniğini bulmak için geometrik olarak:
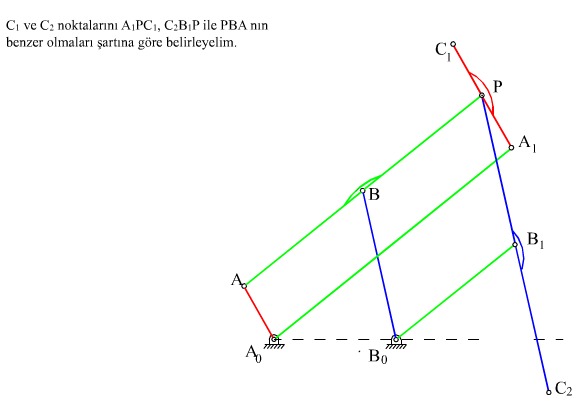
- PA1//AA0 ve A0A1//PA olacak şekilde PA1 ve A0A1doğrularını çizip A1 noktasını belirleyin.
- ΔPA1C1 üçgenini ΔPAB üçgenine benzer olacak şekilde çizin (∠A1PC1 = ∠ABP olacaktır).
Dört çubuk mekanizmasında olduğu gibi, A0AB bir doğru üzerinde olacak şekilde yerleştirilerek aynı işlem yapılabilir. Bu durumda eşlenik uzuv boyutları daha kolay elde edilirse de uzuvların birbirlerine göre konumları elde edilemez.
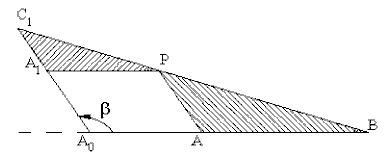
Tasarımcının bir uygulamada temel hedefi bir biyel eğrisi ise, elde edilen eşlenik mekanizmaları ilk kullandığı mekanizmanın yerine kullanabilir. Kullanacağı bu mekanizmanın uzuv boyutları oranı veya bağlama açısı daha iyi olabileceği gibi, mekanizmanın makinada yerleştirilmesi daha kolay olabilir.