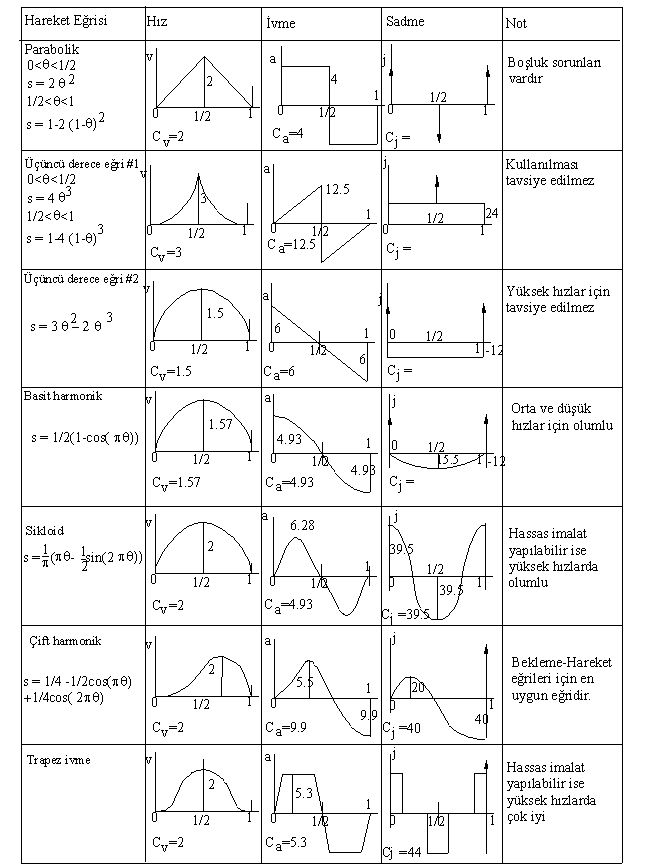
Hareket eğrilerinin “Normalizasyonu”

Yukarıda verilen eğrileri birbirleri ile karşılaştırmak için bu eğrilerin “normalize” edilmesi gerekmektedir. Normalizasyon hareket denklemlerinde H, ω ve β değerlerinin

ω = 1 rad/s

H = 1 birim

β = 1 radyan

olarak alınması ile yapılır. Karşılaştırmak için şekilde çeşitli eğrilerin hız, ivme ve ivme değişim diyagramları gösterilmiştir. C_v, C_a ve C_j, normalize edilmiş hareket eğrilerinin maksimum hız, ivme ve ivme değişim değerleridir. Her hangi H, ω ve β değeri için maximum hız, ivme ve ivme değişim değeri (sadme) bulunmak istendiğinde:

v_max = C_vHω/β

a_max = C_aHω²/β²

j_max = C_jHω³/β³

olarak elde edilir. Her hangi bir H yükselme ve b kam dönme hareketi için yazmak istediğimizde, normalize edilmiş eğri denklemini H ile çarpmak ve θ açısı yerine θ/β yerleştirmek yeterlidir. Örneğin normalize edilmiş üçüncü derece hareket eğrisi (#2):

s = 3θ² + 2θ²

olarak verildiğinden, denklemi H ile çarpar θ açısı yerine θ/β yerleştirir isek:

s = H[3(θ/β)² − 2(θ/β)³]

veya

s = H(θ/β)²(3 − 2θ/β)

olacaktır. Bu eğrinin maksimum hız ve ivme değerleri: v_max = 1.5Hω/β, a_max = 6H(ω/β)² dir.

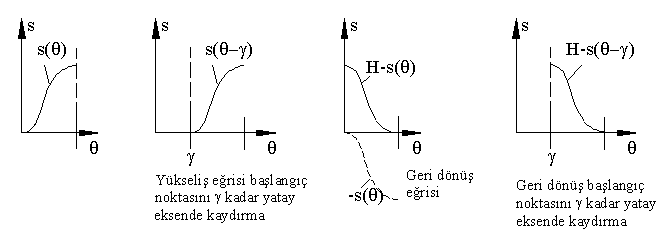
θ = 0 dan başlayan ve θ = β da s = H kadar yükselen bu eğriler, merkez değiştirme ve H yüksekliğinden çıkarma yapılarak geri dönüş eğrisi olarak da kullanılabilir. Bu işlemler şekilde gösterilmektedir. Örneğin eğrinin θ = γ açısında yükselmeye başlaması için eğri denkleminde her q terimi yerine (θ − γ) terimi yerleştirebilir, bu eğriyi geri dönüş eğrisi yapmak için ise, bu yükseliş eğrisi denklemini (s(θ)), H değerinden çıkarmak gereklidir. f(θ) = H − s(θ) denklemi θ = 0 da başlayan geri dönüş denklemidir. f(θ) = H − s(θ − γ) ise θ = γ da başlayan geri dönüş denklemi olur ). Çift harmonik dışında tüm eğriler simetrik olduğundan elde edilen eğriler yine istenilen özelliklere sahip olacaktır.